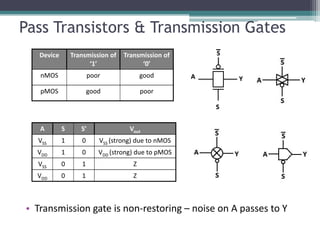
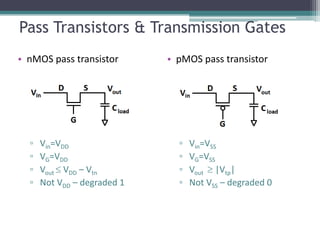
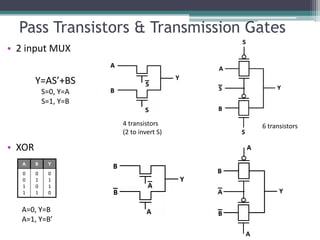
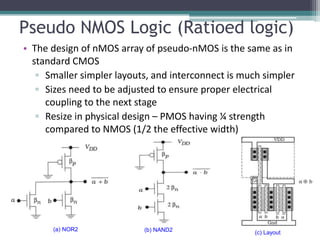
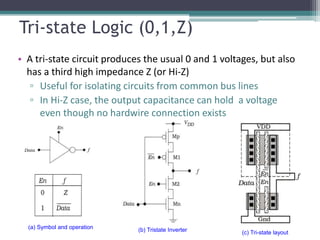
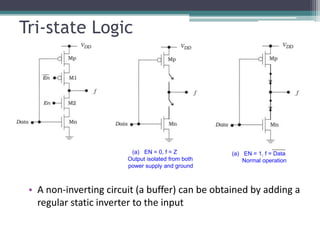
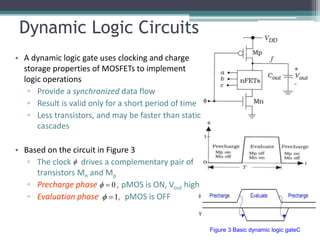
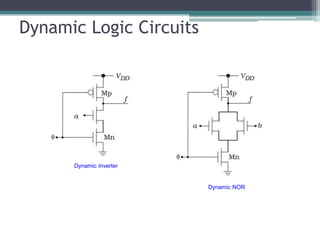
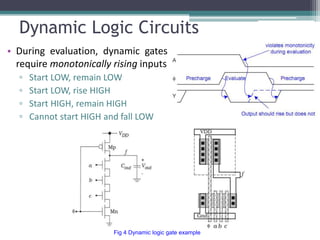
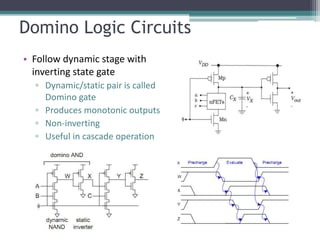
The document outlines various VLSI combinational logic circuit design techniques, including pass transistors, transmission gates, pseudo NMOS logic, tri-state logic, dynamic logic, and domino logic. Each technique is described in terms of its operational characteristics, circuit configurations, and advantages, such as reduced transistor count and improved isolation in state circuits. Additionally, it discusses the implications of dynamic logic designs and issues like charge sharing and monotonicity in outputs.

1. Combinational Logic
VLSI Circuit Design

2. Outline
• Pass Transistors
• Transmission Gates
• Pseudo nMOS Logic
• Tri-state Logic
• Dynamic Logic
• Domino Logic

3. Pass Transistors & Transmission Gates
• Transmission gate is non-restoring – noise on A passes to Y
Device Transmission of
‘1’
Transmission of
‘0’
nMOS poor good
pMOS good poor
A S S’ Vout
VSS 1 0 VSS (strong) due to nMOS
VDD 1 0 VDD (strong) due to pMOS
VSS 0 1 Z
VDD 0 1 Z

4. Pass Transistors & Transmission Gates
• nMOS pass transistor
▫ Vin=VDD
▫ VG=VDD
▫ Vout  VDD – Vtn
▫ Not VDD – degraded 1
• pMOS pass transistor
▫ Vin=VSS
▫ VG=VSS
▫ Vout  |Vtp|
▫ Not VSS – degraded 0

5. Pass Transistors & Transmission Gates
• 2 input MUX
• XOR
A B Y
0
0
1
1
0
1
0
1
0
1
1
0
4 transistors
(2 to invert S)
6 transistors
A=0, Y=B
A=1, Y=B’
Y=AS’+BS
S=0, Y=A
S=1, Y=B

6. Pass Transistors & Transmission Gates
• AND
• OR
A B Y
0
0
1
1
0
1
0
1
0
0
0
1
A B Y
0
0
1
1
0
1
0
1
0
1
1
1
A=0, Y=A
A=1, Y=B
A=0, Y=B
A=1, Y=A

7. Pseudo NMOS Logic (Ratioed logic)
• Single PMOS in pull-up network – gate
connected to VSS
• PMOS always in ON state
• Less transistors than CMOS, smaller area
• For N inputs, only requires (N+1) MOS
• NMOS logic array acts as a large switch
between the output f and ground
• However, since the PMOS is always biased
on, VOL can never achieve the ideal value of
0 V – static power dissipation
• A simple inverter using pseudo-NMOS is
shown: Figure 2
Fig 2 Pseudo-nMOS inverter
Fig 1 General structure of a
pseudo-nMOS logic gate

8. Pseudo NMOS Logic (Ratioed logic)
• The design of nMOS array of pseudo-nMOS is the same as in
standard CMOS
▫ Smaller simpler layouts, and interconnect is much simpler
▫ Sizes need to be adjusted to ensure proper electrical
coupling to the next stage
▫ Resize in physical design – PMOS having ¼ strength
compared to NMOS (1/2 the effective width)
(a) NOR2 (b) NAND2 (c) Layout

9. Tri-state Logic (0,1,Z)
• A tri-state circuit produces the usual 0 and 1 voltages, but also
has a third high impedance Z (or Hi-Z)
▫ Useful for isolating circuits from common bus lines
▫ In Hi-Z case, the output capacitance can hold a voltage
even though no hardwire connection exists
(a) Symbol and operation (b) Tristate Inverter (c) Tri-state layout

10. Tri-state Logic
• A non-inverting circuit (a buffer) can be obtained by adding a
regular static inverter to the input
(a) EN = 0, f = Z
Output isolated from both
power supply and ground
(a) EN = 1, f = Data
Normal operation

11. Dynamic Logic Circuits
• A dynamic logic gate uses clocking and charge
storage properties of MOSFETs to implement
logic operations
▫ Provide a synchronized data flow
▫ Result is valid only for a short period of time
▫ Less transistors, and may be faster than static
cascades
• Based on the circuit in Figure 3
▫ The clock drives a complementary pair of
transistors Mn and Mp
▫ Precharge phase , pMOS is ON, Vout high
▫ Evaluation phase , pMOS is OFF1
0

Figure 3 Basic dynamic logic gateC

12. Dynamic Logic Circuits
Dynamic Inverter
Dynamic NOR

13. Dynamic Logic Circuits
• During evaluation, dynamic gates
require monotonically rising inputs
▫ Start LOW, remain LOW
▫ Start LOW, rise HIGH
▫ Start HIGH, remain HIGH
▫ Cannot start HIGH and fall LOW
Fig 4 Dynamic logic gate example

14. Dynamic Logic Circuits
• Monotonicity problems
• Dynamic gates produce monotonically falling outputs during
evaluation
• Illegal for one dynamic gate to drive another

15. Dynamic Logic- Charge sharing
• The origin of the charge sharing problem is the
parasitic node capacitance C1 and C2
▫ When clock , and the capacitor voltage V1
and V2 are both 0 V at this time, the total
charge is
▫ The worst-case charge sharing condition is
when the inputs are at (a, b, c) = (1, 1, 0)
▫ The principle of conservation of charge
1
Charge sharing circuit
DDoutVCQ 
fout VVVV  12 (When the current flow ceases)
fout
fffout
VCCC
VCVCVCQ
)( 21
21


DD
out
out
f V
CCC
C
V 







21
1
21






 CCC
C
out
out
DDf VV 
21 CCCout 
DDoutfout VCVCCCQ  )( 21

16. Domino Logic Circuits
• Follow dynamic stage with
inverting state gate
▫ Dynamic/static pair is called
Domino gate
▫ Produces monotonic outputs
▫ Non-inverting
▫ Useful in cascade operation

17. Domino Logic Circuits
Layout for domino
AND gate
Domino AND gate Domino OR gate