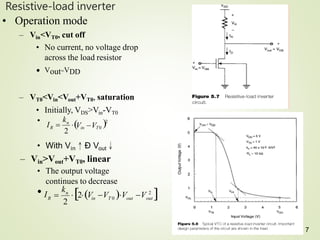
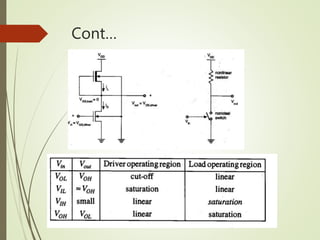
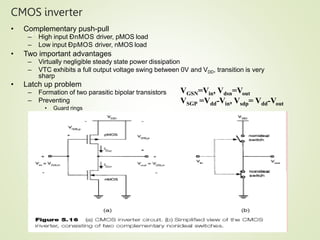
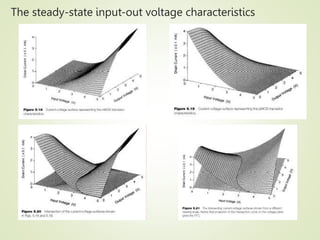
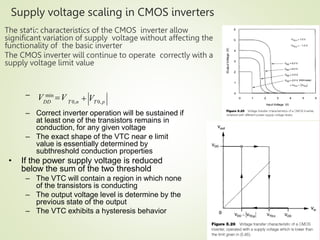
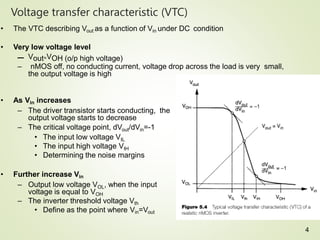
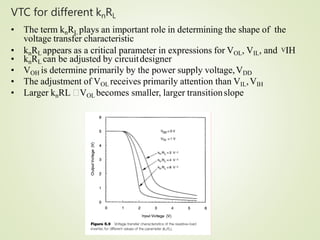
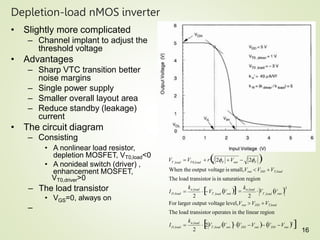
1. The document discusses the static characteristics of MOS inverters, including their voltage transfer characteristic (VTC). The VTC describes the output voltage (Vout) as a function of the input voltage (Vin) under DC conditions. 2. Key parameters that determine the VTC include the threshold voltage of the driver transistor (VT0), the product of kn and the load resistance (knRL), and the power supply voltage (VDD). Larger knRL results in a steeper transition slope and smaller output low voltage (VOL). 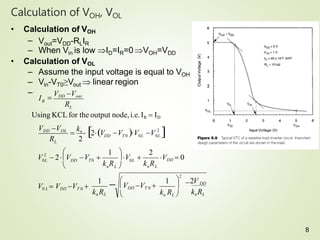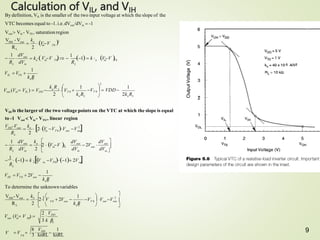3. Calculations are shown for determining the output high (VOH) and low (VOL) voltages, as well as the input voltages (VIL,

1. 1
Chapter 3
MOS Inverters:
Static Characteristics

2. MOS Inverter
• Positive logic convention
– “1” represents high voltage of VDD
– “0” represents low voltage of 0
• The inverter threshold voltage, Vth
– The input voltage,
0<Vin<Vth Doutput VDD
– The input voltage,
Vth<Vin<VDD Doutput 0
2

3. General circuit structure of an nMOS inverter
• The driver transistor
– The input voltage V
IN
=V
GS
– The output voltage
V
out
=V
DS
– The source and the
substrate are ground, VSB=0
• The load device
– Terminal current IL, terminal
voltage VL
ID(Vin,Vout)=IL(VL)
3

4. Voltage transfer characteristic (VTC)
• The VTC describing Vout as a function of Vin under DC condition
• Very low voltage level
– Vout=VOH (o/p high voltage)
– nMOS off, no conducting current, voltage drop across the load is very small,
the output voltage is high
• As Vin increases
– The driver transistor starts conducting, the
output voltage starts to decrease
– The critical voltage point, dVout/dVin=-1
• The input low voltage VIL
• The input high voltage VIH
• Determining the noise margins
• Further increase Vin
– Output low voltage VOL, when the input
voltage is equal to VOH
– The inverter threshold voltage Vth
• Define as the point where Vin=Vout
4

5. Noise immunity and noise margin
• NML=VIL-VOL
• NMH=VOH-VIH
• The transition region, uncertain
region
5
• VIL is the maximum
allowable voltage
Vin<VOL LOGIC 0
Vin>VIL as a result of noise
• VIH is the minimum
allowable voltage
Vin>VOH LOGIC 1
Vin<VIH as a result of noise

6. 6
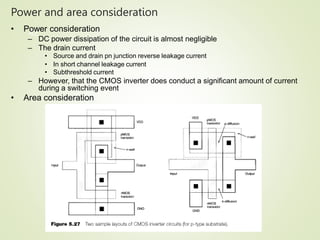
Power and area consideration
• The DC power dissipation
– The product of its power supply voltage and the amount of current
down from the power supply during steady state or in standby mode
– PDC=VDDIDC=(VDD/2)[IDC(Vin=low)+IDC(Vin=high)]
– In deep submicron technologies
• Subthreshold current more power consumption
• The chip area
– To reduce the area of the MOS transistor
• The gate area of the MOS transistor
• The product of W and L

7. Resistive-load inverter
• Operation mode
– Vin<VT0, cut off
• No current, no voltage drop
across the load resistor
• Vout=VDD
– VT0<Vin<Vout+VT0, saturation
• Initially, VDS>Vin-VT0
•
• With Vin↑Ð Vout↓
– Vin>Vout+VT0, linear
• The output voltage
continues to decrease
2
2
in T0
n
R
k
V V
I  
2
out
in T 0 out
n
R
• I
k
2V V V V 2


7

8. Calculation of VOH, VOL
• Calculation of VOH
– Vout=VDD-RLIR
– When Vin is low ID=IR=0 VOH=VDD
• Calculation of VOL
– Assume the input voltage is equal to VOH
– Vin-VT0≥Vout  linear region
–
kn RL
V0 L  VDD VT 0 
n L
DD T0
L
L
R
2V
k R
VDD  0
k R
0L
V 
R
VDD VOL
R
I 
VDD Vout
1  DD
knRL
1
2
1
2
Using KCLfor the output node,i.e.IR  ID
2
0L
2
0L
DD T 0 0L
V V

kn
 2V V 

kn RL 

2

 VDD VT 0 


n L 




V  2 V V 
8

9. 9
Calculation of VIL, and VIH
VIH is the larger of the two voltage points on the VTC at which the slope is equal
to -1 Vout  Vin - VTO , linear region
n L
out in IH
n L
n L
IH T 0 out
out
L
out
out
in
out
out n
L in
L
2knRL
2 kn RL
n L
IL T0
L
out
L in
V  V 
3 k R
2

VDD
V (V  V ) 
k R
k R
V  V  2V 
R
dV
dV
 2V 
dV
dV
R dV 2
1 dV k
n in T0
in T0
V  1 2V 

1
 1  k V
R 2
k R
V  V 
R
n in T0
n in T0
V V  
1
 1  k  VV 
 k 
R dV
1 dV
R 2
T 0 out
To determine the unknownvariables
1
1
1
1
2
R
V - V k
2
in T0

2
L
VDD -Vout
2
in T 0 out out
VDD-Vout

kn
 2 V V V V 

2
L
DD out n

8

VDD 1
 



VT 0
 Vout Vout 

kn
  1
 2V 
  2V

in 




V V 
  2  
 

k R 
VT 0   VDD

Vout (Vin  VIL )  VDD  n L
VT 0 
 
  VV
By definition, VIL is the smaller of the two input voltage at which the slope of the
VTC becomes equal to -1.i.e.dVout/dVin  -1
Vout  Vin - VT0 , saturationregion
T 0 3 knRL knRL

10. VTC for different knRL
10
• The term knRL plays an important role in determining the shape of the
voltage transfer characteristic
• knRL appears as a critical parameter in expressions for VOL, VIL, and VIH
• knRL can be adjusted by circuitdesigner
• VOH is determine primarily by the power supply voltage,VDD
• The adjustment of VOL receives primarily attention than VIL,VIH
• Larger knRL VOL becomes smaller, larger transitionslope

11. L
11
Power consumption
• The average power consumption
– When input low, VOL
• The driver cut-off, no steady-state current flow, DC power
consumption is zero
– When input high, VOH
• Both driver MOSFET and the load resistor conduct a
nonzero current
• The output voltage VOL, so the current ID=IR=(VDD- VOL)/RL
– P 
VDD

VDD VOL
2 R
DC(average)

12. Problem-1

15. Problem-2

18. Chip area
18
• The chip area depend on two
parameters
– The W/L ratio of the driver
transistor
• Gate area WxL
– The value of the resistor RL
• Diffused resistor
– Sheet resistance 20 to
100Ω/square
– Very large length-to-width rations
to achieve resistor values on the
order if tens to hundreds of kΩ
• Ploysilicon resistor
– Doped polysilicon (for gate of the
transistor), 20 to 40 Ω/square
– Undoped polysilicon, Rs Rs~10M
Ω/square
– The resistance value can not be
controlled very accurately Ð large
variation of the VTC
– Low power static random access
memory (SRAM)

19. Inverters with n-type MOSFET load
19
• The resistive-load inverter
– The large area occupied by the load resistor
• The main advantage of using a MOSFET as
the load device
– Smaller silicon area occupied by the transistor
– Better overall performance
• Enhancement-load nMOS inverter
– The saturated enhancement-load inverter
• A single voltage supply
• A relative simple fabrication process
• VOH=VDD-VT,load
– The linear enhancement-type load
• VOH=VDD
• Higher noise margins
• Two separate power supply voltage (drawback)
– Both type suffer from relatively high stand-by
(DC) power dissipation
• Not used in any large-scale digital applications

20. 16
Depletion-load nMOS inverter
• Slightly more complicated
– Channel implant to adjust the
threshold voltage
• Advantages
– Sharp VTC transition better
noise margins
– Single power supply
– Smaller overall layout area
– Reduce standby (leakage)
current
• The circuit diagram
– Consisting
• A nonlinear load resistor,
depletion MOSFET, VT0,load<0
• A nonideal switch (driver) ,
enhancement MOSFET,
VT0,driver>0
– The load transistor
GS
• V =0, always on
–
2
D,load
D,load
2
The load transistor operates in the linear region
2 2
T ,load out
T ,load out
n,load
out
DD
T ,load out DD out
n,load
F out F
T ,load T 0,load
V
k

2V V V V  V V 2

I 
k
For larger output voltage level,Vout VDD VT,load
2

kn,load
 V
V V
When the output voltage is small,Vout  VDD VT,load
The load transistor is in saturation region
V V  r 
2 V  2
I 

21. Cont…

22. 17
Calculation of VOH, VOL, VIL, ViH
When Vin is smaller thanVT0  driver  off, load  linear region
zero drain current,VOH VDD
2
2
VOH  VT ,load VOL 
VT 0 
2
n,load
D,load
2
2
T ,load OL
2
VOL  VOH
load
OL
OL
T0
OH
driver
OH DD OH
DD
T ,load OH
To calculate the output low VOL
assume,Vin  VOH  VDD  driver  linear region, load  saturation region
2V V V V V
 V 2
 0
k
k
 V
k
I 

 driver 
 kload

k
VT 0

2V V V V
   V 2

23. 18
Calculation of VOH, VOL, VIL, VIH
out DD T ,load out

V V  V V 
 kload 
VIL  VT 0 
DD out
out
driver in T0
k  VV 
DD out DD out
load
driver
dV
dV
dV
k
k k
T ,load out
T ,load out
2
in T0
load
2
2 2
sbustitute dVout /dVin  -1







Differential both sides with respect toVin

out 
 dV 
T ,load

 2V V




dVT ,load 



  2VDD Vout 
out 
dVT ,load 

2V V 


2V V V V V
 V 2

 VV  
Calculation of VIL
The driver  saturation region, the load  linear region
Vout
2 2F
dVout
dVT,load


load
dV
k
k
V 
V V
Differentialboth sides with respect toVin
kdriver
2V

 out 
V 
V
 driver 
 kload 
V V  2V 
 dVT ,load 
T ,load out
IH T 0 out
 
 dVout   dVin 
 k V V 



 dVin 
 Vout  
 dVin 
 dVout   dVout 
sbustitute dVout /dVin -1
 dVT ,load   dVout 
T ,load out
kdriver Vout  Vin VT 0 
2 2
 kdriver 
Calculation of VIH
The driver  linear region, the load  saturation region
V V 2
T ,load out
2 load
in T 0 out out

24. VTC of depletion load inverters
24
• The general shape of the
inverter VTC, and ultimately,
the noise margins, are
determined by
– The threshold voltage of the
driver and the load
• Set by the fabrication process
– The driver-to-load ratio
kR=(kdriver/kload)
• Determined by the (W/L)
ratios of the driver and the
load transistor
• One important observation
– A sharp VTC transition and
larger noise margins can be
obtained with relative small
driver-to-load ratios
• Much small area occupation

25. Design of depletion-load inverters
25
• The designable parameters in the inverter circuit are
– The power supply voltage VDD
• Being determined by other external constrains
• Determining the output level high VOH=VDD
– The threshold voltages of the driver and the load
• Being determined by the fabrication process
– The (W/L) ratios of the driver and the load transistor
•
• Since the channel doping densities are not equal
– The channel electron mobilities are not equal
– K’n,load≠k’n,driver
• The actual sizes of the driver and the load transistor are
usually determined by other constrains
– The current-drive capability
– The steady state power dissipation
– The transient switching speed
R
R
load
V V
R
L
 W
driver
,k 
k
k
 driver

2V V V V 2
OH T 0 OL OL
2
T ,load OL
k  
   
 L load  Lload
 W
  
L


W   W
driver
,k
kn,load 
kn,driver 

26. Power consideration
• The steady-state DC power consumption
– Input voltage low
• The driver off, Vout=VOH=VDD
• No DC power dissipation
– Input voltage high, VinVDD and Vout=VOL
•
V V 2
T ,load OL
26
T ,load OL
V V 2

VDD

kload
2 2
Assume the input voltage levellow 50% operation
time and high during the other 50%
2
2
OH T 0 OL OL
DC
driver
P
K
2V V V V 2


Kload
IDC Vin  VDD


27. Area consideration
27
• Figure (a)
– Sharing a common n+
diffusion region
• Saving silicon area
– Depletion mode
• Threshold voltage adjusted by
a donor implant into the
channel
– (W/L)driver>(W/L)load, ratio
about 4
• Figure (b)
– Buried contact
• Reducing area
• For connecting the gate and
the source of the load
transistor
– The polysilicon gate of the
depletion mode transistor
makes a direct ohmic with
the n+ source diffusion
– The contact window on the
intermediate diffusion area
can be omitted

28. Example 5.3 (1)

29. Example 5.3 (2)

30. Example 5.3 (3)
30

31. CMOS inverter
31
• Complementary push-pull
– High input ÐnMOS driver, pMOS load
– Low input ÐpMOS driver, nMOS load
• Two important advantages
– Virtually negligible steady state power dissipation
– VTC exhibits a full output voltage swing between 0V and VDD, transition is very
sharp
• Latch up problem
– Formation of two parasitic bipolar transistors
– Preventing
• Guard rings
VGSN=Vin, Vdsn=Vout
VSGP =Vdd-Vin, Vsdp= Vdd-Vout

32. Circuit operation
• Region A: Vin<VT0,n
– nMOS off, pMOS on Ð ID,n=ID,p=0,
Vout=VOH=VDD
• Region B: Vin>VT0,n
– nMOS saturation, the output
voltage decreases
– The critical voltage VIL, (dVout/dVin)=-1
is located within this region
– As the output further decreases
ÐpMOS enter saturation, boundary
of region C
• Region C:
– If nMOS saturation Ð VDS,nVGS,n-
VT0,n  Vout Vin-VT0,n
– If pMOS saturation Ð VDS,nVGS,p-
VT0,p  Vout Vin-VT0,p
– Both of these conditions for device
saturation are illustrated graphically as
shaded areas
• Region D: Vout<Vin-VT0,p
– The criical point VIH
• Region E: Vin>VDD+VT0,p
– Vout=VOL=0

33. Circuit operation
33
• The nMOS and the pMOS transistors an be
seen as nearly ideal switches
– The current drawn from the power supply in both
these steady state points region A and region E
• Nearly equal to zero
• The only current Ðreverse biased S, D leakage current
– The CMOS inverter can drive any load
• Interconnect capacitance
• Fan-out logic gates
• Either by supplying current to the load, or by sinking current
from the load

34. The steady-state input-out voltage characteristics
34

35. 30
Calculation of VIL, VIH
k V V  k 2V V V V 
p

kn
R
R
IL
substituting Vin  VIL and (dVout /dVin )  -1
n IL T 0.n p out IL T 0, p DD
p
out DD
n
n
k
1 k

2Vout  VT 0, p VDD  kRVT 0,n
wherek
V
k
V V V
k
V V 
2 p
GS ,n T0,n
k




 dVin 
 dVout 
  Vout VDD  Vout VDD 
 dVin 
 dVout 
V V V 
k V V  k   in DD T 0, p
n in T0,n
2
2
2
V  V V 2

in DD T 0, p out DD

V V 2

kp

2
V
in T0,n
2V V V V 2

GS , p T 0, p DS,P DS,p
2
nMOSsaturation, pMOSlinear
V V
kn
 2V 
V V V 2
V V V 
 k  
n
V V  k 2V V 
k V V  2V  k 
V V V 
substitingVin VIH and(dVout /dVin )  -1
out T0,n
DD T 0,p R
out p IH DD T0,p
IH T0,n
in DD T0,p
out
V 
k
V 
V
V V



  dVout 
 dVin   dVin 
 dVout 
V V   V V  
out out
k   p in DD T0,p
n in T0,n
2
2
in T 0,n out
2 2
2 p
2
GS, p T0,p
kn
 2V V 2

kp
V
GS,n T 0,n DS,n DS,n
nMOSlinear, pMOSsaturation

36. 2
th T 0,n th T 0,p
36
value between V -V and 
V -V 
If Vin  Vth , the output vol tage can actually attain any
th
DD T 0,p

V V 
n
n
DD
2
T 0,p
in
T 0,n
in
T 0,p
GS ,p
GS ,n T 0,n
k
DD T 0,p
T 0,n
V
k
kp
k
T 0,n
V V
 1 
1  
 k R 
V 
1
V V 
R
2
V 2

k p

V
2
kn
V
2
2
kn
V V 2

k p

V V
Calculation of Vth
The inveter th reshold voltage is defined as Vth  Vin  Vout
Since the CMOS inverter exhibits large noise margins and very sharp VTC transitio n the
inverter t hreshold voltage emerges as an imporant parameter characteri zing the DC
performanc e of the inverter
For Vin  Vout , both trans istor are in saturation mode

  V 

k p




Vin 1

37. Threshold voltage
37
• The Region C of VTC
– Completely vertical
• If the channel length modulation effect is neglected, i.e. if =0
– Exhibits a finite slope
• If >0
• Fig 5.22 shows the variation of the inversion (switching) threshold
voltage Vth as function of the transconductance ratio kR

38. VTC and power supply current
38
• If input voltage is either
smaller than VT0,n, or
larger than VDD+VT0,p
– Does not draw any
significant current from the
power supply
– Except for small leakage
current and subthreshold
currents
• During low-to-high and
high-to-low transitions
– Regions B, C, and D
– The current being drawn
from the power source
– Reaching its peak value
when Vin=Vth (both
saturation mode)

39. 34
Design of CMOS inverters
IL DD
VIL  VIH  VDD , NML  VIL VOL  VIL , NM H  VOH VIH  VDD VIH NM
L  NMH  VIL
 2V 
For a symmetric CMOSinverter withVT0,n  VT0,p and kR 1
n
p
n
n
assumetox, Cox have the same value for nMOS and pMOS
p
n
n
p OX
n
n
n
kp
inverter
n
we can achievecomplelysymmetric input -output characteristics by settingVT0 VT 0,n  VT0,p
DD
R
 L
L

L


L

k
k

symmertric
p 
 k
k
k
 
 L
 
 
 L  p

L

  p
 W
   2.5
230cm2
/V s W   W
W   580cm2
/V  s
 

 
 p  p
OX 
L

 
 W
W    W 
  W 
 C
 C

1

 
  


 
p ideal
 k 

 0.5V V
 k   0.5 V
substituting 5.74 in 5.73   n 

2
DD T 0,n 
VDD T 0, p 


 
V V
V V
 n
 
k V V V
V V V
8 8
V 
1
3V  2V ,V 
1
5V
T 0,n IH DD T0,n
2

1
V s
The switching threshold voltageof an idealinverter is defined as Vth,ideal
1 
2
th T0,n
DD T 0, p th 
R DD T 0,p th p
th T 0,n
 k


40. Example 5.4
40

41. Supply voltage scaling in CMOS inverters
The static characteristics of the CMOS inverter allow
significant variation of supply voltage without affecting the
functionality of the basic inverter
The CMOS inverter will continue to operate correctly with a
supply voltage limit value
41
– Correct inverter operation will be sustained if
at least one of the transistors remains in
conduction, for any given voltage
– The exact shape of the VTC near e limit
value is essentially determined by
subthreshold conduction properties
• If the power supply voltage is reduced
below the sum of the two threshold
– The VTC will contain a region in which none
of the transistors is conducting
– The output voltage level is determine by the
previous state of the output
– The VTC exhibits a hysteresis behavior
DD T 0,n T 0, p
 V
– V min
V

42. Power and area consideration
42
• Power consideration
– DC power dissipation of the circuit is almost negligible
– The drain current
• Source and drain pn junction reverse leakage current
• In short channel leakage current
• Subthreshold current
– However, that the CMOS inverter does conduct a significant amount of current
during a switching event
• Area consideration

43. Basic CMOS NOR and NAND Gates
(a) Two-input CMOS NOR logic circuit and (b)
truth table

44. Cont….
(a) Two-input CMOS NAND logic circuit
and (b) truth table

45. Problem
 Design 2 input CMOS NOR gate and NAND gate
circuits to give following parameters.
 NML = 1.65 V, NMH = 2.4V,
 VDD = 5 V,
 VT0,n = |VT0,p| = 0.7 V
 µnCOX = 40 µA/V2
 µpCOX = 20 µA/V2