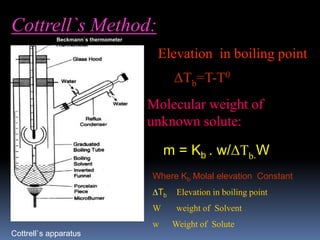
The document provides an overview of colligative properties of dilute solutions, including boiling point elevation and freezing point depression, and describes methods for determining the molecular weight of solutes using these properties. It discusses equations for calculating changes in boiling and freezing points, examples, and numerical problems related to the topic. Additionally, it mentions the Van 't Hoff factor and references for further reading on physical chemistry.

1. Mr. Nitin H. Bansod
Shri shivaji Science College,
Amravati.

2. Contents :
Defination of Solution
 Colligative Properties
Elevation in boiling point
 Cottrell’s Method
Applications
References

3. Solution :
Colligative properties are shown by
dilute solutions containing non-volatile &
non-electrolyte solute.
These properties are the properties of
dilute solution that's why these are term as
colligative properties of dilute solution.
The molecular weight of the non-volatile
solute can be determined with the help of
colligative property

4. Colligative Properties:
Colligative properties depend only on the
number of solute particles present, not on
the nature of the solute particles.

7. Boiling-Point Elevation:
DTb = Tb – T b
0
Tb > T b
0
DTb > 0
T b is the boiling point of
the pure solvent
0
T b is the boiling point of
the solution
DTb = Kb m
m is the molality of the solution
Kb is the molal elevation
constant or ebullioscopic
constant(0C/m)
V
a
p
o
u
r
p
r
e
s
s
u
r
A
B
C

8. Beckmann`s thermometer
Cottrell`s apparatus
ΔTb=T-T0
Elevation in boiling point
Molecular weight of
unknown solute:
Cottrell`s Method:
m = Kb . w/ΔTb.W
Where Kb Molal elevation Constant
∆Tb Elevation in boiling point
W weight of Solvent
w Weight of Solute

9. Depression in the freezing point of solution or
Cryoscopy:(Greek cryo = cold, scopos = observe "observe the
cold") and relies on exact measurement of the freezing point.
The temp. at which solid and liquid phases of substance have
same vapour pressure is called as freezing point of liquid.
When non volatile solute is dissolved in a volatile solvent the
freezing point of the solution decreases due to decrease in vapour
pressure of solution. This decrease in the freezing point of solvent
due to addition of solute is called depression in freezing point of
solution. ΔTf = T0 -T

10. Thermodynamic derivation of relation between depression of freezing point and
molecular weight of solute :

11. Numerical Problems: (Important)
1. An aqueous solution containing 2.5 ×10-4 kg of solute dissolved in 2×10-2 kg of
water froze at 272.58 k. calculate the molar mass of the solute.
(Kf = 1.85 k kg mol-1 ) Summer -2013 -03 marks
Solution : We have the formula
Here ΔTf = To - T = 273 -272.58 = 0.42
m = Kf. w/ΔTf.W
= 1.85 × 2.5 ×10-4
0.42 × 2×10-2
= 55.08×10-03 kg mol-1

12. 2. A solution containing 10-2 kg of sodium chloride in 1 kg of water freezes at 272.396
k. the Kf for water is 1.85 K kg mole-1 calculate the molar mass of the solute.
Solution :
m = Kf. w/ΔTf.W
= 1.85 × 10-2
0.604 × 1
= 30.629× 10-3 kg mol-1

13. 3. Calculate he Molal depression constant (Kf)of water . The heat of fusion of ice at 273
K is 6024.6 J mol-1 . ( R= 8.314 J K-1 mol-1 and M= 18×10-3 kg)
Solution Kf = MRTo2 / Lf
= 18 × 10-3 × 8.314 × (273)2 / 6024.6
= 1.851 K Kg Mole-1

14. 4. An aqueous solution containing 2.5 × 10-4 kg of solute dissolved in 2 × 10-2 kg of
water froze at 272.58 K. Calculate the molar mass of solute. Heat of Fusion of ice
at 273 K is 6024.6 J mol-1
Solution : first calculate the molal depression constant (Kf ) of Water
Kf = MRTo2 / Lf
= 18 × 10-3 × 8.314 × (273)2 / 6024.6
= 1.851 K Kg Mole-1
Here ΔTf = To - T = 273 -272.58 = 0.42
m = Kf. w/ΔTf.W
= 1.85 × 2.5 ×10-4
0.42 × 2×10-2
= 55.08 ×10-3 kg mol-1

15. 5. A solution containing 3 10-4 kg of benzoic acid in 2 × 10-2 kg of
benzene freezes at 0.317 K below the freezing point of solvent .
Calculate the Molar mass of solute?
Solution :

16. Rast’s Method :
liquid f.p Solid
m.p
There are 9 unknowns. Their names and molar masses are:
Naphthalene (128.2) Anthracene (178.2) Cholanthrene (254.3)
Dichlorobenzene (147.0) Anthrone (194.2) Cholane (330.6)
Naphtoquinone (158.2) Benzil (210.2) Cholestane (372.7)
Introduction: When one mole of a solute is contained in 1 kg of solvent, the melting point of that
mixture is lowered by a characteristic amount. That amount is called the molal freezing point
depression constant, or Cryoscopy Constant (Kf.)
m = Kf. w/ΔTf.W
Kf = Molecular depression constant for camphor (39.7)
w = Weight (mass) of unknown compound (solute)
W = Weight (mass) of camphor (solvent)
ΔTf = Depression of melting point
M = gram molecular weight of solute
In this simulation you will be asked to find the molecular weight of an unknown solid by
measuring the depression of the melting point of camphor when the solid is mixed with it.

17. Colligative properties for nonvolatile solutes:
Take it to the bank
•Vapour pressure is always lower
•Boiling point is always higher
•Freezing point is always lower
•Osmotic pressure drives solvent from lower concentration to
higher concentration

18. Abnormal Mass and Vant Hoff Factor (i ) :
i) The solution is dilute and behaves ideally
ii) High Concentration and non ideality of Solution
iii) The solute molecule may associate or dissociate in the solution
Vant Hoff introduced factor “ i” called Vant Hoff factor to measure the deviation in
observed value of colligative property from its normal value
I = Observed Colligative Property
Normal Colligative Property

20. References:
A Textbook of Physical Chemistry : Gurdeep Raj
Physical chemistry : Puri Sharma and Pathania
A Textbook of Physical Chemistry : Kapoor
A Textbook of Physical Chemistry : Bokey prakashan
www.khan academy

21. Thank You