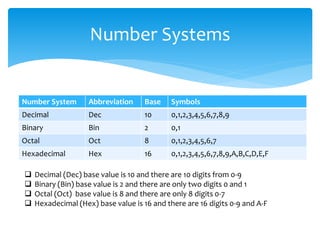
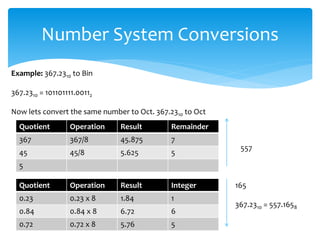
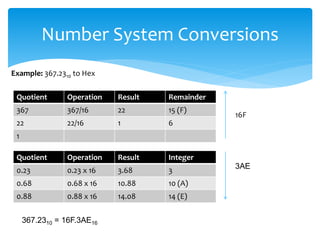
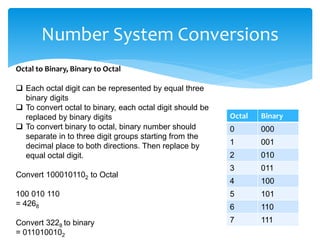
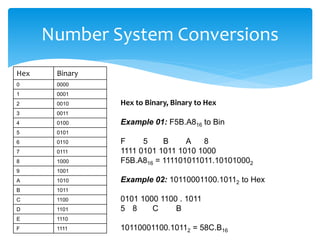
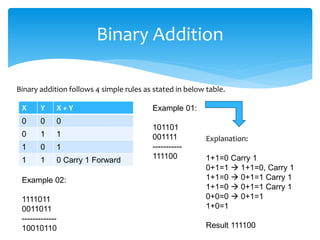
This document provides an overview of data representation in computers, focusing on number systems such as decimal, binary, octal, and hexadecimal. It explains the fundamental concepts of these number systems, including their bases and how to convert between them. The document highlights the importance of mastering these concepts for understanding computer technology and preparing for exams.

1. Computer and Network
Technology (CNT)
Chapter: Fundamentals
Lesson: Data Representation in Computers
Number systems and conversions
Lecture 01 bcsonlinelectures.com

2. Data Representation in Computers
 In this section we are going to learn about how things stored in a computer.
As we know computer can store things we call “Data” in storage devices such
as hard drives and in memory.
 As we know a computer can store so many different type of data such as
images, videos, text documents, data bases, etc. But there is one fundamental
thing we should understand is that a computer can understand on zeros and
ones (0 and 1).
 So we need to understand how a computer store these all types of data using
only 1 and 0. To understand this we need to study about number systems.
 Here we are going to learn about decimal, binary, octal and hexadecimal
number systems.

3. Number Systems
 A number system is a way of representing numerical values. It’s a standard and
the most common number system is decimal and we all are using the decimal
number system for our day to day works. Other number systems are Binary,
Octal and Hexadecimal.
 A number system has a BASE (also called RADIX) and there are symbols to
represent a digit. The number of digits in a number system is equal to the value
(size) of the base.
 Our human mind is trained to use decimal number system. Computer uses binary
number system. We use octal and hexadecimal number systems to represent
small values or large and complex numerical values such as a very large amount.

4. Number Systems
Number System Abbreviation Base Symbols
Decimal Dec 10 0,1,2,3,4,5,6,7,8,9
Binary Bin 2 0,1
Octal Oct 8 0,1,2,3,4,5,6,7
Hexadecimal Hex 16 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
 Decimal (Dec) base value is 10 and there are 10 digits from 0-9
 Binary (Bin) base value is 2 and there are only two digits 0 and 1
 Octal (Oct) base value is 8 and there are only 8 digits 0-7
 Hexadecimal (Hex) base value is 16 and there are 16 digits 0-9 and A-F

5. Decimal Number System
 This is the number system we use in our day to day life and the most commonly used
number system.
 There are 10 digits in this number system (0 -9) and the base or radix of the system is
10
 There are negative numbers as well as positive numbers
 The root value of the base starts from 0 and count from right to left
Example
10n ….. 102, 101, 100
Let’s consider this number 1345. The last digit 5 is 100, 4 is 101, 3 is 102, 1 is 103. When we
multiply the number from Radix we get 1345.
1x103 + 3x102 + 4x101 + 5x100
Always remember base value 100 = 1, 101 = 10, 102 = 100 and so on…
So when we multiply base value with the digit and add all we get the number.
1000 + 300 + 40 + 5 = 1345
That is how base 10 number system is working.

6. Binary Number System
The binary number system has only two digits 0 and 1. The base of the binary number
system is 2. Like decimal number system, the value of the digit in a binary number is
depend on the position within the number. Let’s consider following binary number
and convert in to decimal to get it’s decimal value.
Example:
101101 is a binary number.
Now the base of these digits are 2. So, let’s multiply digit from its radix and decimal
value of it.
1x25 + 0x24 + 1x23 + 1x22 + 0x21 + 1x20 = 32 + 0 + 8 + 4 + 0 + 1
= 45

7. Octal Number System
Octal number system (short term Oct) has eight digits (0 – 7) and the base is 8. Since
Oct numbers can contain digits from zero to seven, number 98 is not an Oct number
and 478 is an Oct number because the base of the number is indicated as 8. Now
let’s get the decimal value of 478 we do the same method used above.
Example:
4x81 + 7x80 = 32 + 7
= 3910
According to the above example 478 in Oct equal to 3910 in Dec.
Oct number system mainly use in computing. We will discuss in a later chapter when
and where Oct system is used and some applications of it.

8. Hexadecimal Number System
Called Hex for short, this number system has 16 digits and mainly used to present
large numbers. This contains digits from 0 – 9 and A – F for additional numbers. E1016
is a hexadecimal number. We can get the decimal value of this number using the
same method we used previously.
The decimal value of English letters presented in Hex number system;
A = 10, B = 11, C =12, D = 13, E = 14, F = 15
Altogether (0 – F) there are 16 digits (including zero).
Example:
E1016 = 14x162 + 1x161 + 0x160
= 3584 + 16 + 0
= 360010

9. Number System Conversions
Decimal to Binary, Oct and Hex
 Decimal numbers may have an integer part and a fractional part. In number 454.67
integer part is 456 and fractional part is .67
 To convert decimal number in to any other number system, we need to take these
integer part and fractional part separately.
Converting integer part
 Divide the quotient repeatedly by the target base while recording remainders until
the quotient become zero or the quotient is less than the base value.
 Write the remainders from bottom to top order.

10. Number System Conversions
Example: 367.2310 to Bin
Quotient Operation Result Remainder
367 367/2 183 1
183 183/2 91 1
91 91/2 45 1
45 45/2 22 1
22 22/2 11 0
11 11/2 5 1
5 5/2 2 1
2 2/2 1 0
1 No longer be able to divide because
quotient is less than the base value
Convert
integer part:
101101111

11. Number System Conversions
Example: 367.2310 to Bin
Quotient Operation Result Integer
0.23 0.23 x 2 0.46 0
0.46 0.46 x 2 0.92 0
0.92 0.92x 2 1.84 1
0.84 0.84 x 2 1.68 1
Now this will create infinite fraction numbers.
Convert
fractional part:
0011
Convert fractional part
Repeatedly multiply the fractional part from the target base value while recording the
integer value while the fraction becomes zero or until the required number of
fractional positions met. Write the integer values from top to bottom.

12. Number System Conversions
Example: 367.2310 to Bin
367.2310 = 101101111.00112
Now lets convert the same number to Oct. 367.2310 to Oct
Quotient Operation Result Remainder
367 367/8 45.875 7
45 45/8 5.625 5
5
557
Quotient Operation Result Integer
0.23 0.23 x 8 1.84 1
0.84 0.84 x 8 6.72 6
0.72 0.72 x 8 5.76 5
165
367.2310 = 557.1658

13. Number System Conversions
Example: 367.2310 to Hex
Quotient Operation Result Remainder
367 367/16 22 15 (F)
22 22/16 1 6
1
16F
Quotient Operation Result Integer
0.23 0.23 x 16 3.68 3
0.68 0.68 x 16 10.88 10 (A)
0.88 0.88 x 16 14.08 14 (E)
3AE
367.2310 = 16F.3AE16

14. Number System Conversions
Bin, Oct, Hex to Decimal
To convert any Bin, Oct or Hex number to Dec is easy. All you have to do is multiply
base value of the position of the digit with digit value and get the sum of all values.
Lets convert 11101101.11012 to Decimal
1x27 +1x26+1x25+0x24+1x23+1x22+0x21+1x20.1x2-1+1x2-2+0x2-3+1x2-4
Note that 1x2-1 = 1 / 21 =0.5 and same method apply to others.
128+64+32+0+8+4+0+1 . 0.5+0.25+0+0.0625
= 237.812510

15. Number System Conversions
Bin, Oct, Hex to Decimal
Example:
Convert 547.28 to Decimal
5 4 7 . 2
82 81 80 . 8-1
5 x 64 + 4x8 + 7x1 + 2x0.125
= 320+32+7+0.250
= 359.25
547.28 = 359.2510

16. Number System Conversions
Octal to Binary, Binary to Octal
 Each octal digit can be represented by equal three
binary digits
 To convert octal to binary, each octal digit should be
replaced by binary digits
 To convert binary to octal, binary number should
separate in to three digit groups starting from the
decimal place to both directions. Then replace by
equal octal digit.
Convert 1000101102 to Octal
100 010 110
= 4268
Convert 3228 to binary
= 0110100102
Octal Binary
0 000
1 001
2 010
3 011
4 100
5 101
6 110
7 111

17. Number System Conversions
Hex to Binary, Binary to Hex
 Each hex digit can be represented by equal four
binary digits
 To convert hex to binary, each hex digit should be
replaced by binary digits
 To convert binary to hex , binary number should
separate in to four digit groups starting from the
decimal place to both directions. Then replace by
equal hex digit.
Hex Binary
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001
A 1010
B 1011
C 1100
D 1101
E 1110
F 1111

18. Number System Conversions
Hex to Binary, Binary to Hex
Example 01: F5B.A816 to Bin
F 5 B A 8
1111 0101 1011 1010 1000
F5B.A816 = 111101011011.101010002
Example 02: 10110001100.10112 to Hex
0101 1000 1100 . 1011
5 8 C B
10110001100.10112 = 58C.B16
Hex Binary
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001
A 1010
B 1011
C 1100
D 1101
E 1110
F 1111

19. Binary Addition
Binary addition follows 4 simple rules as stated in below table.
X Y X + Y
0 0 0
0 1 1
1 0 1
1 1 0 Carry 1 Forward
Example 01:
101101
001111
-----------
111100
Example 02:
1111011
0011011
-------------
10010110
Explanation:
1+1=0 Carry 1
0+1=1  1+1=0, Carry 1
1+1=0  0+1=1 Carry 1
1+1=0  0+1=1 Carry 1
0+0=0  0+1=1
1+0=1
Result 111100

20. Conclusions
 Number systems, conversion and addition are the basics of computer
technology. You need to have a good knowledge in this filed to understand
different operations in CPU and programing.
 This is also a very easy part to learn and takes little time and practice.
 There may be questions from number system conversions and binary addition
in the exam. These are the definite questions that you should answer and can
gain full marks.
 It takes very little time to answer questions from this area and you can save
time for more difficult problems in the exam.

21. End of Lecture 01
Computer and Network Technology
For more lecture notes http://bcsonlinelectures.com
Lecturer:
Susantha Herath
PGD in IT (BCS), PGD in Marketing (Uni. Of Kelaniya, Sri Lanka)