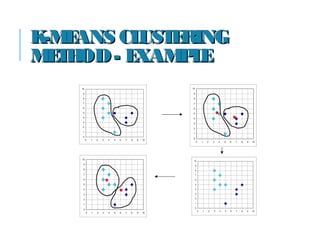
Cluster analysis is used to group objects that are similar to each other within the same cluster and dissimilar to objects in other clusters. It has various applications in marketing, land use, insurance, and city planning. There are different types of data that can be used for cluster analysis, including interval-scaled, binary, ordinal, and ratio variables. Major clustering methods include partitioning methods like k-means clustering and hierarchical clustering. K-means clustering partitions objects into k clusters by assigning objects to the cluster with the nearest centroid.

1. Cluster
analysis
Presented By:-
Shubham Goyal

2. •What is clusteranalysis?What is clusteranalysis?
•Types of data in clusteranalysisTypes of data in clusteranalysis
•Majorclustering methodsMajorclustering methods
•SummarySummary
ClusteranalysisClusteranalysis

3. Cluster:Cluster: a collection of data
objects
osimilar to one another within the
same cluster
odissimilar to the objects in the
other clusters
Aimof clustering:Aimof clustering: to group a set
of data objects into clusters
What is clusteranalysis?What is clusteranalysis?

4. APPLICATIONS OFCLUSTERINGAPPLICATIONS OFCLUSTERING
Marketing:Marketing: discovering of distinct customer
groups in a purchase database
Land use:Land use: identifying of areas of similar land use
in an earth observation database
Insurance:Insurance: identifying groups of motor insurance
policy holders with a high average claim cost
City-planning:City-planning: identifying groups of houses
according to their house type, value, and
geographical location

5. TYPEOFDATA IN CLUSTERTYPEOFDATA IN CLUSTER
ANALYSISANALYSIS
•Interval-scaled variablesInterval-scaled variables
•Binary variablesBinary variables
•OrdinalOrdinal
•RRatio variablesatio variables
•Complex data typesComplex data types

6. MAJORCLUSTERINGMAJORCLUSTERING
METHODSMETHODS
•Partitioning methods-
•K-means methodsK-means methods
•Hierarchical methodsHierarchical methods

7. K-MEANS CLUSTERINGK-MEANS CLUSTERING
METHODMETHOD
Input to the algorithmInput to the algorithm: the number of clusters k,
and a database of n objects
Algorithmconsists of fourstepsAlgorithmconsists of foursteps:
1. partition object into k nonempty subsets/clusters
2. compute a seed points as the centroidcentroid (the
mean of the objects in the cluster) for each
cluster in the current partition
3. assign each object to the cluster with the nearest
centroid
4. go back to Step 2, stop when there are no more
new assignments

8. K-MEANS CLUSTERINGK-MEANS CLUSTERING
METHOD- EXAMPLEMETHOD- EXAMPLE
0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6 7 8 9 10
0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6 7 8 9 10
0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6 7 8 9 10
0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6 7 8 9 10

9. Complexities of K-means
Time Complexity
Let tdist be the time to calculate the distance between two
objects
Each iteration time complexity:
O(Kn tdist)
K = number of clusters (centroids)
n = number of objects
Bound number of iterations I giving
O(I Kn tdist)
Space Complexity
For m-dimensional vectors

10. Strength of the k-Means
Clustering
• Relatively efficient: O (t k n), where n is number of
objects,
k is number of clusters, and t is number of iterations.
Normally k, t << n.
• K-Means may produce tighter clusters than
hierarchical
clustering.

11. Weakness of the k-means
Clustering
• Applicable only when mean is defined (works only for
numerical observations), then what about categorical
data?
• Need to specify k, the number of clusters, in advance.
• Unable to handle noisy data and outliers

12. •Clusteranalysis groups objectsClusteranalysis groups objects
based on theirsimilaritybased on theirsimilarity
•Clusteranalysis has wideClusteranalysis has wide
applicationsapplications
•Measure of similarity can beMeasure of similarity can be
computed forvarious type ofcomputed forvarious type of
datadata
•Selection of similarity measureSelection of similarity measure
is dependent on the data usedis dependent on the data used
and the type of similarity weand the type of similarity we
are searching forare searching for
SummarySummary

13. REFERENCES - CLUSTERINGREFERENCES - CLUSTERING
•R. Agrawal, J. Gehrke, D. Gunopulos, and P. Raghavan. Automatic subspace clustering of
high dimensional data for data mining applications. SIGMOD'98
• Ms.Avita Katal , Assistant professor ,Dept. of CS/IT , Graphic Era Hill University.