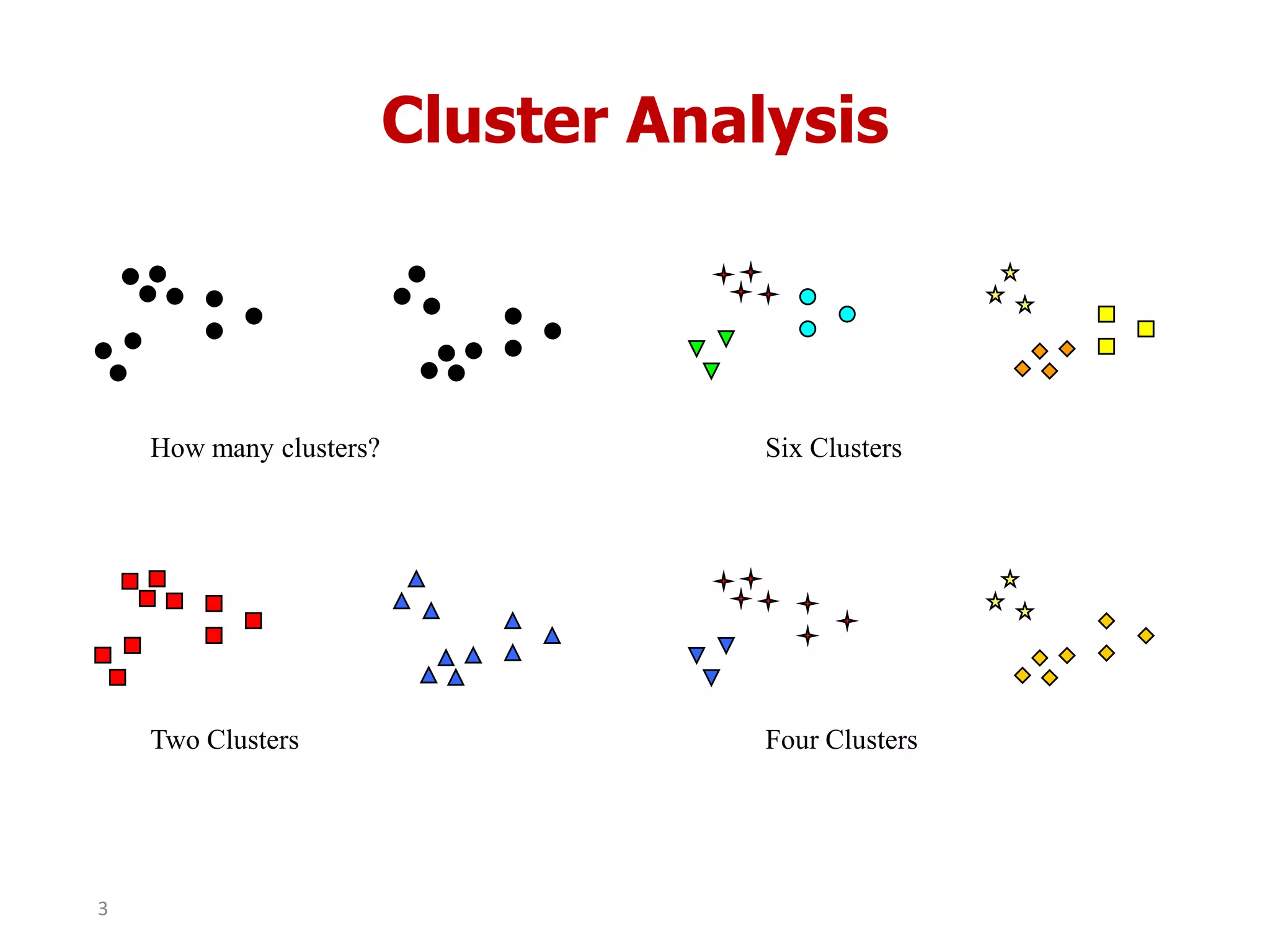
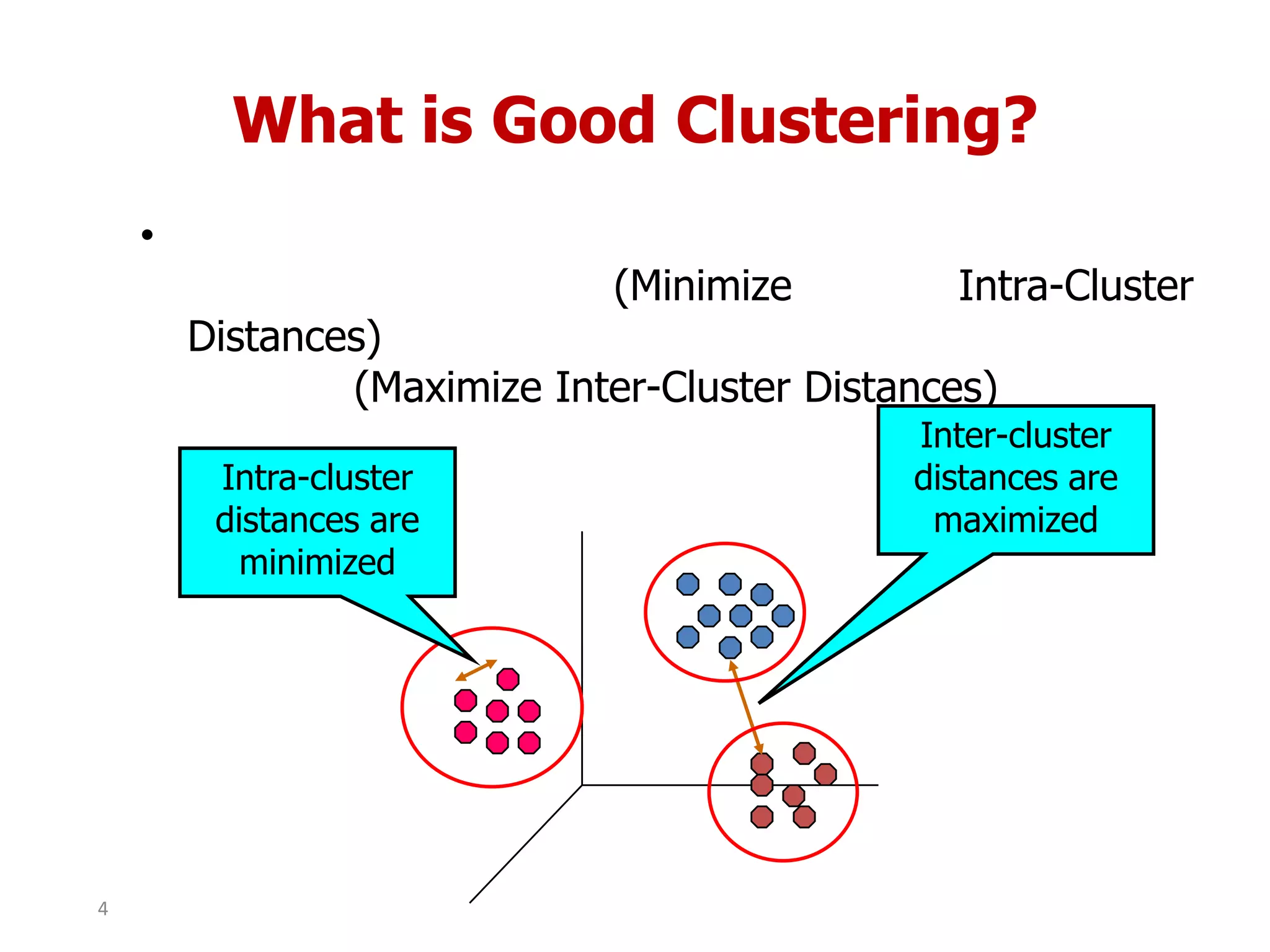
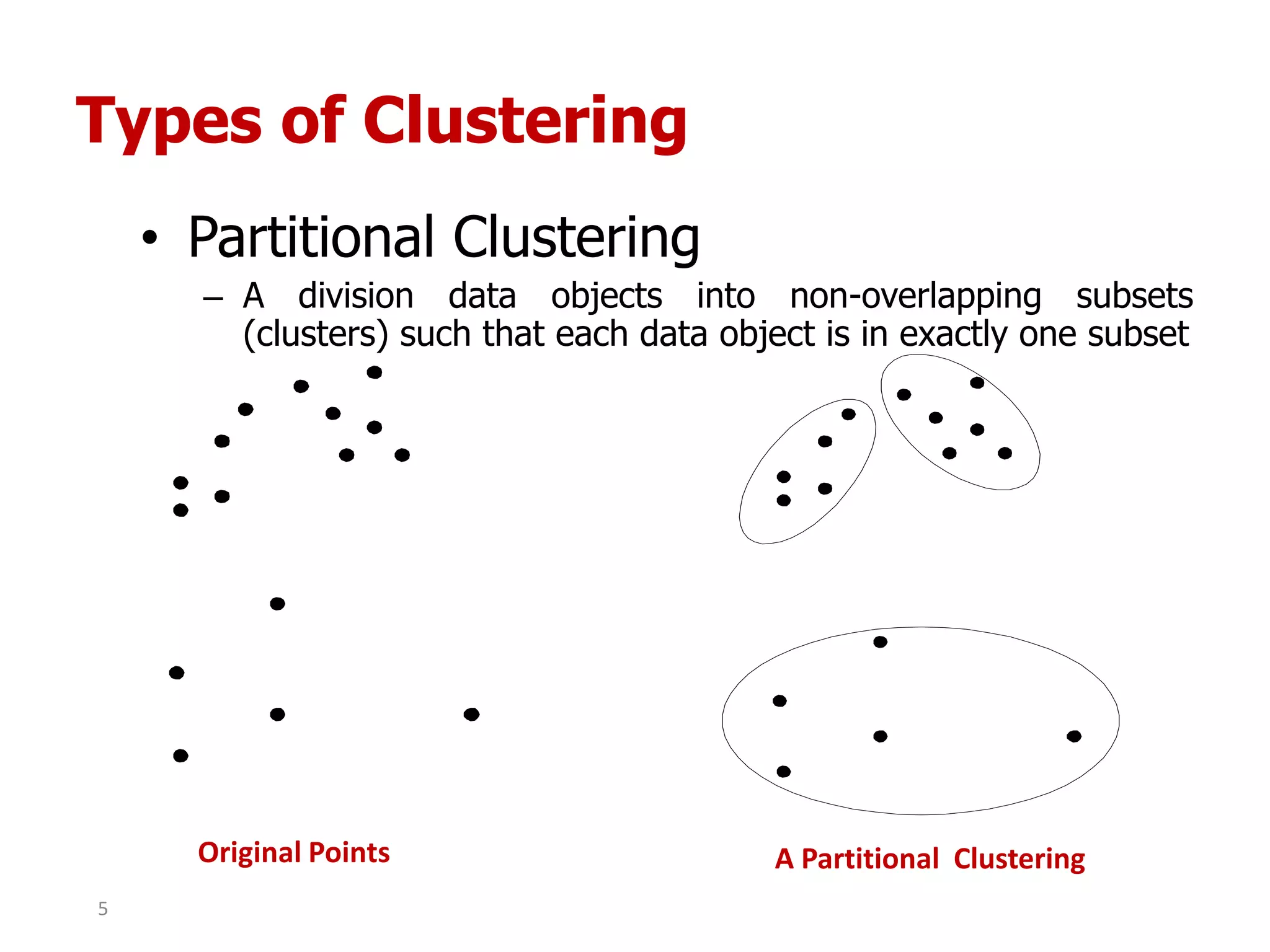
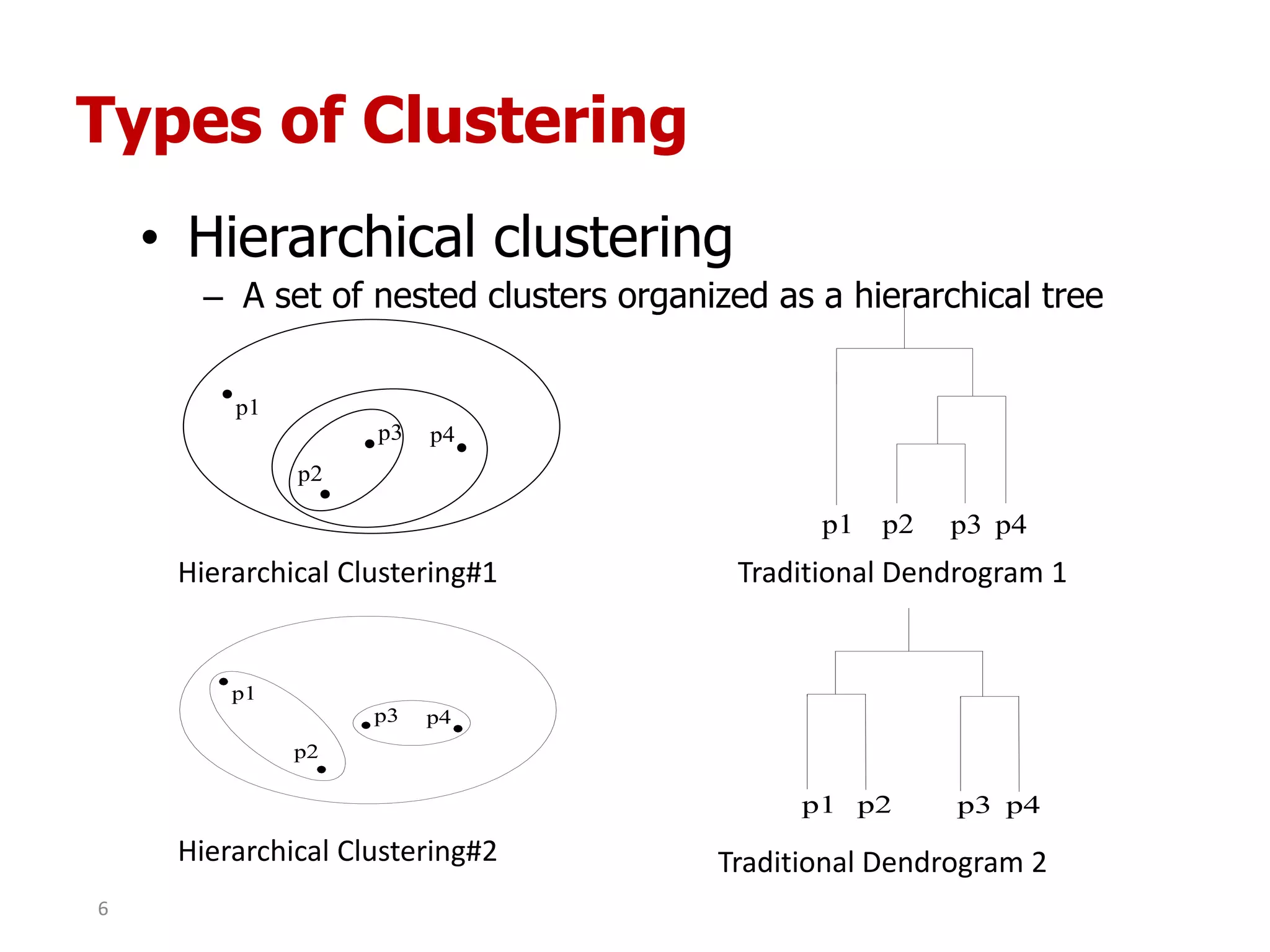
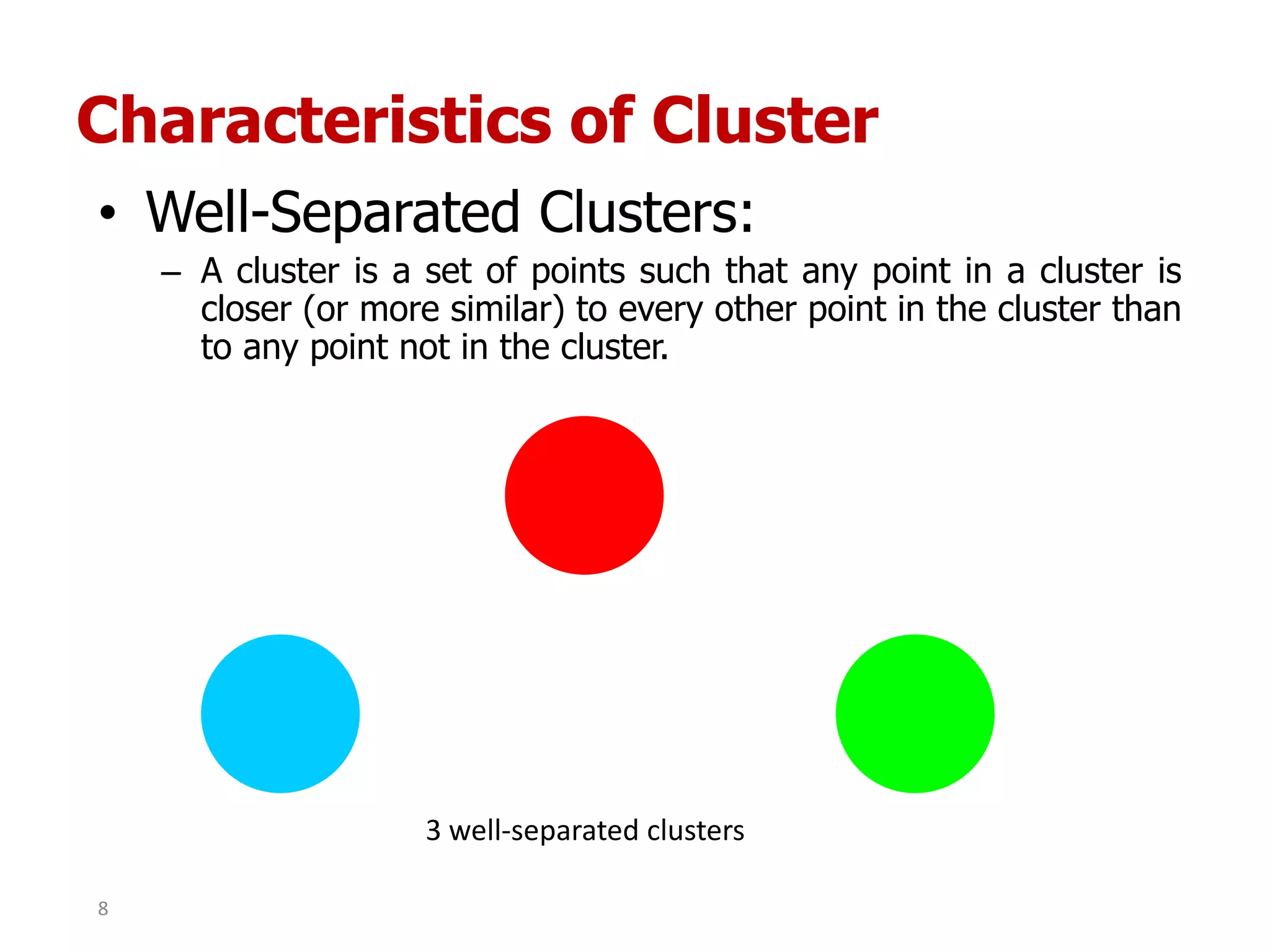
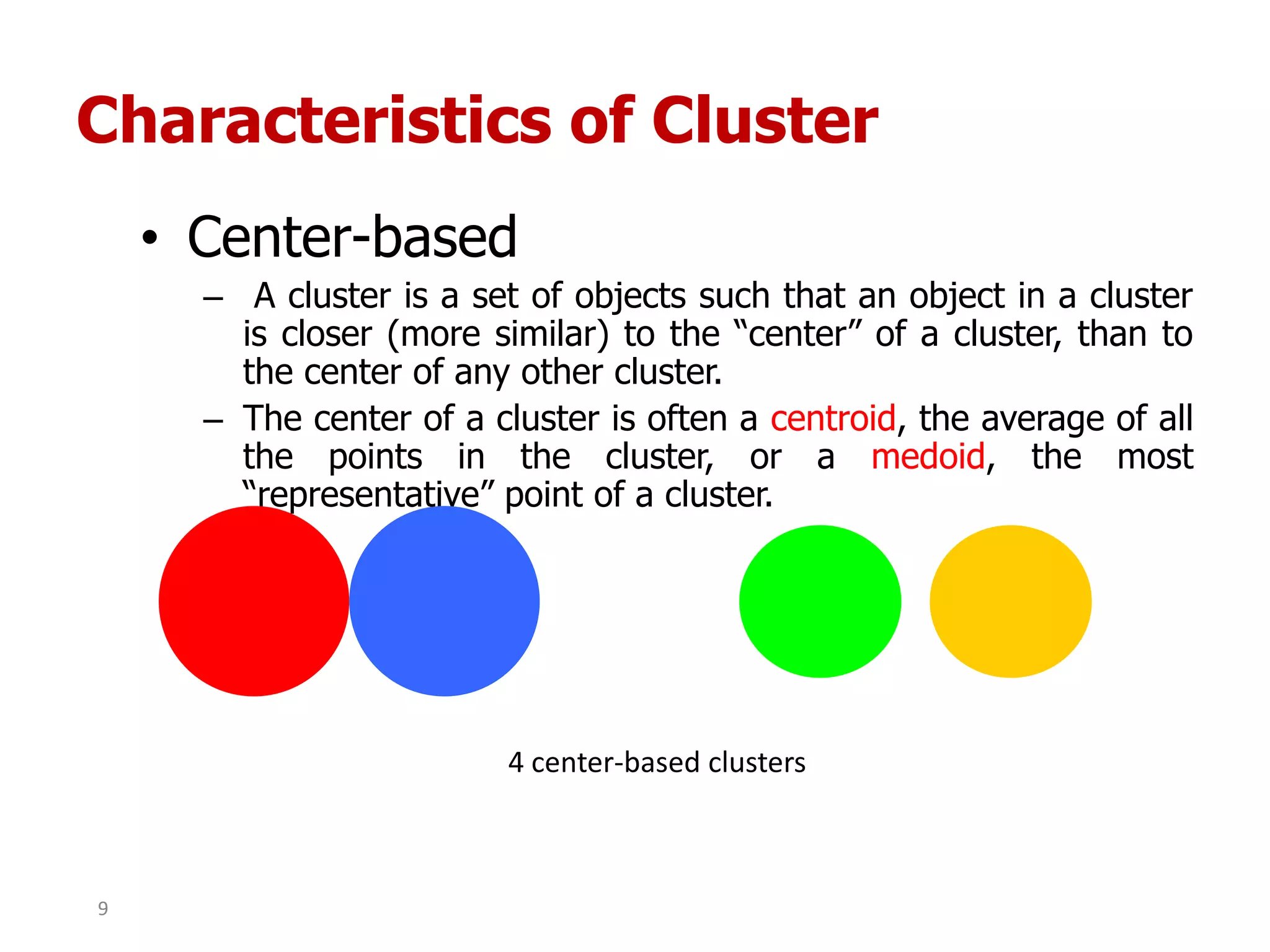
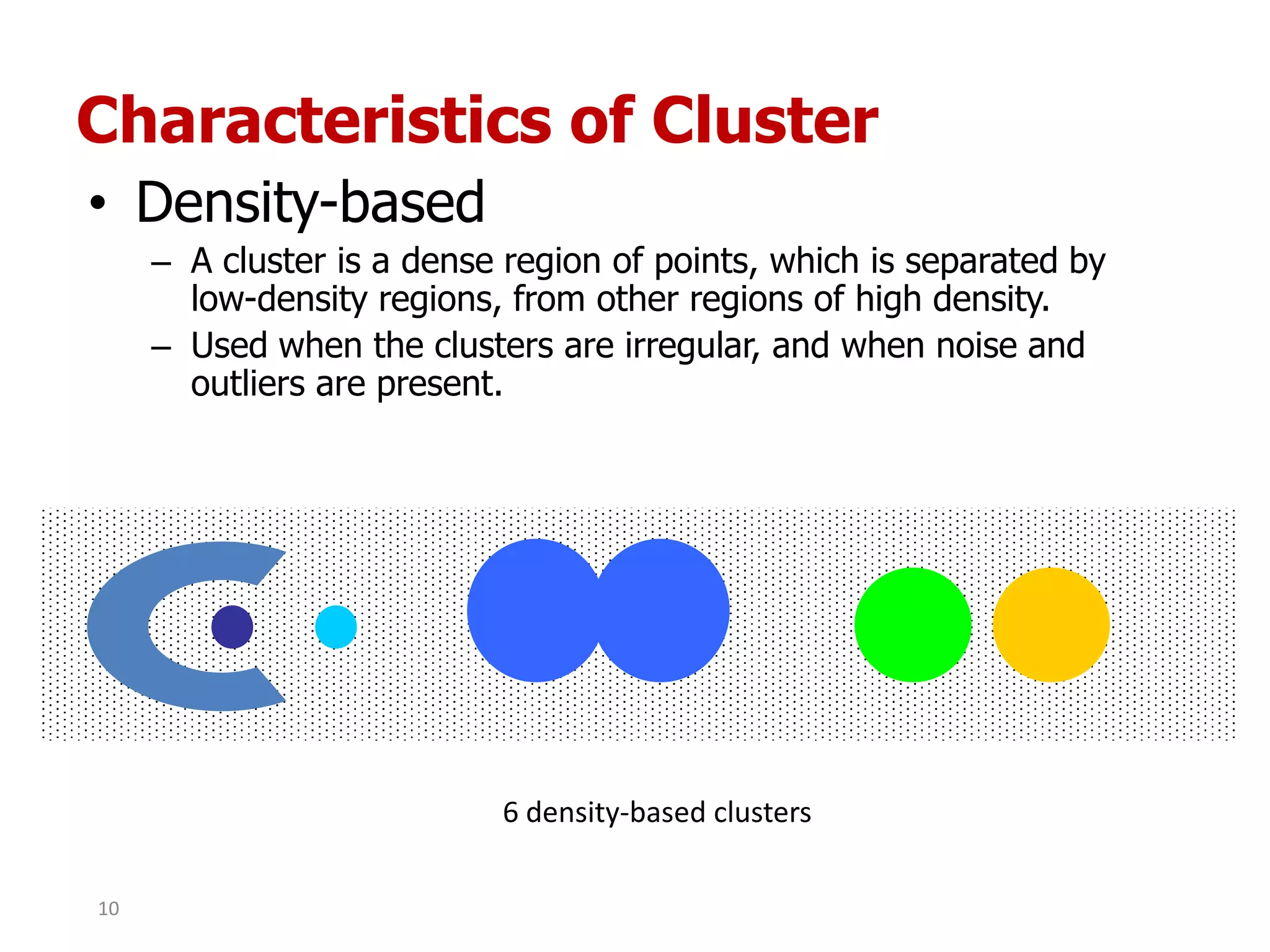
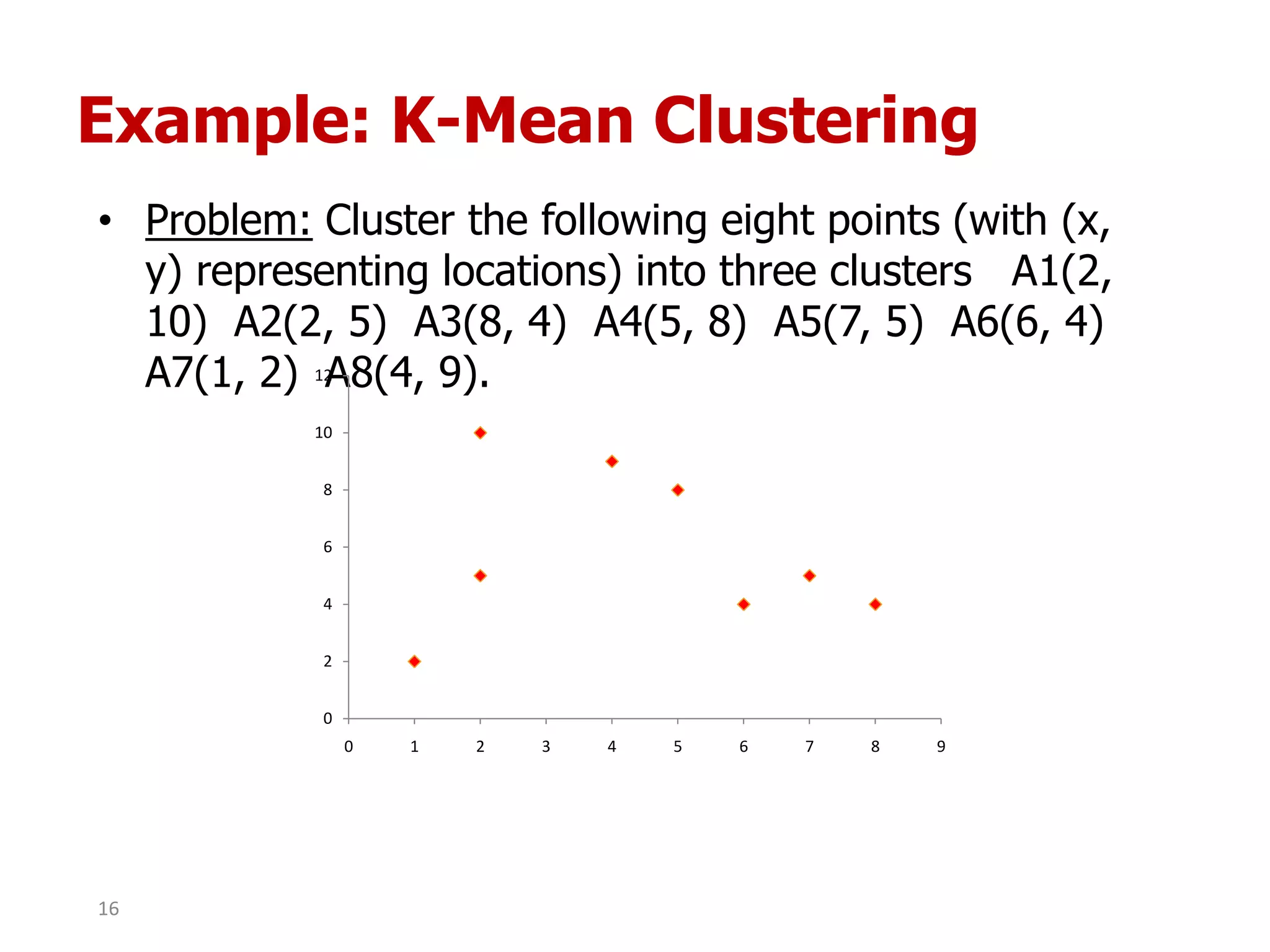
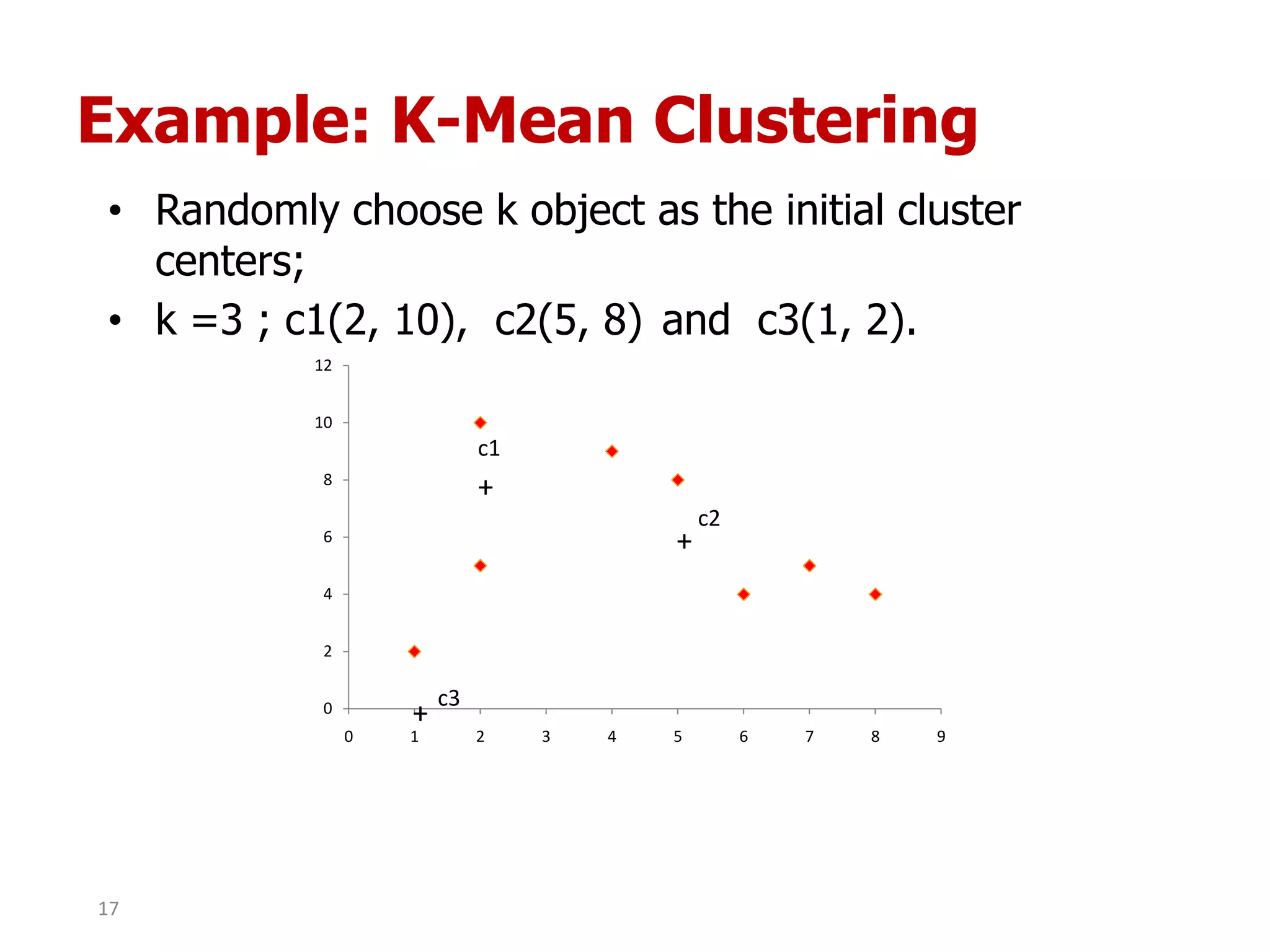
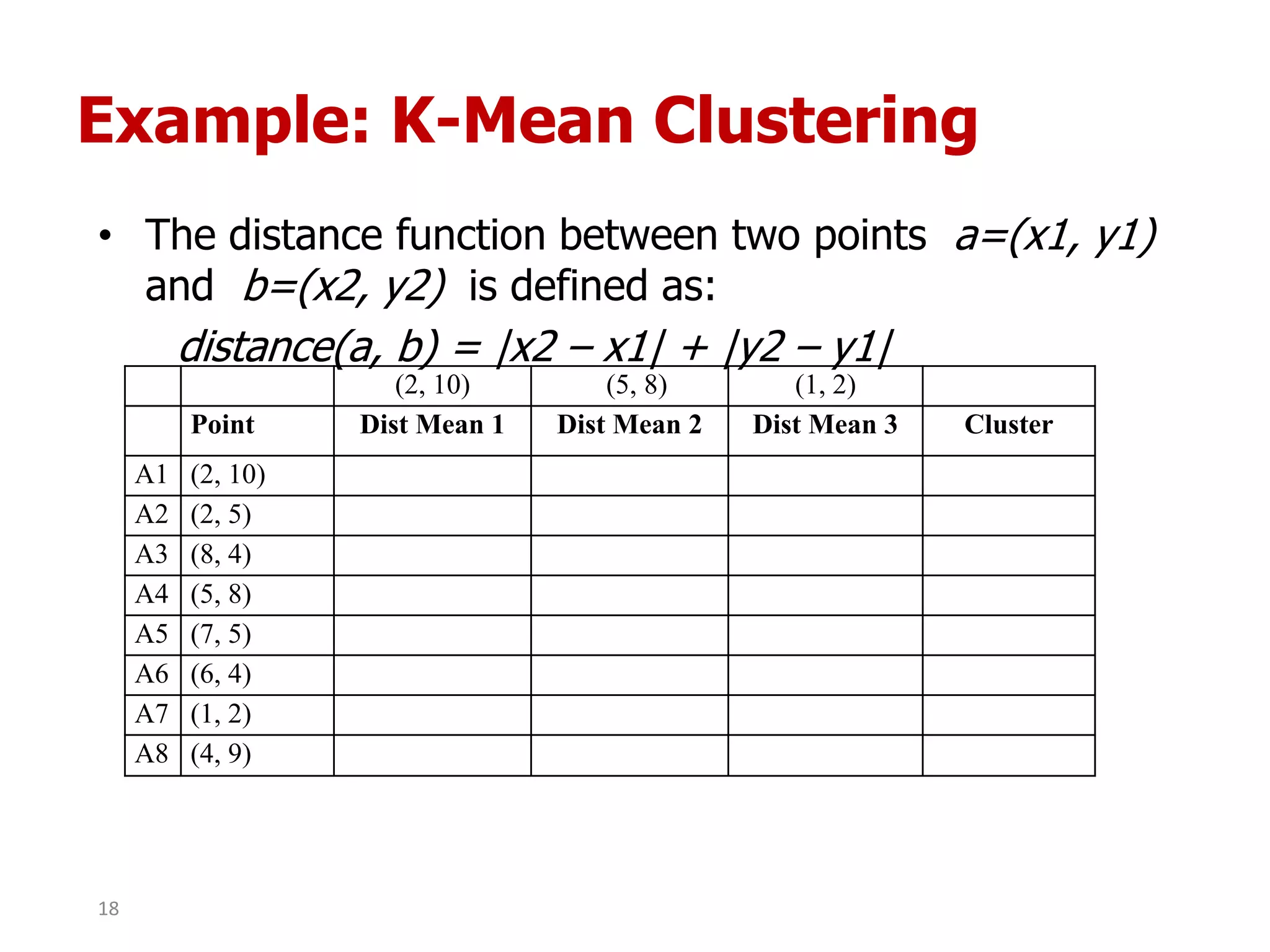
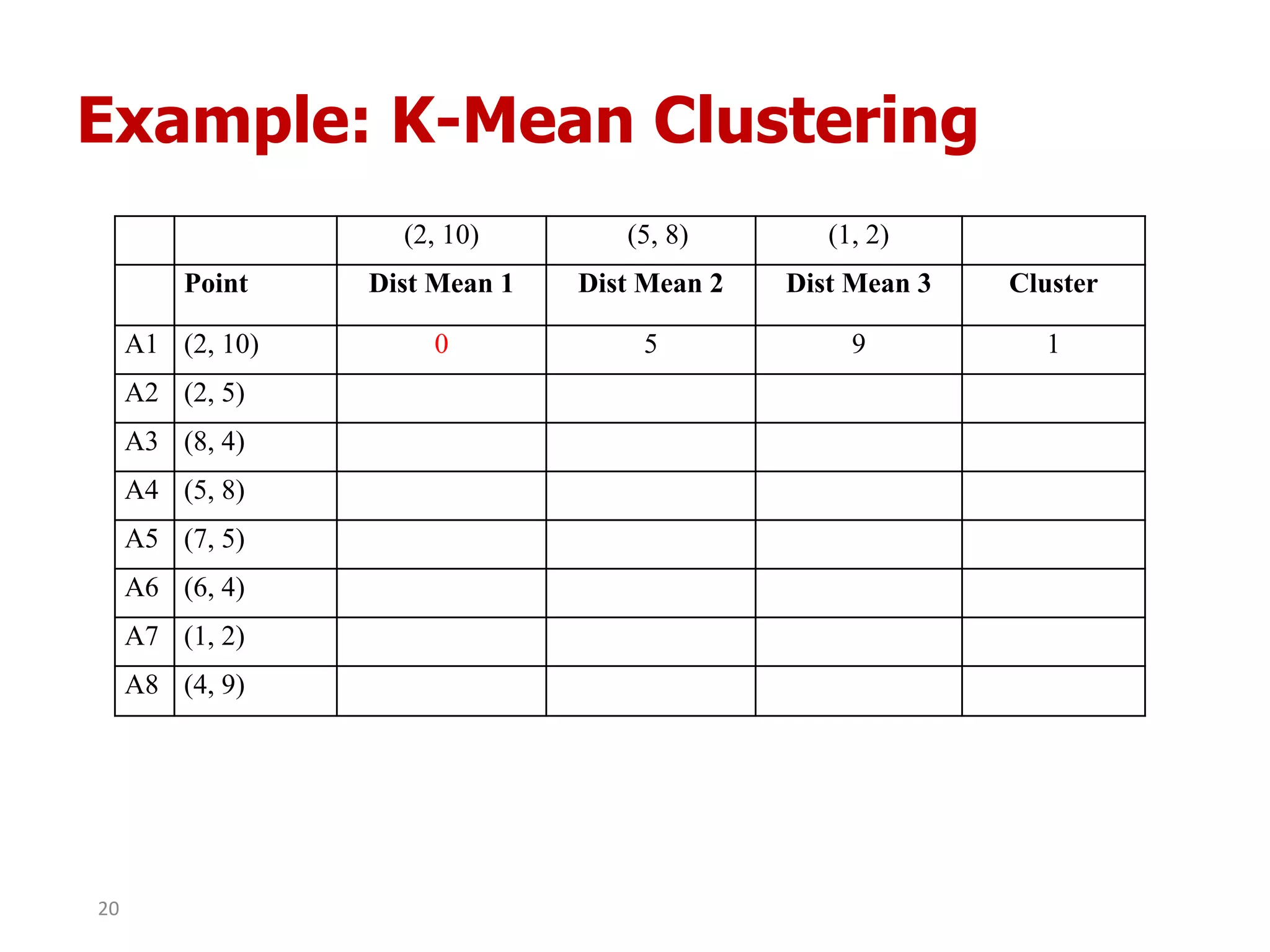
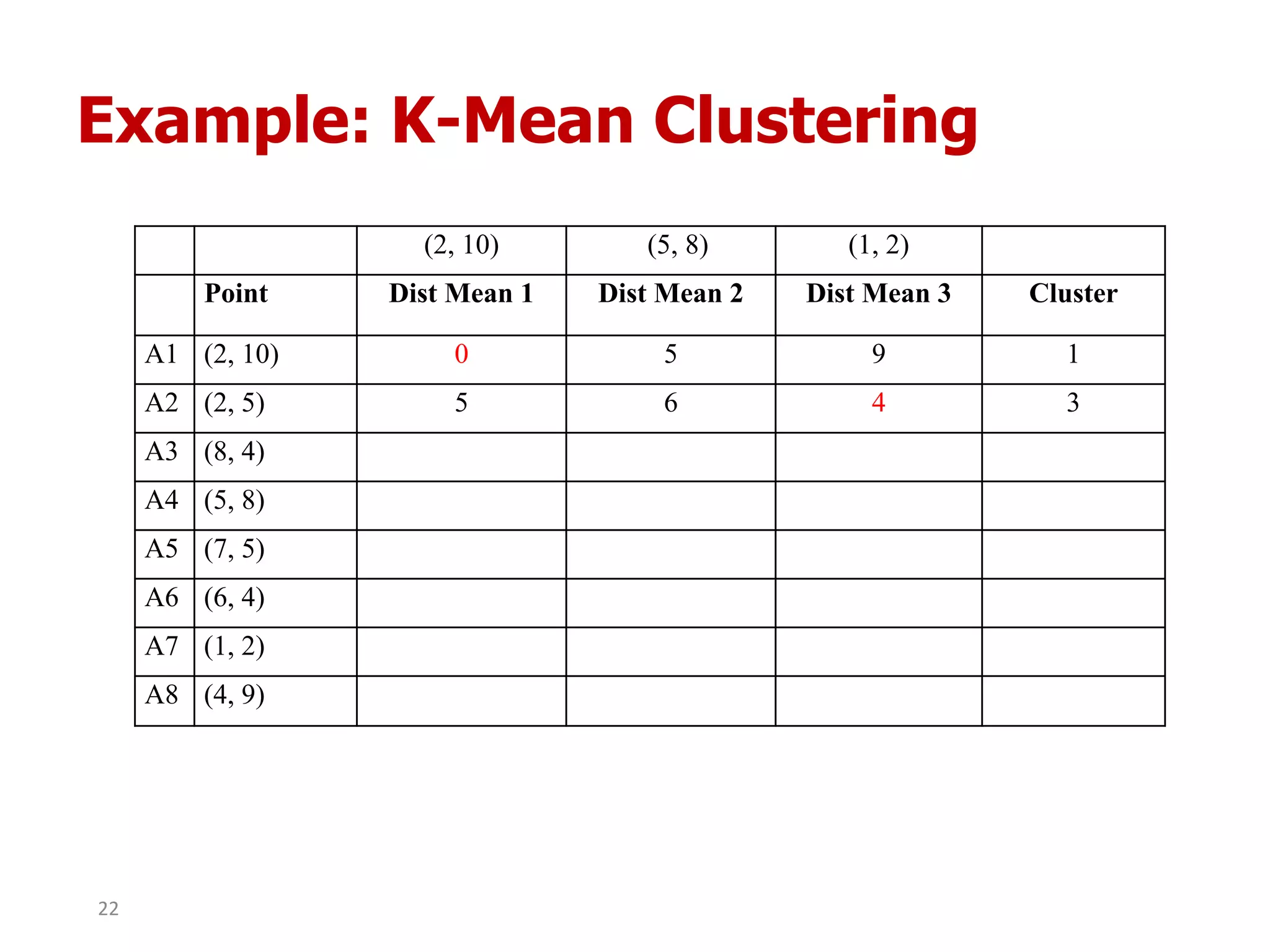
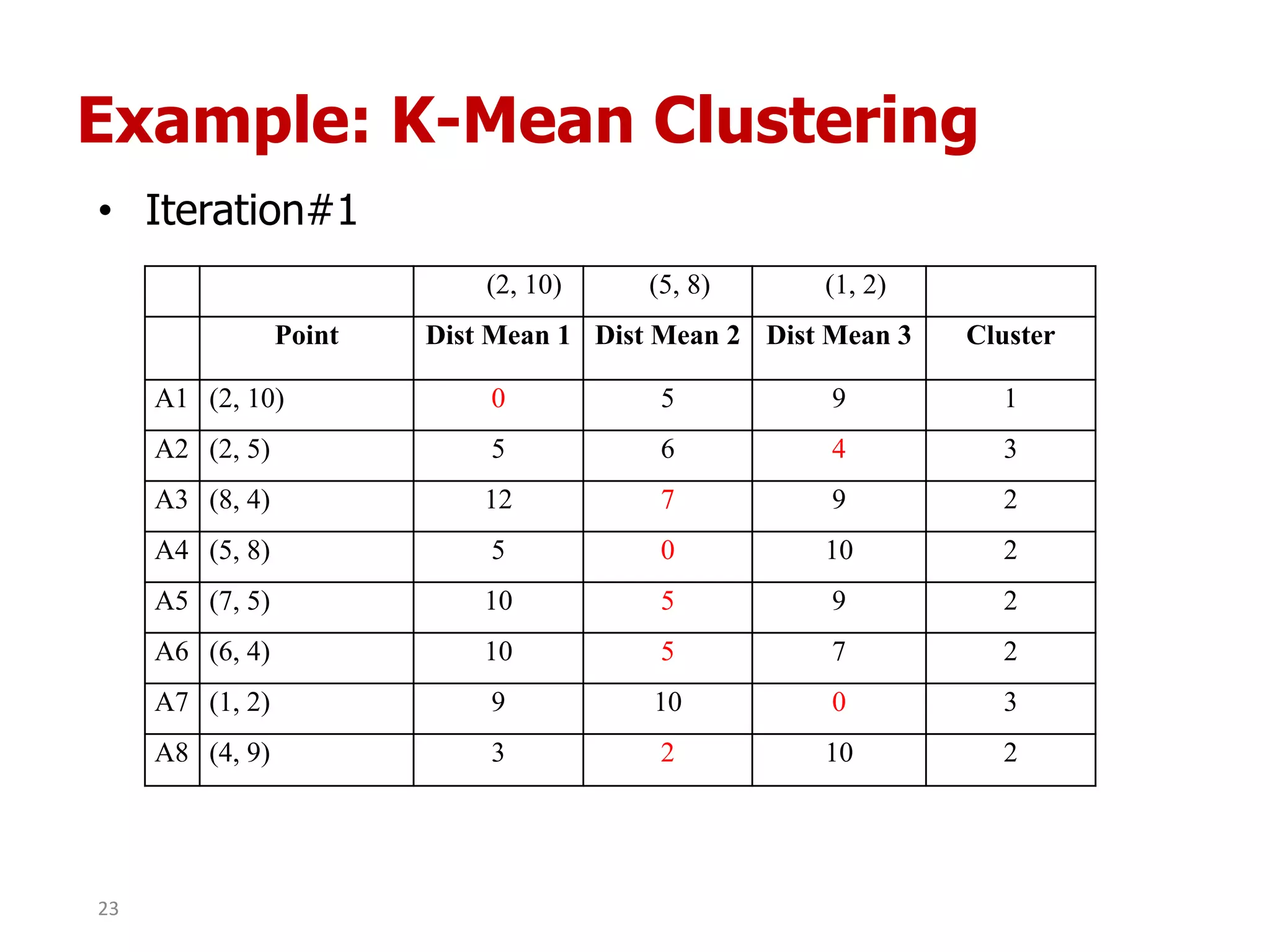
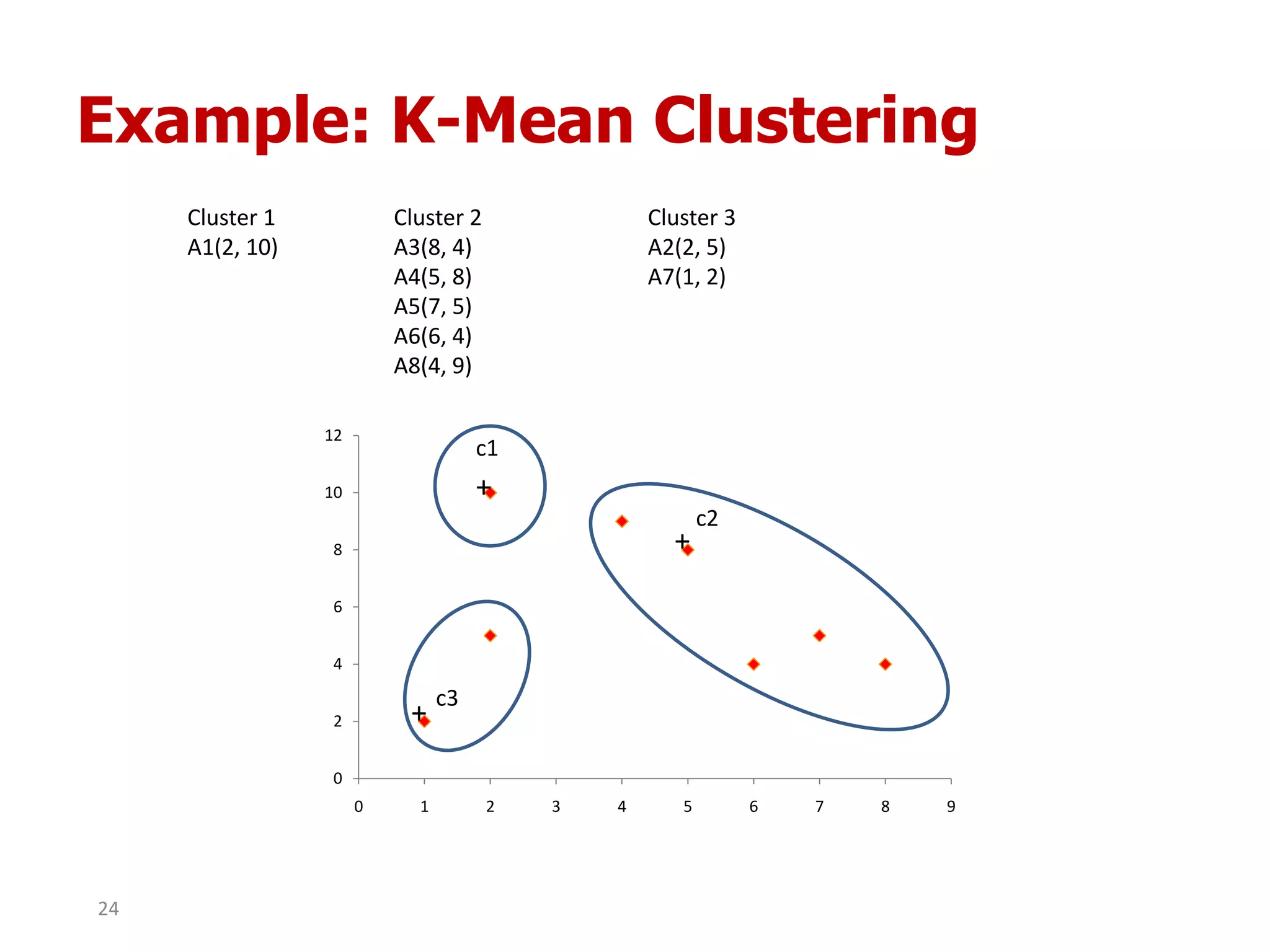
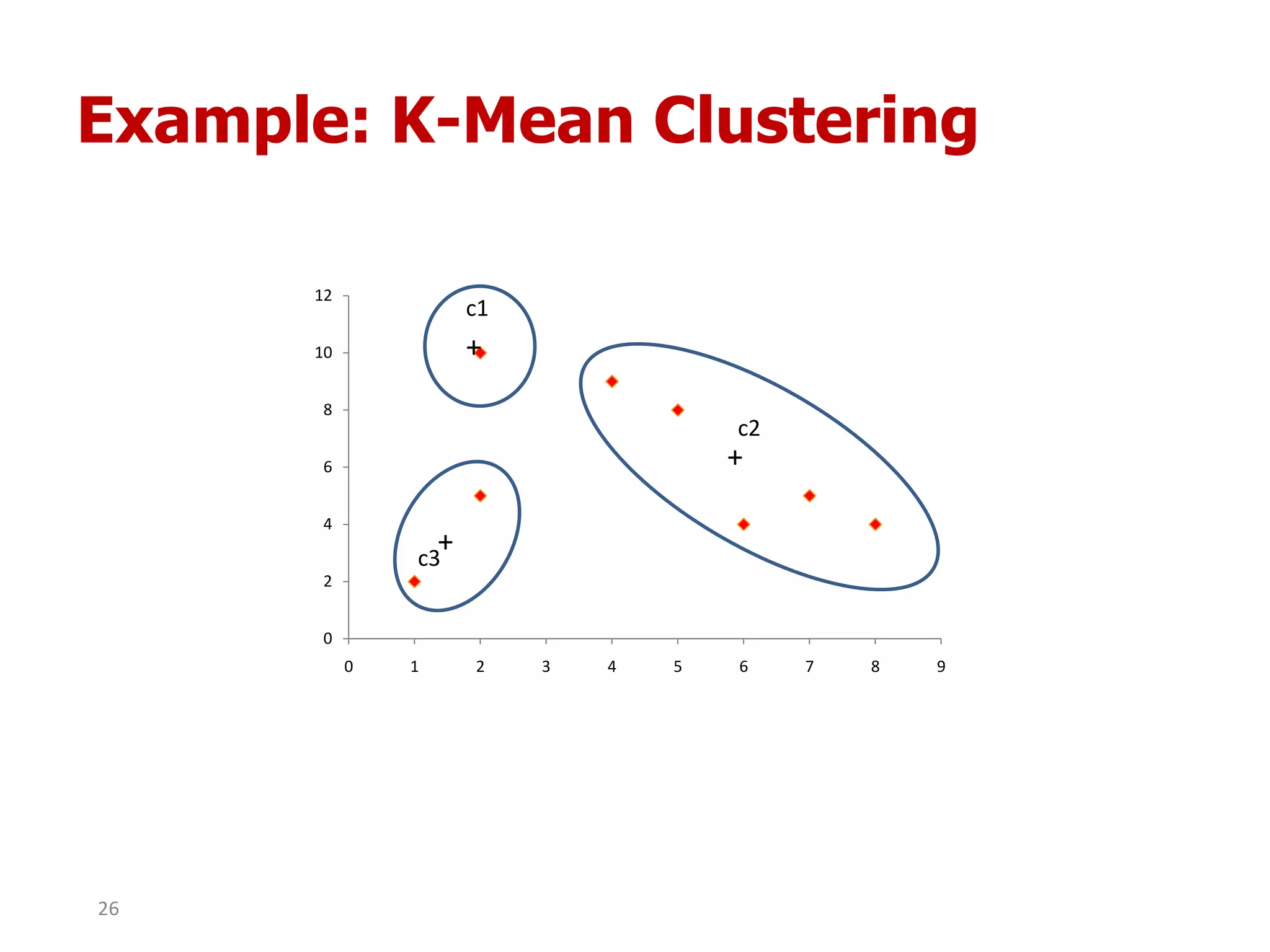
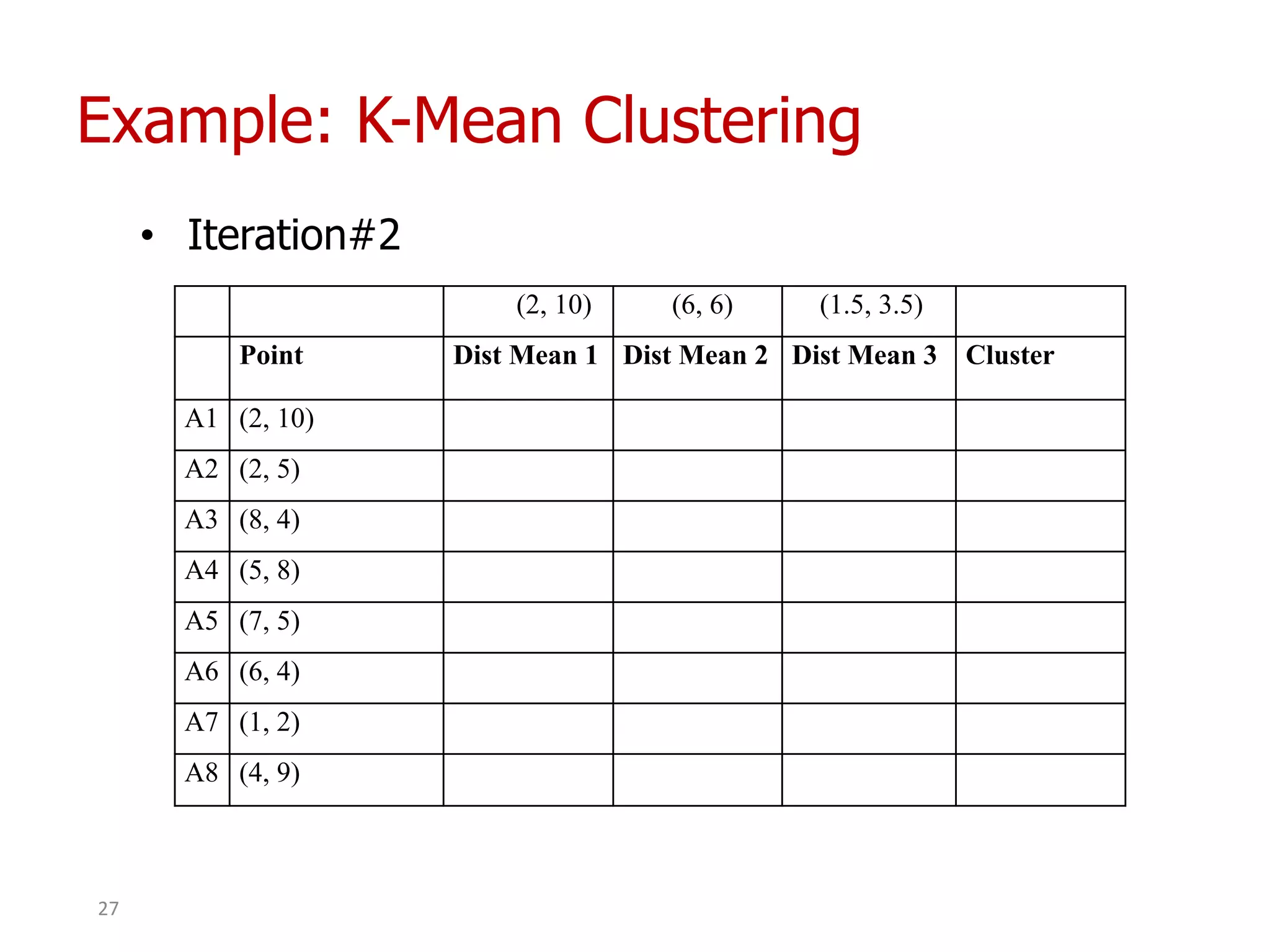
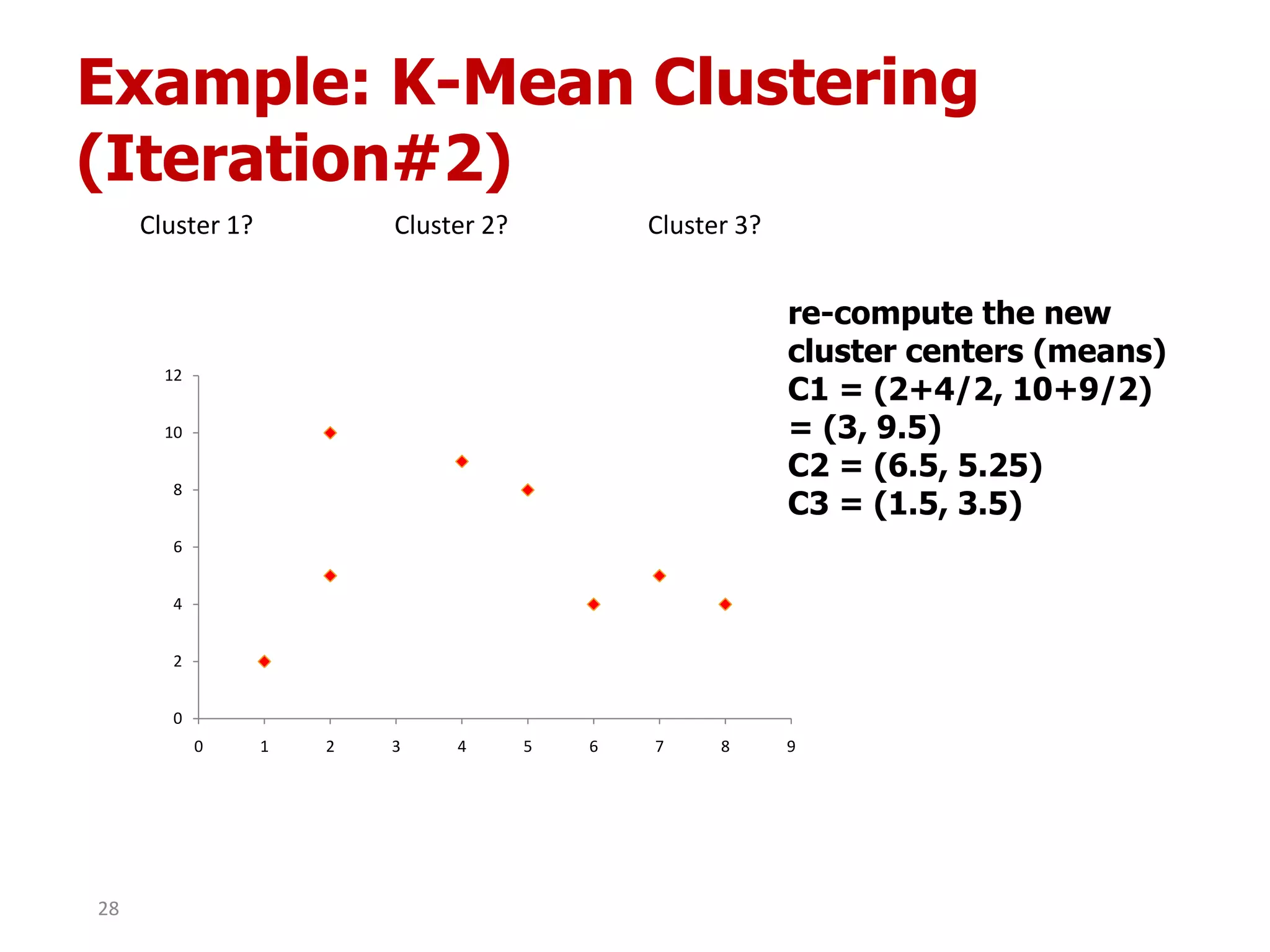
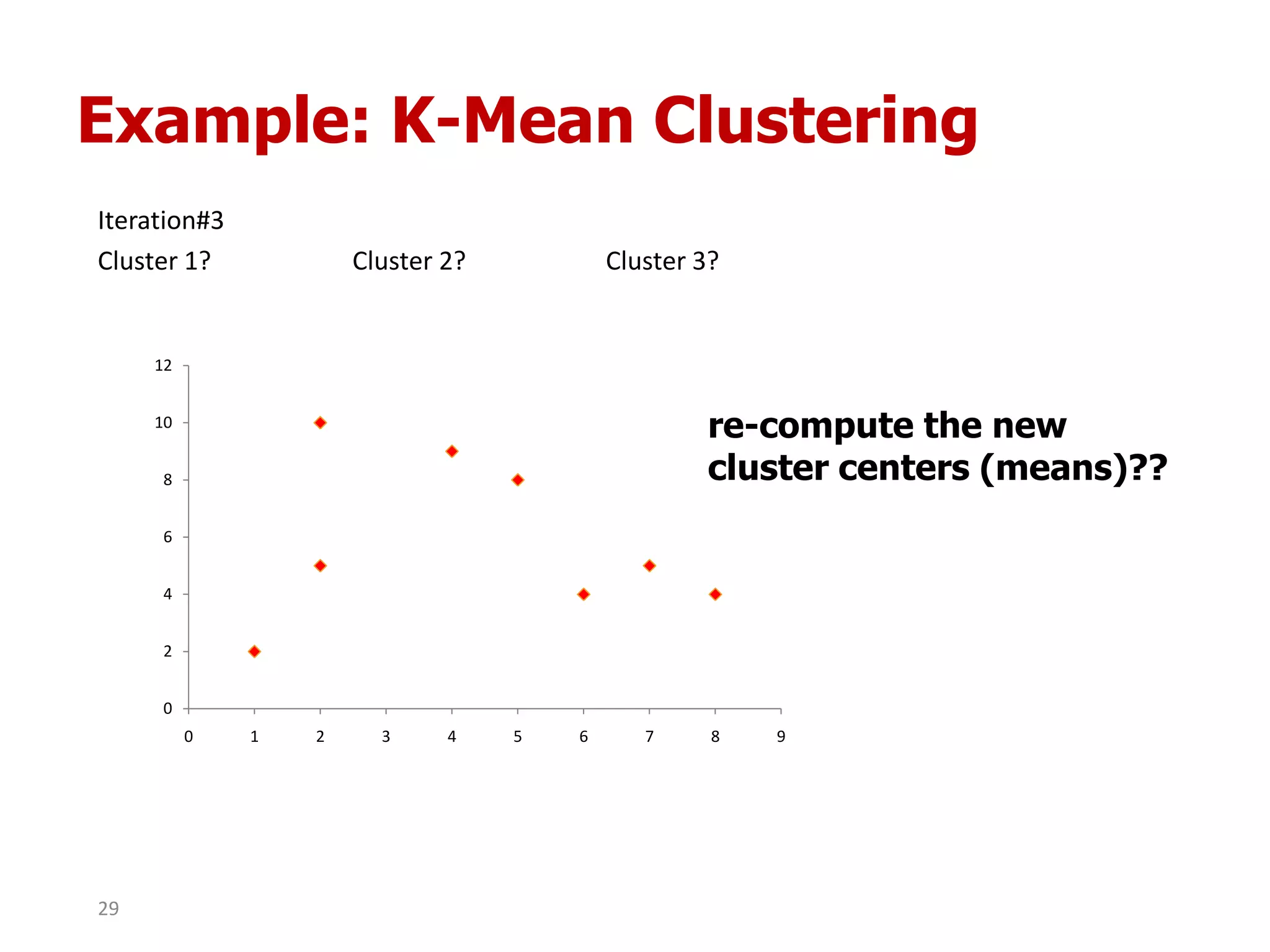
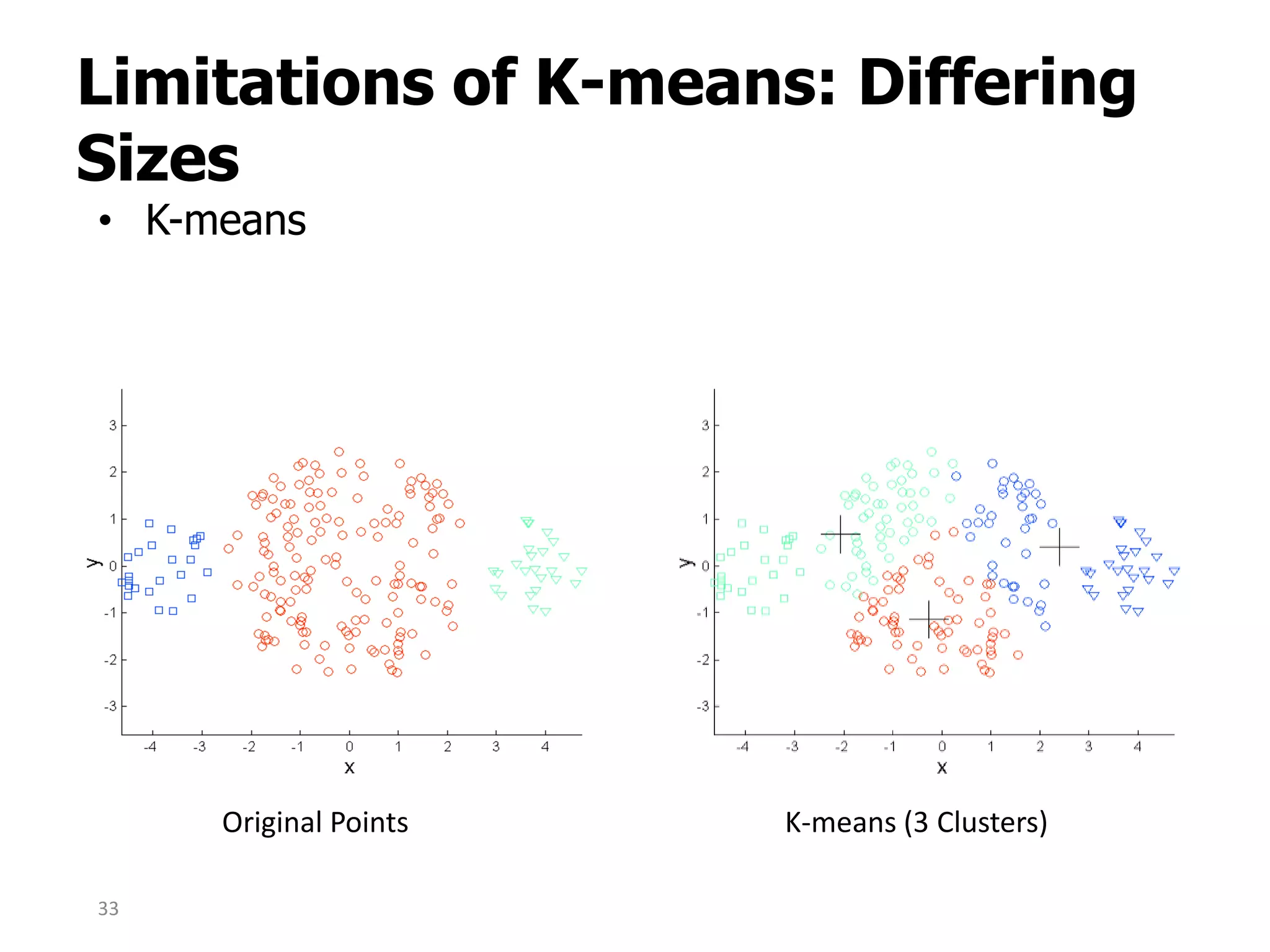
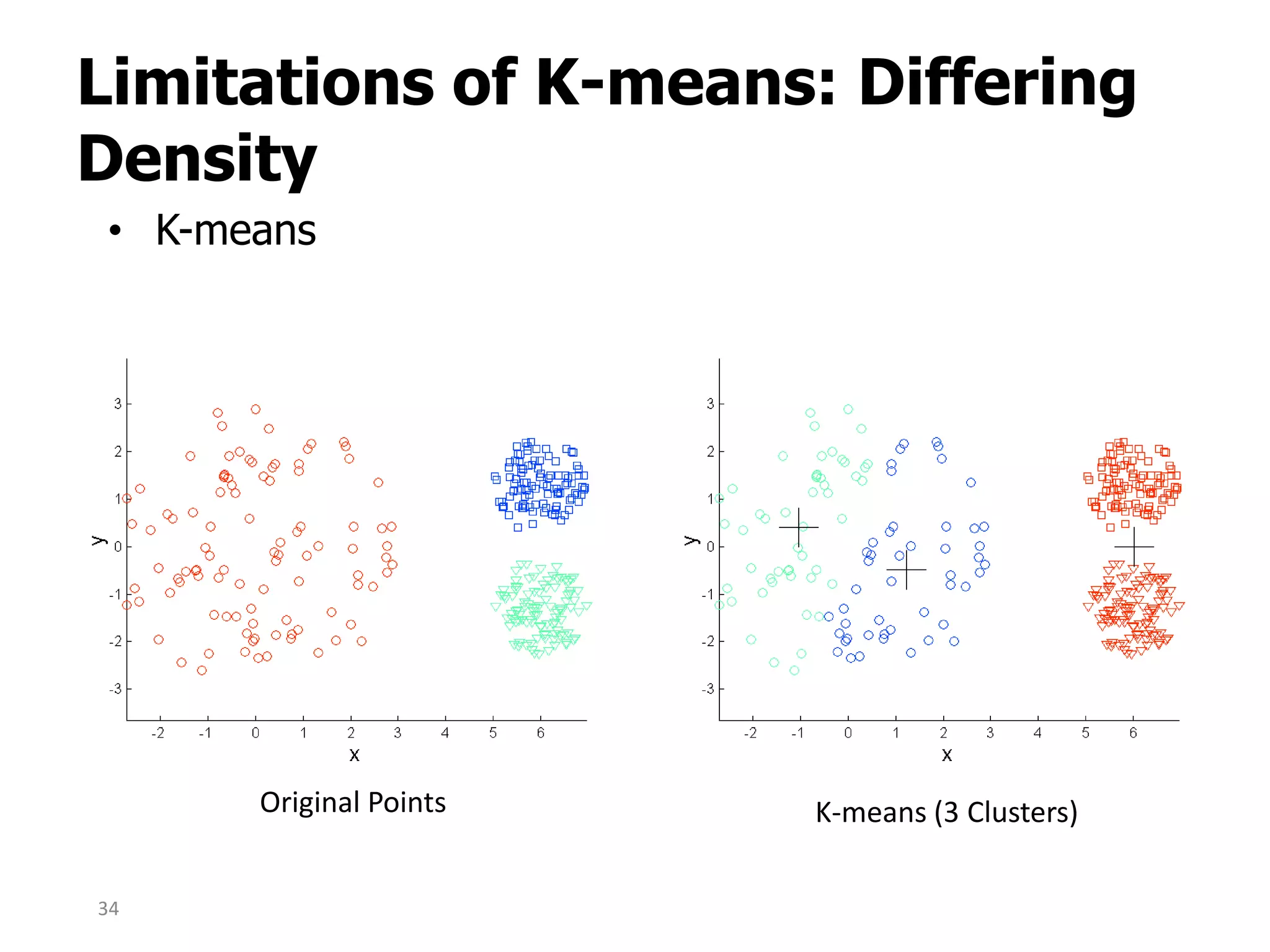
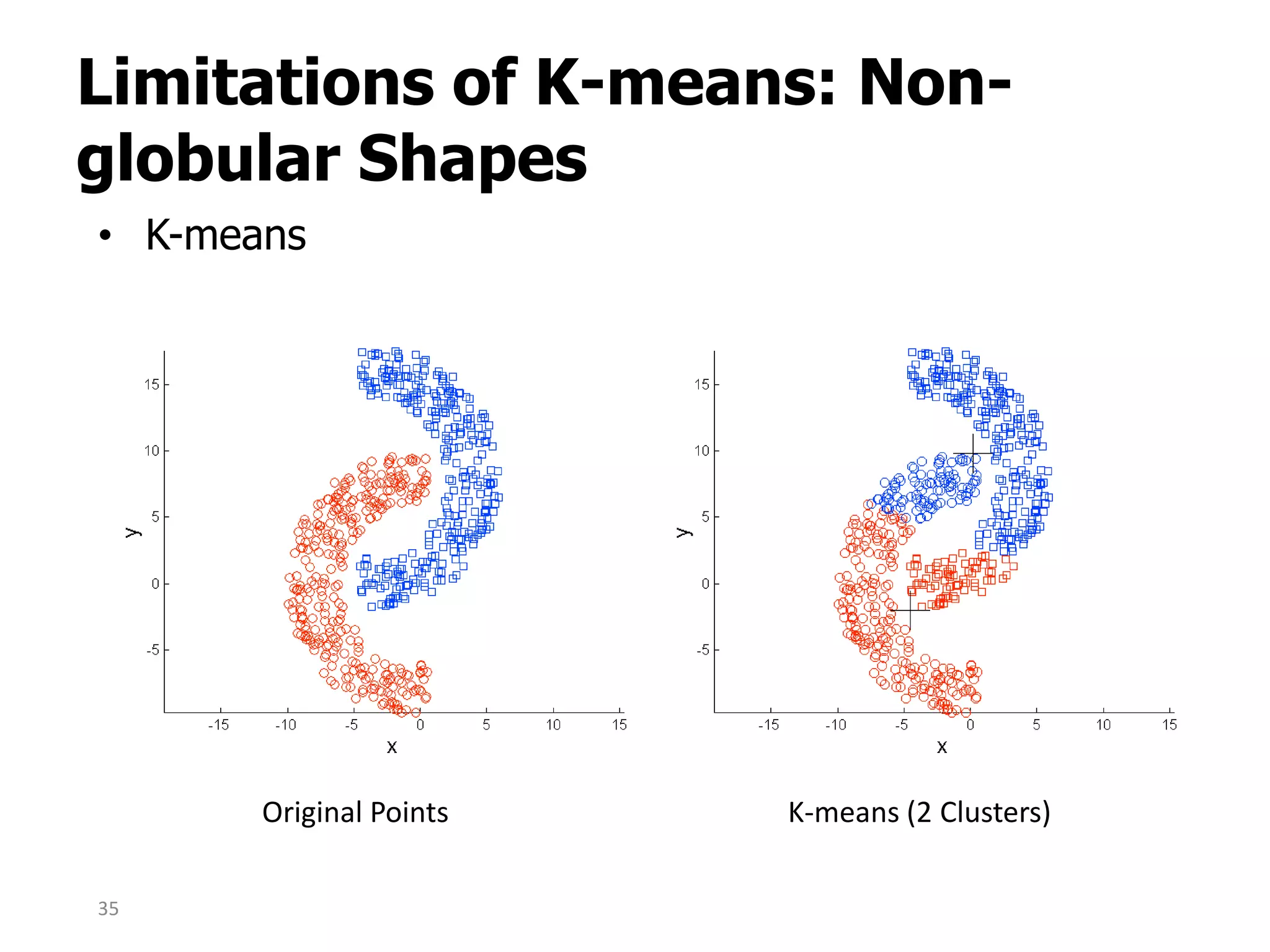
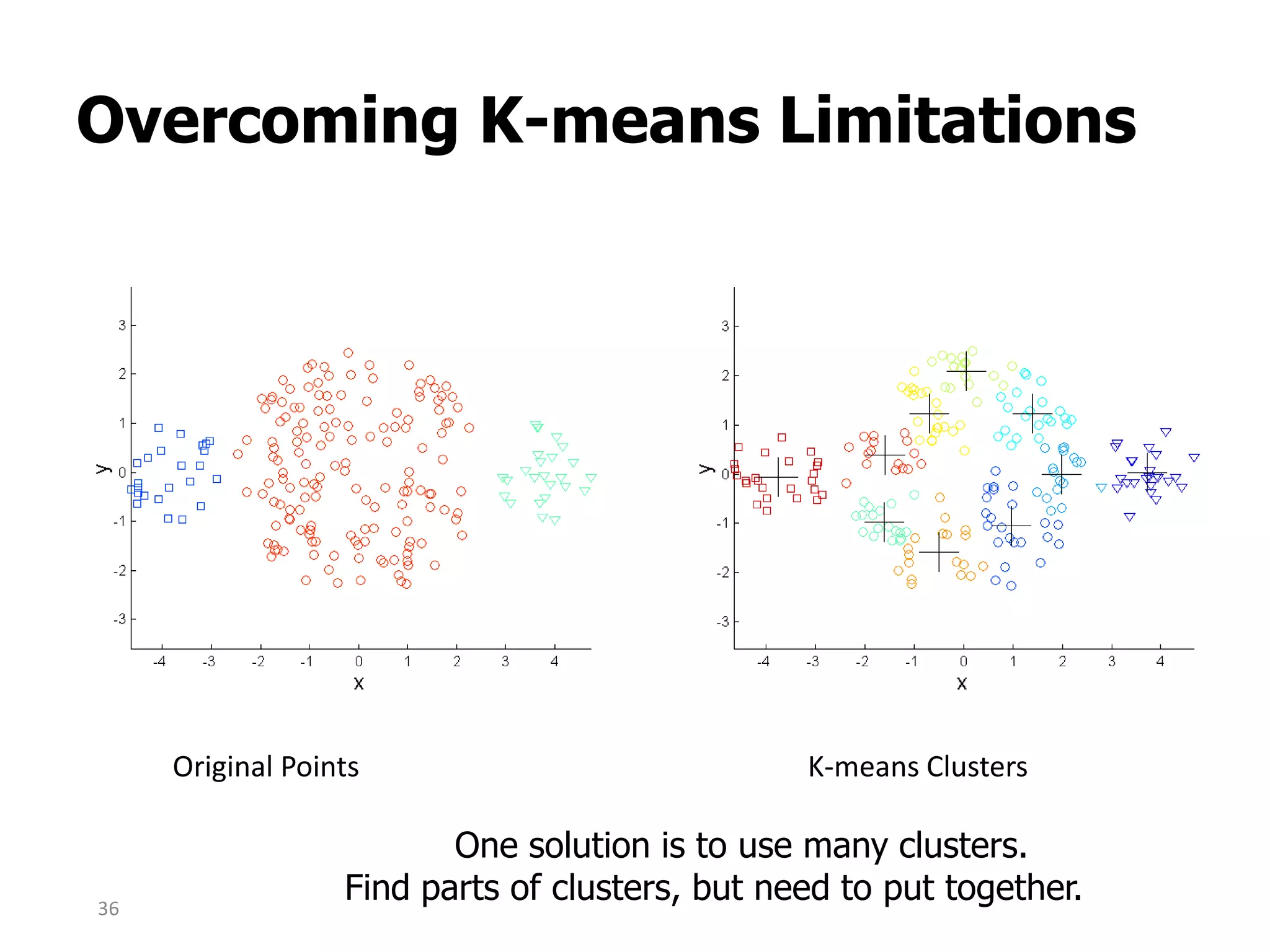
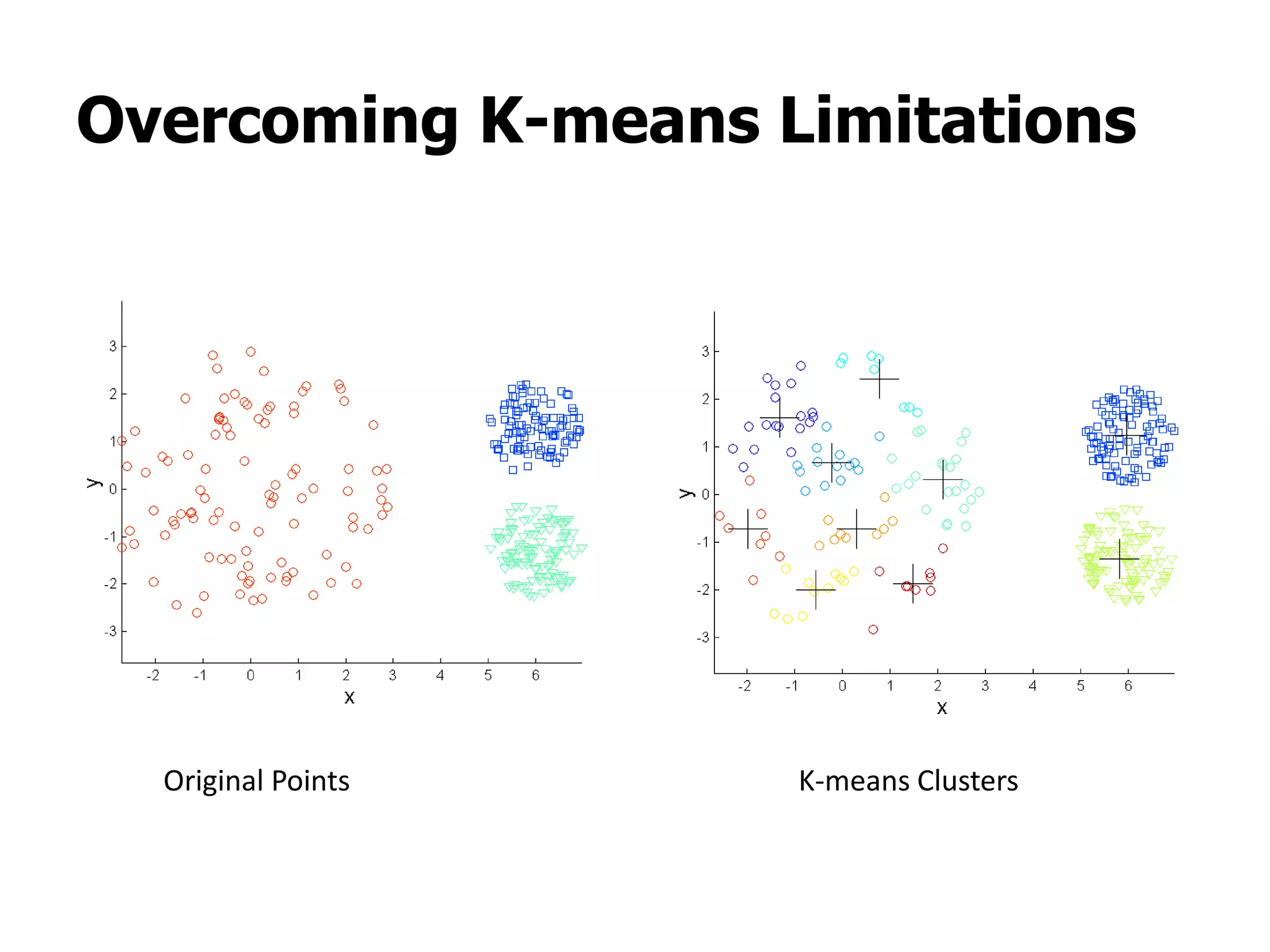
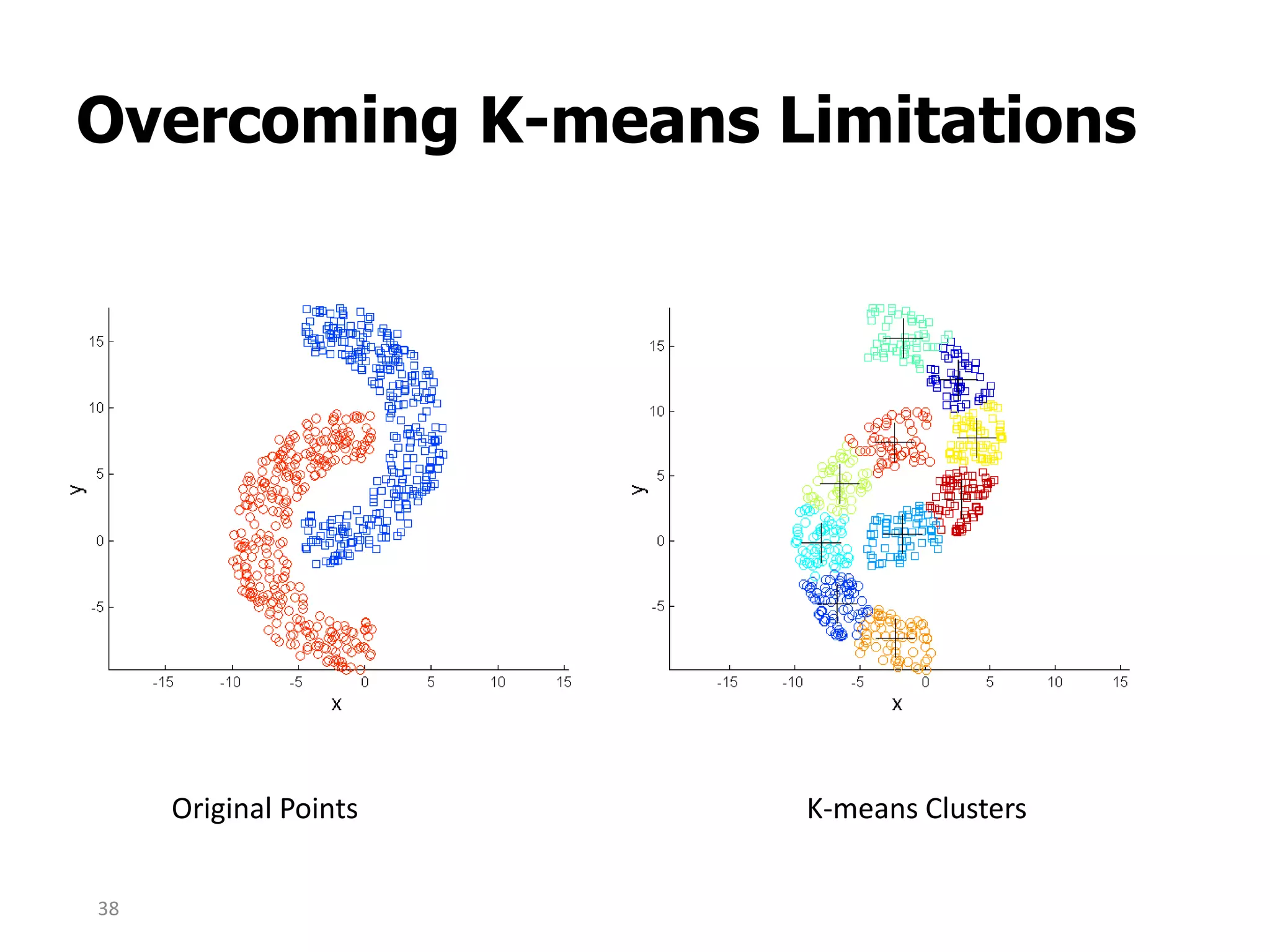
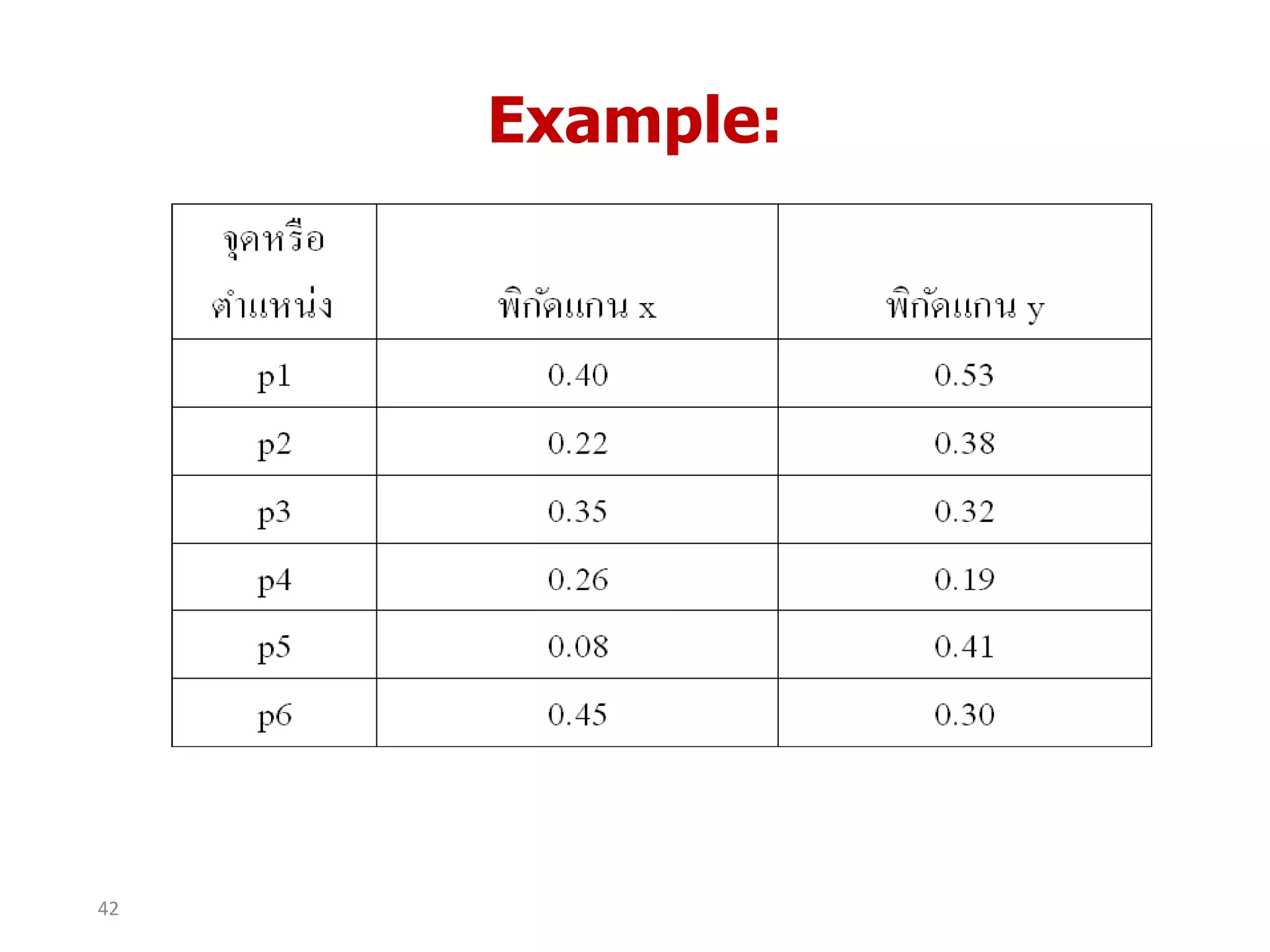
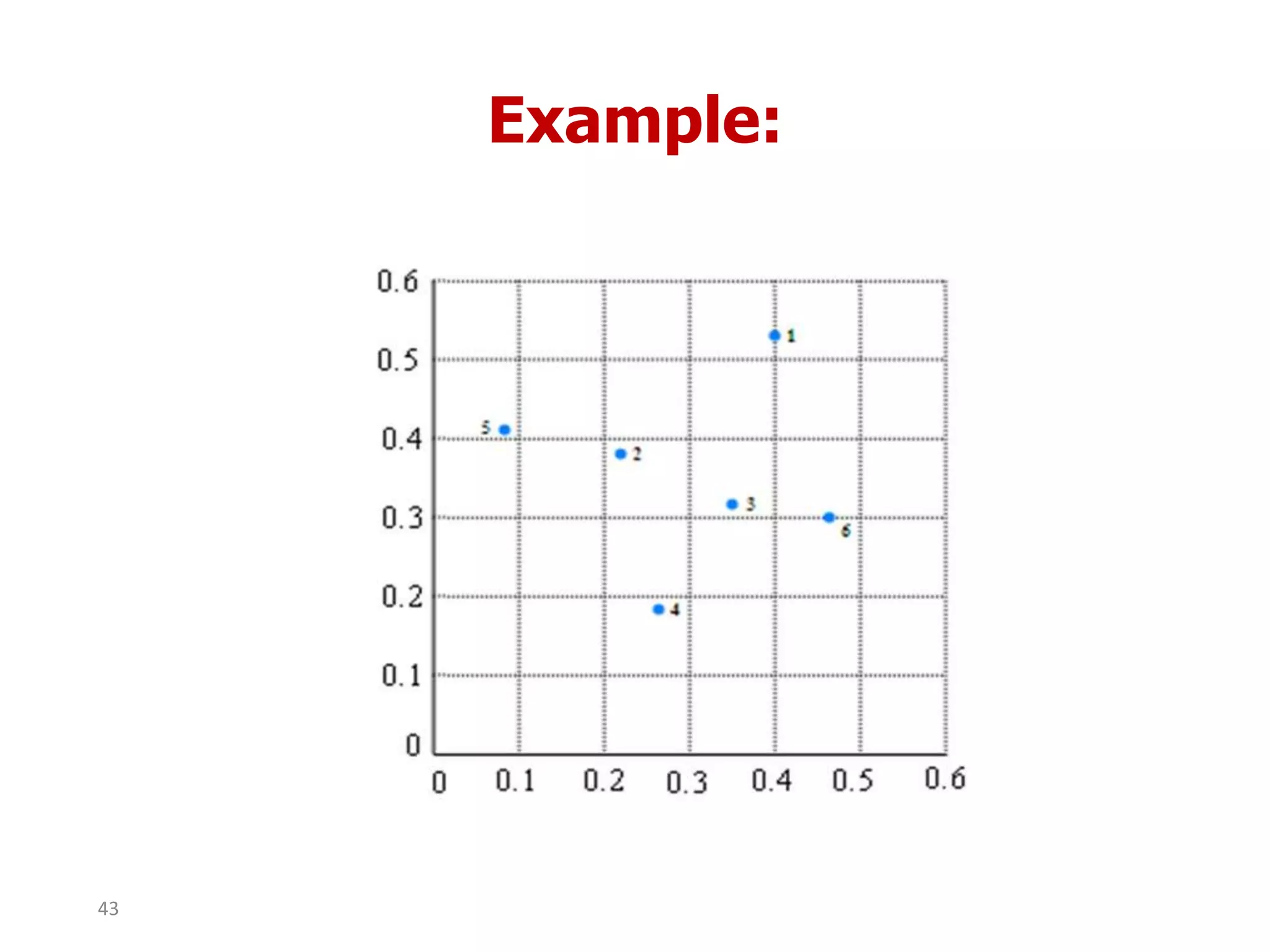
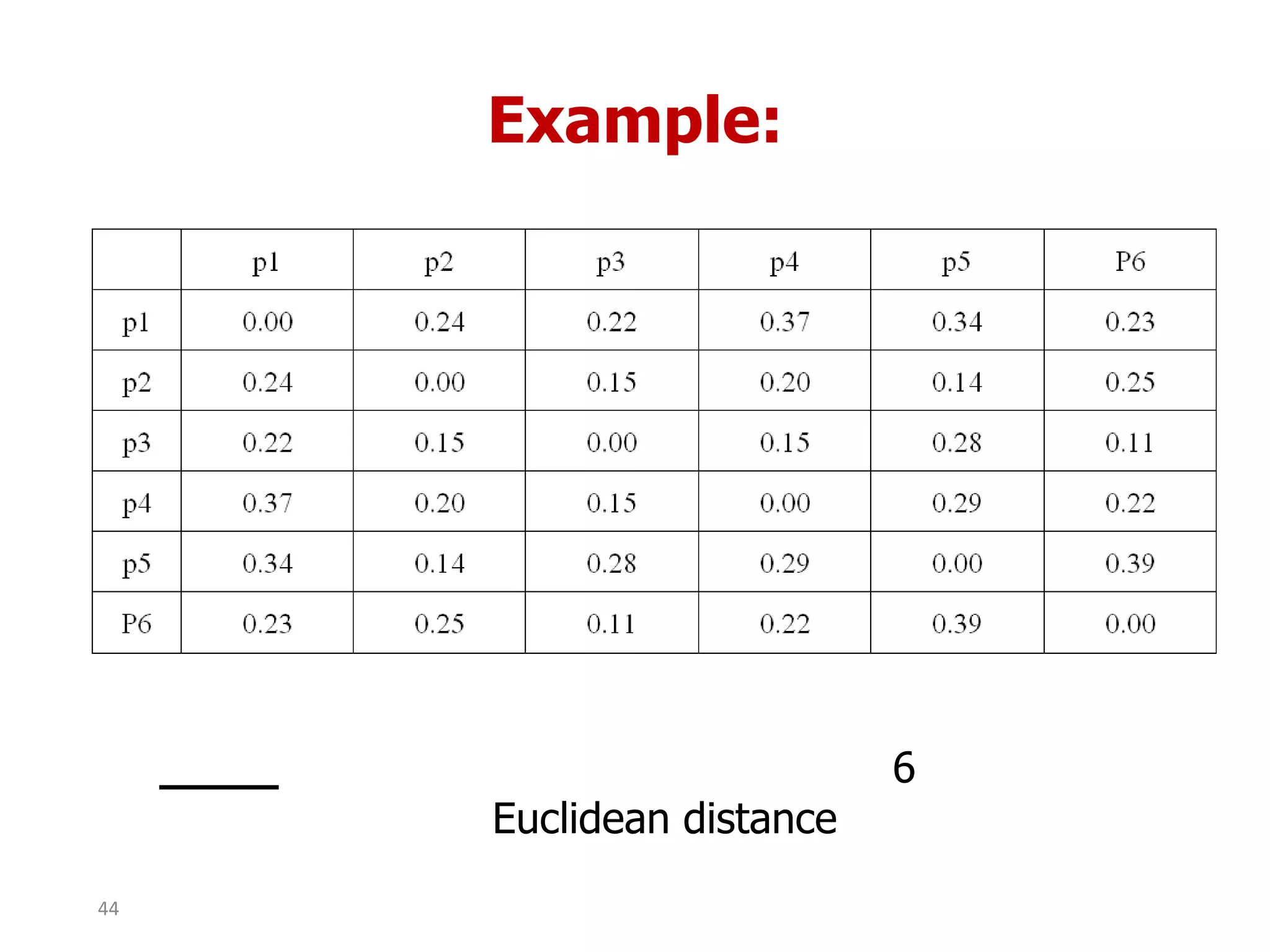
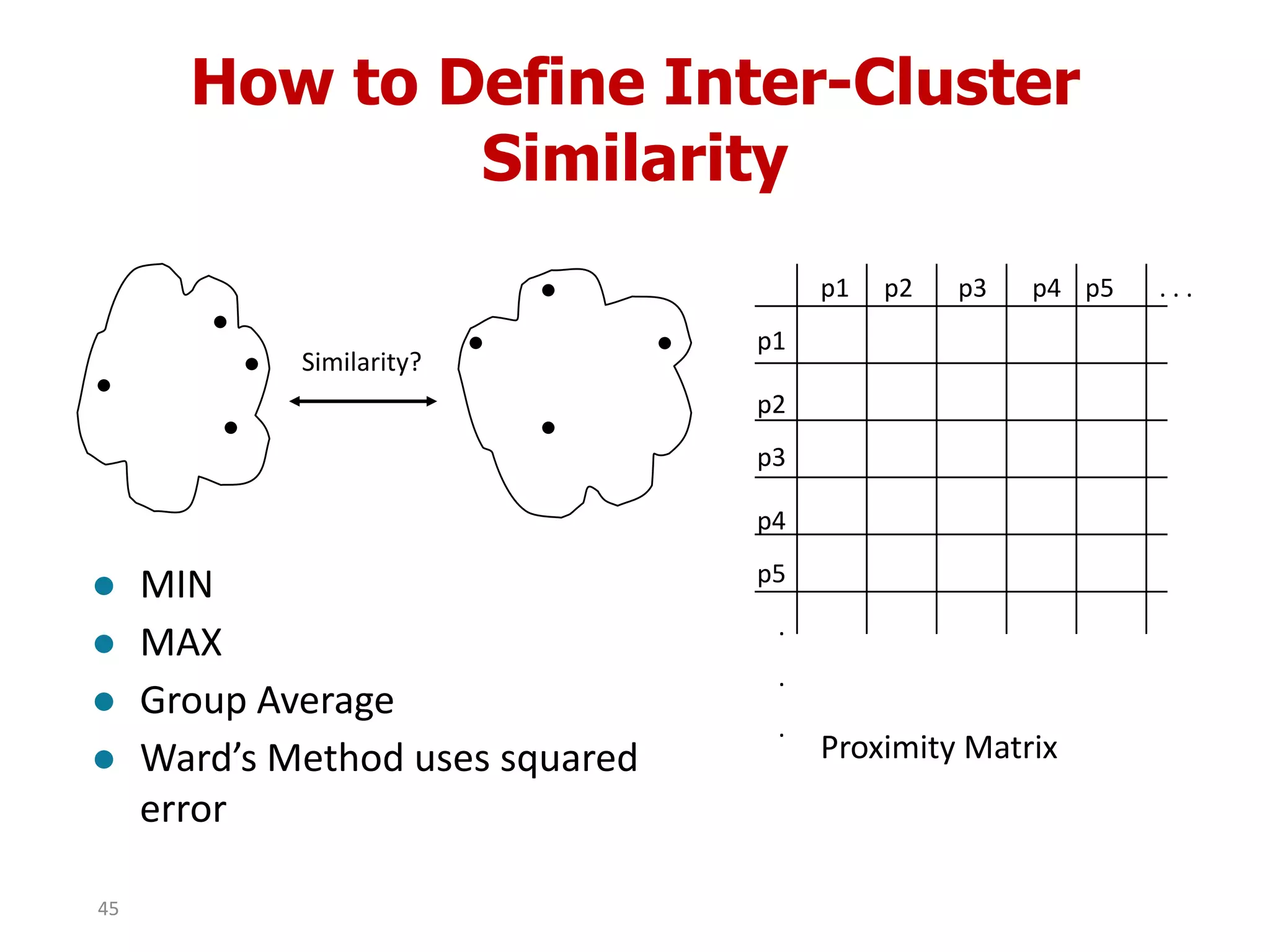
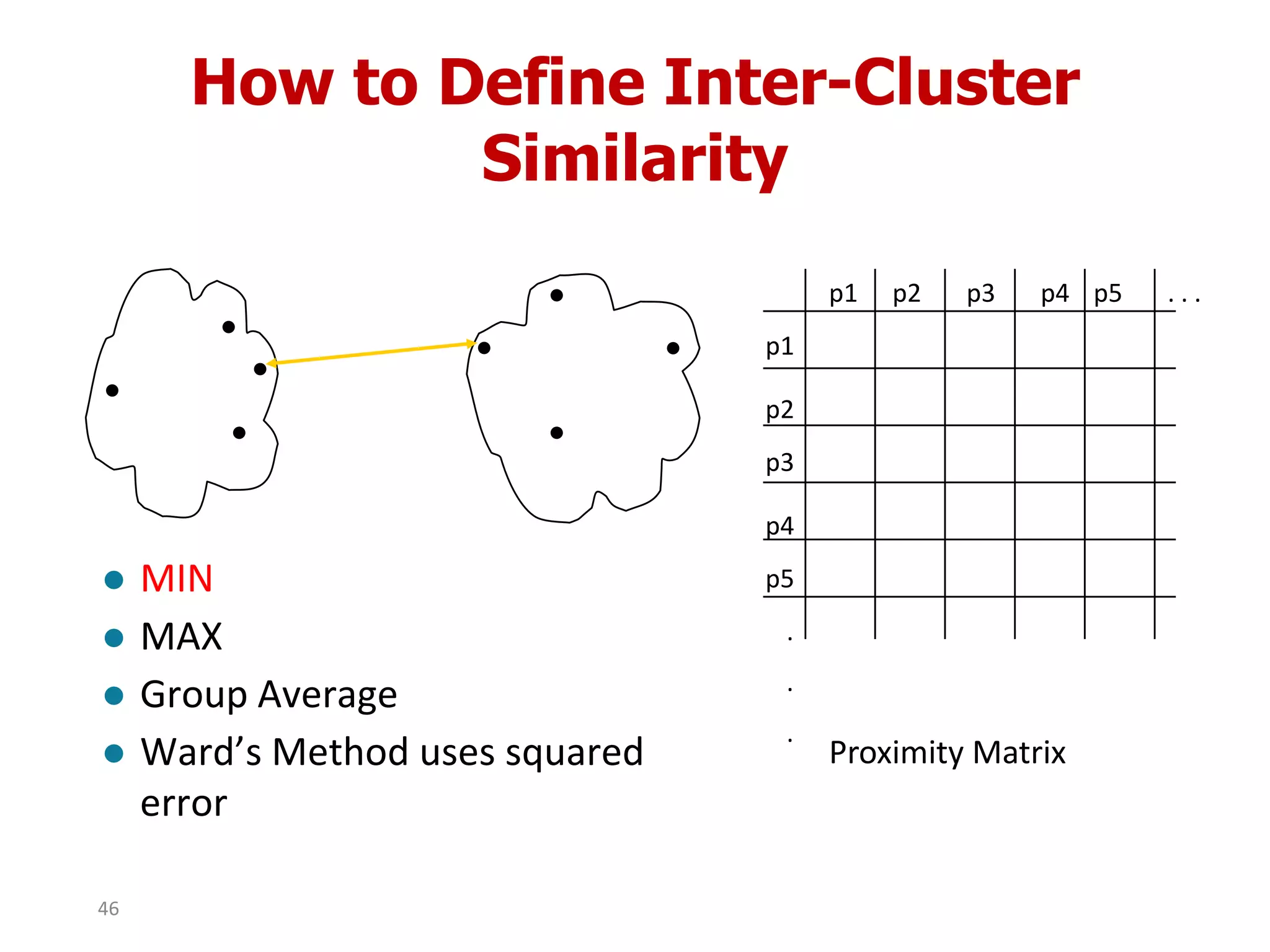
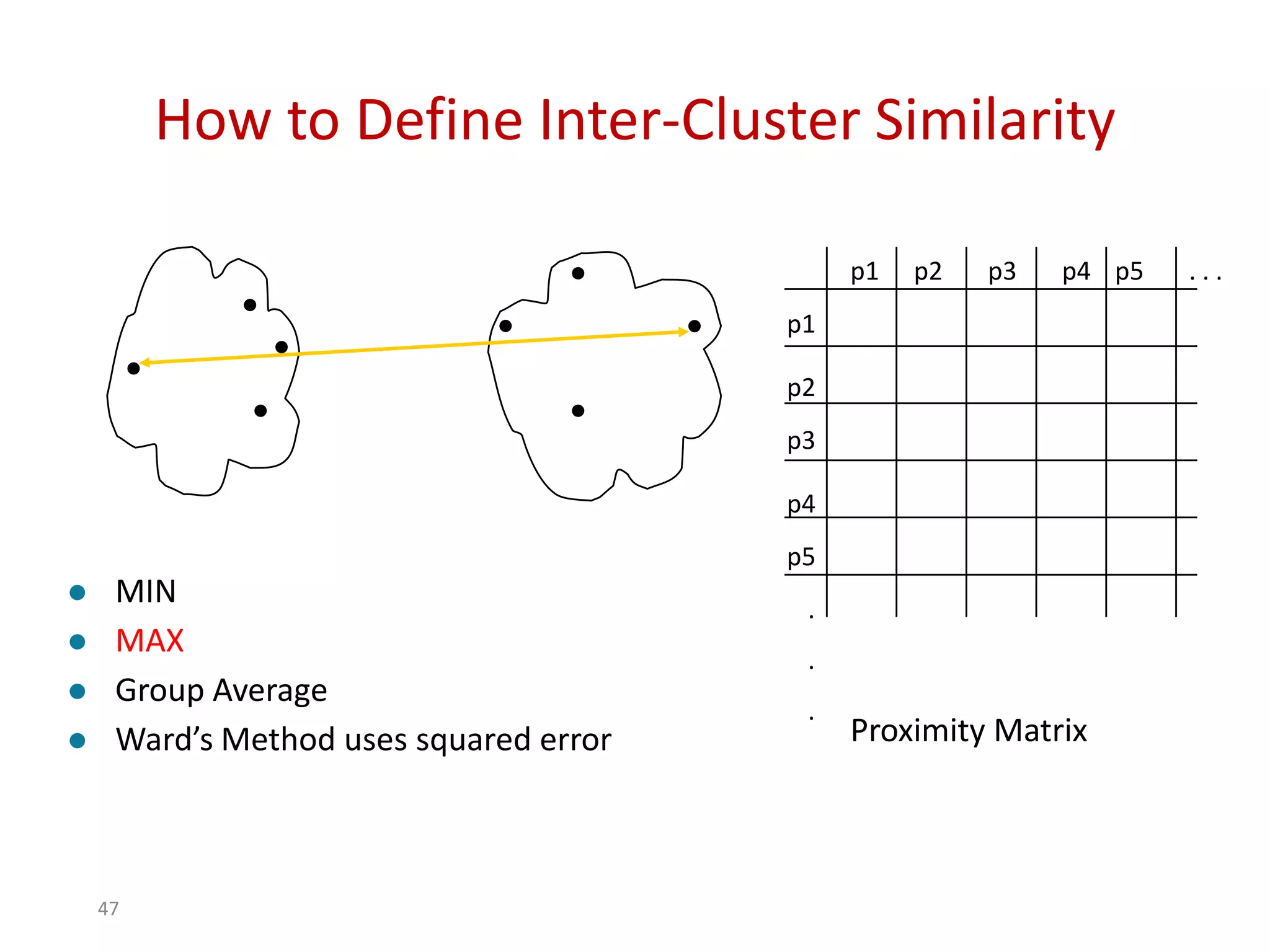
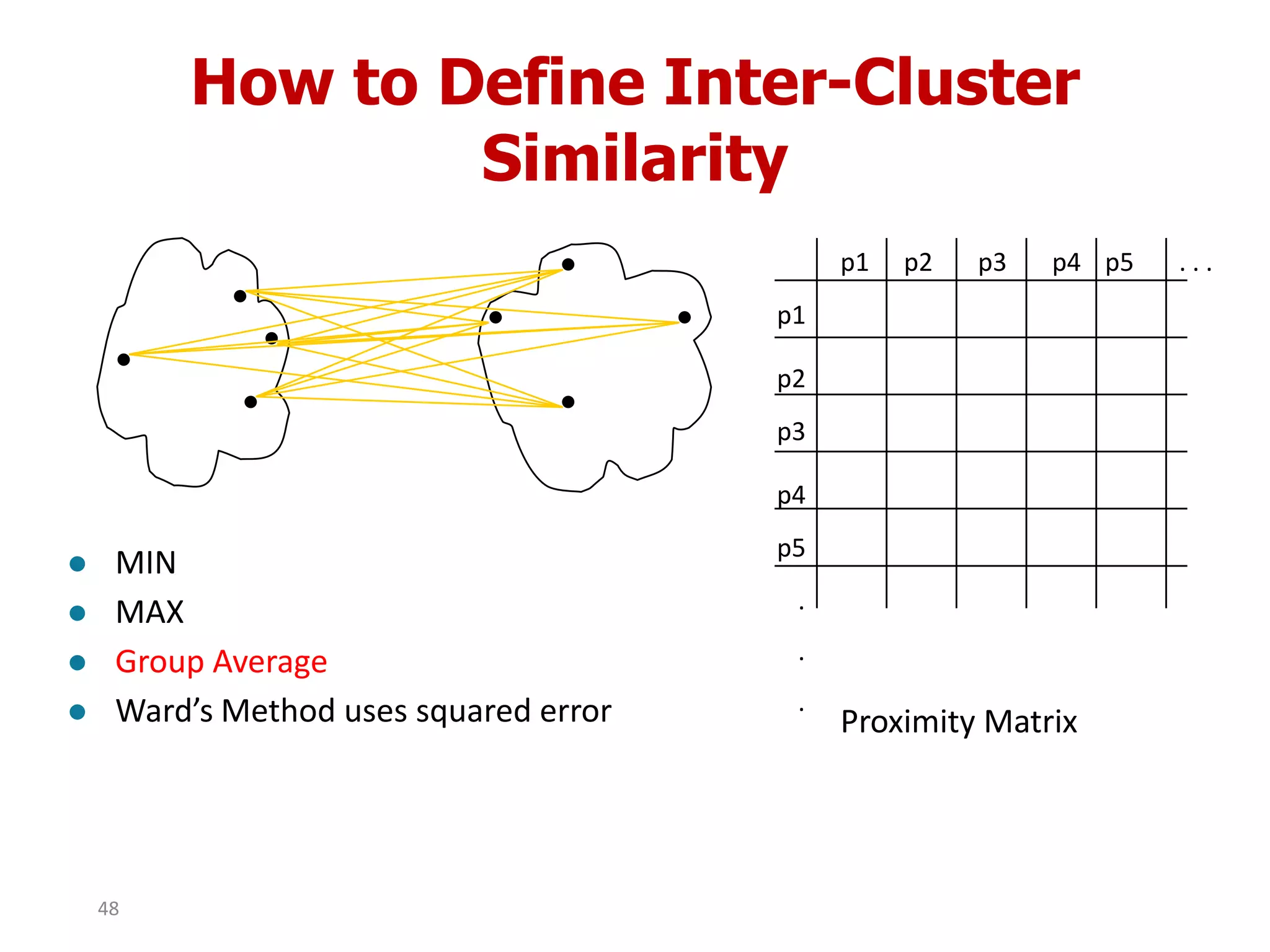
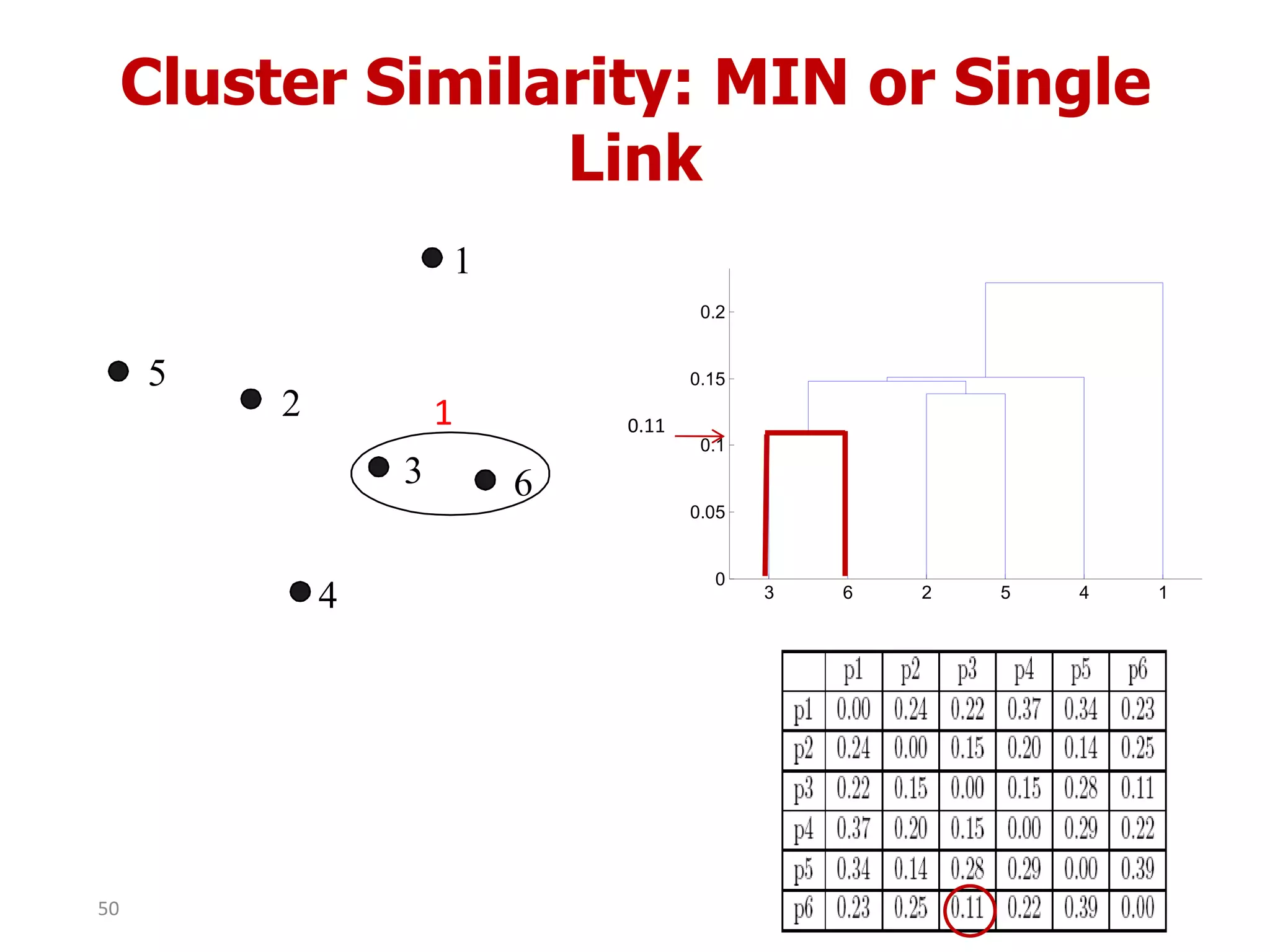
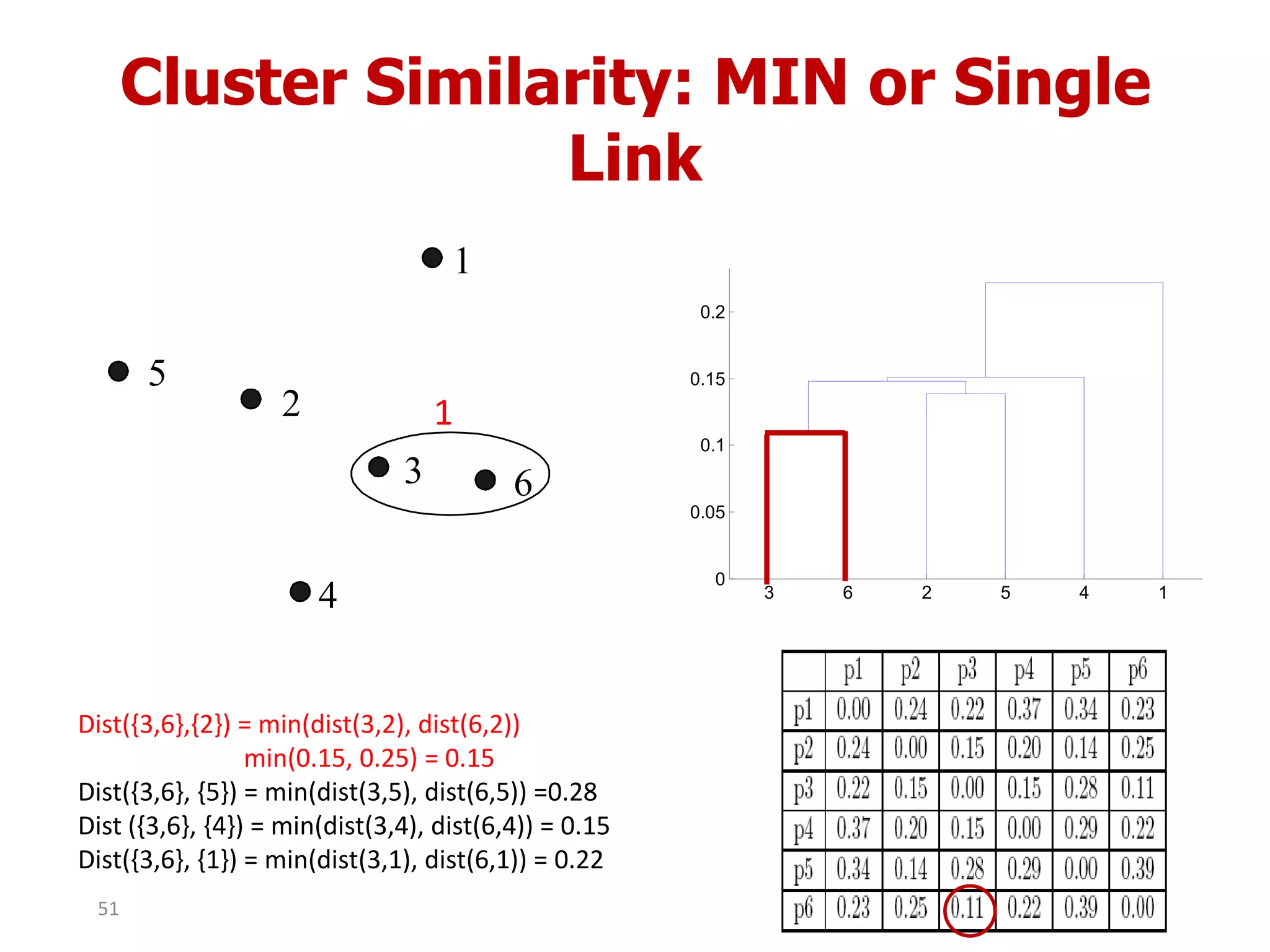
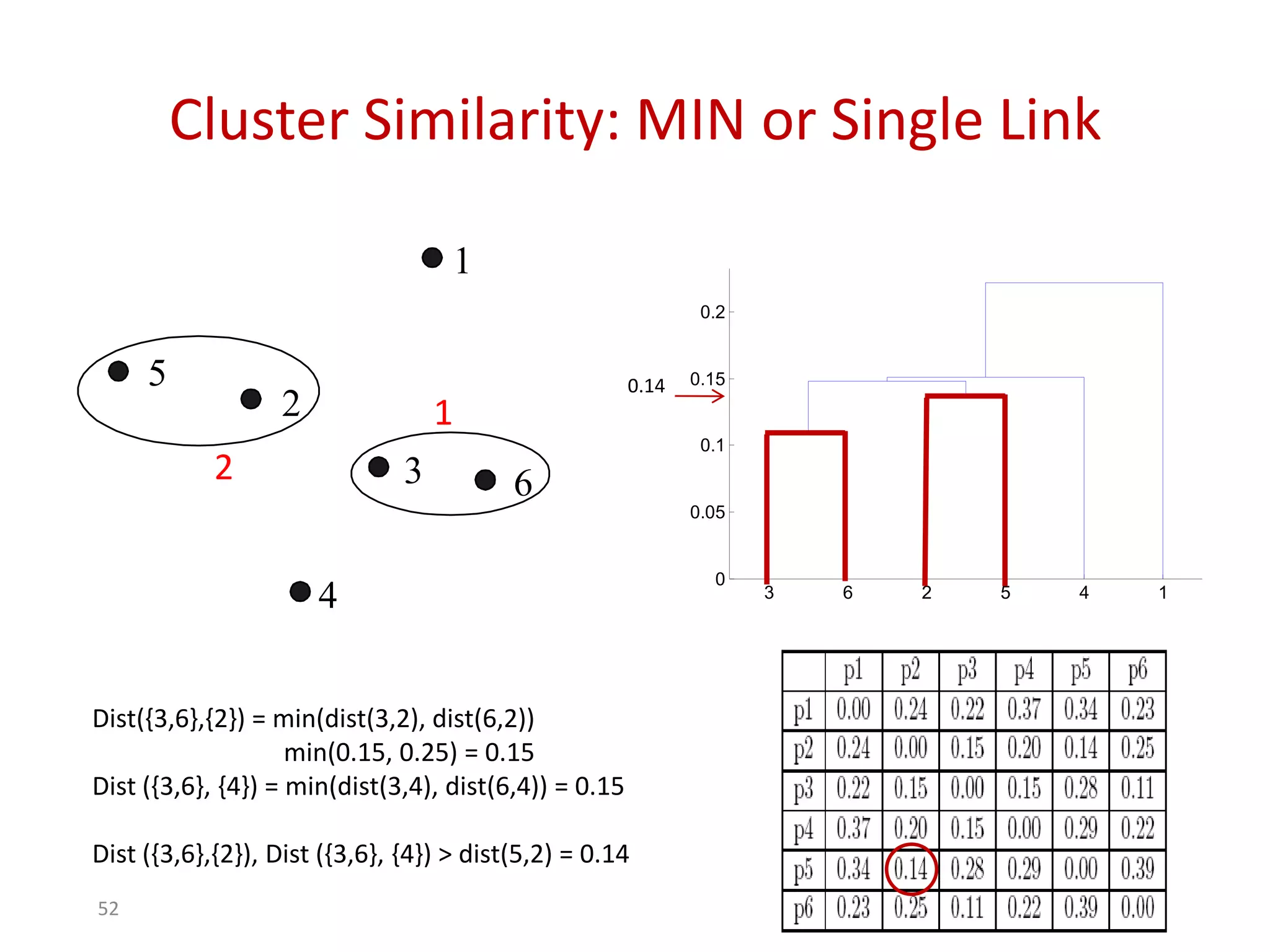
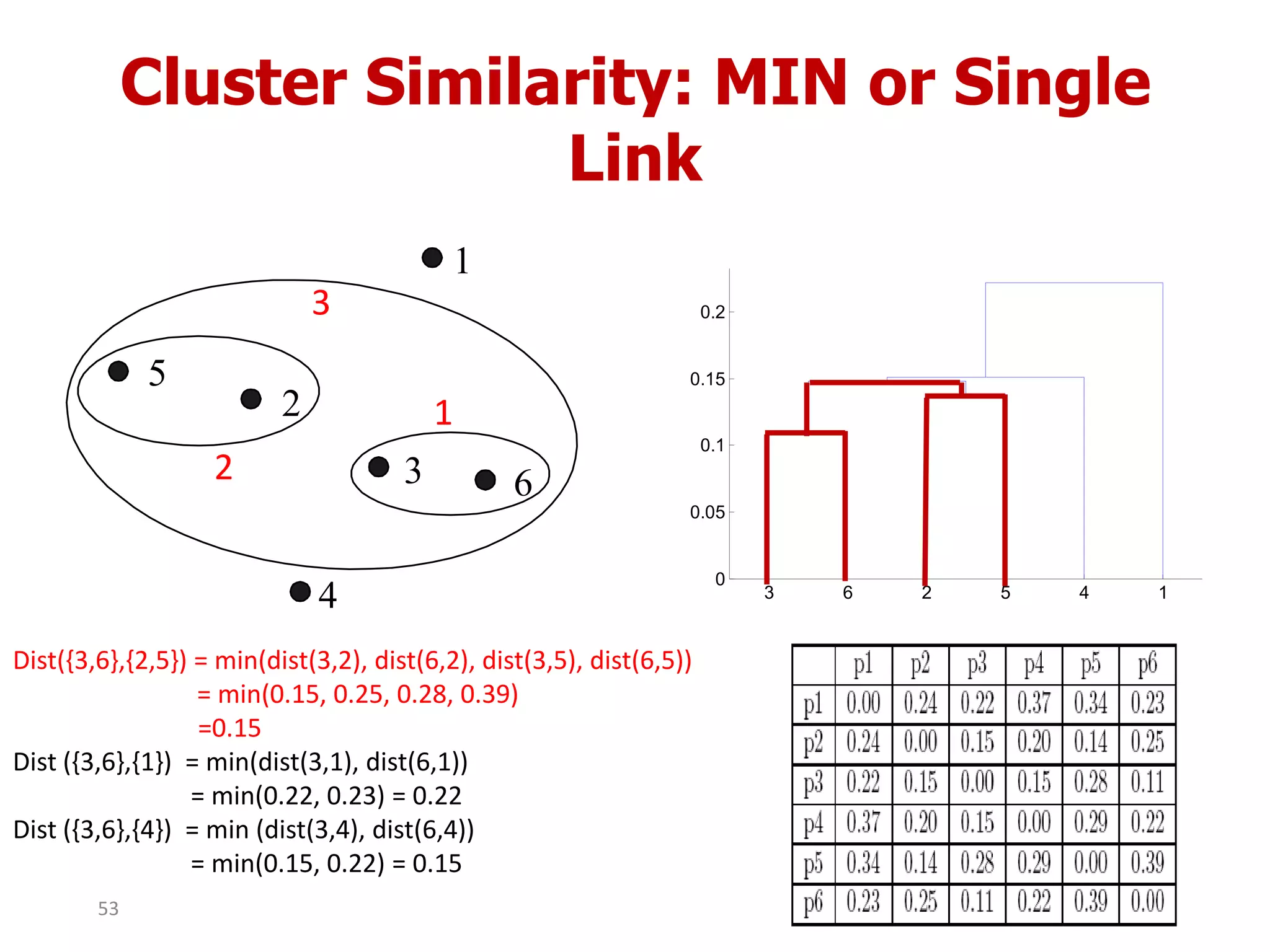
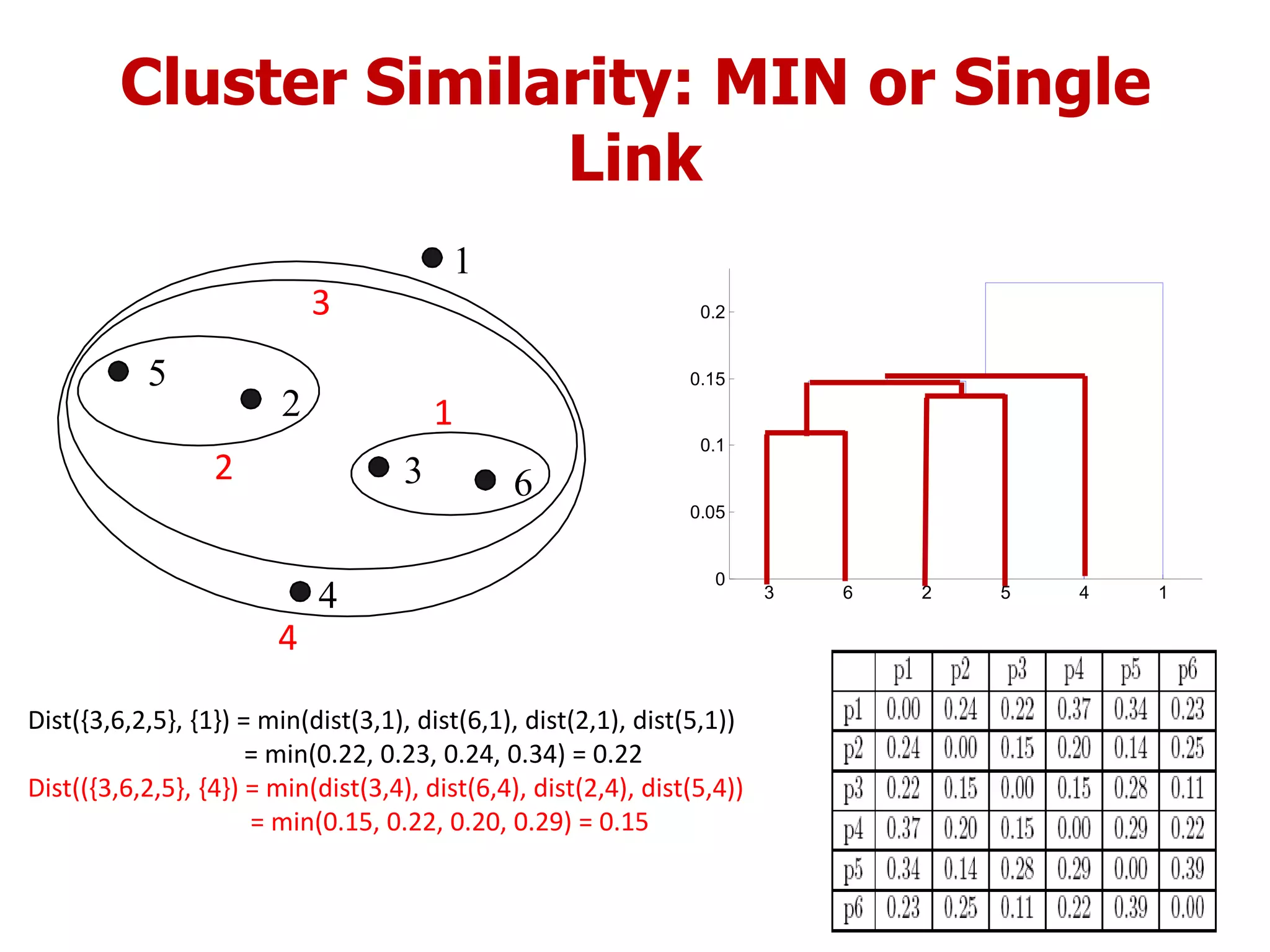
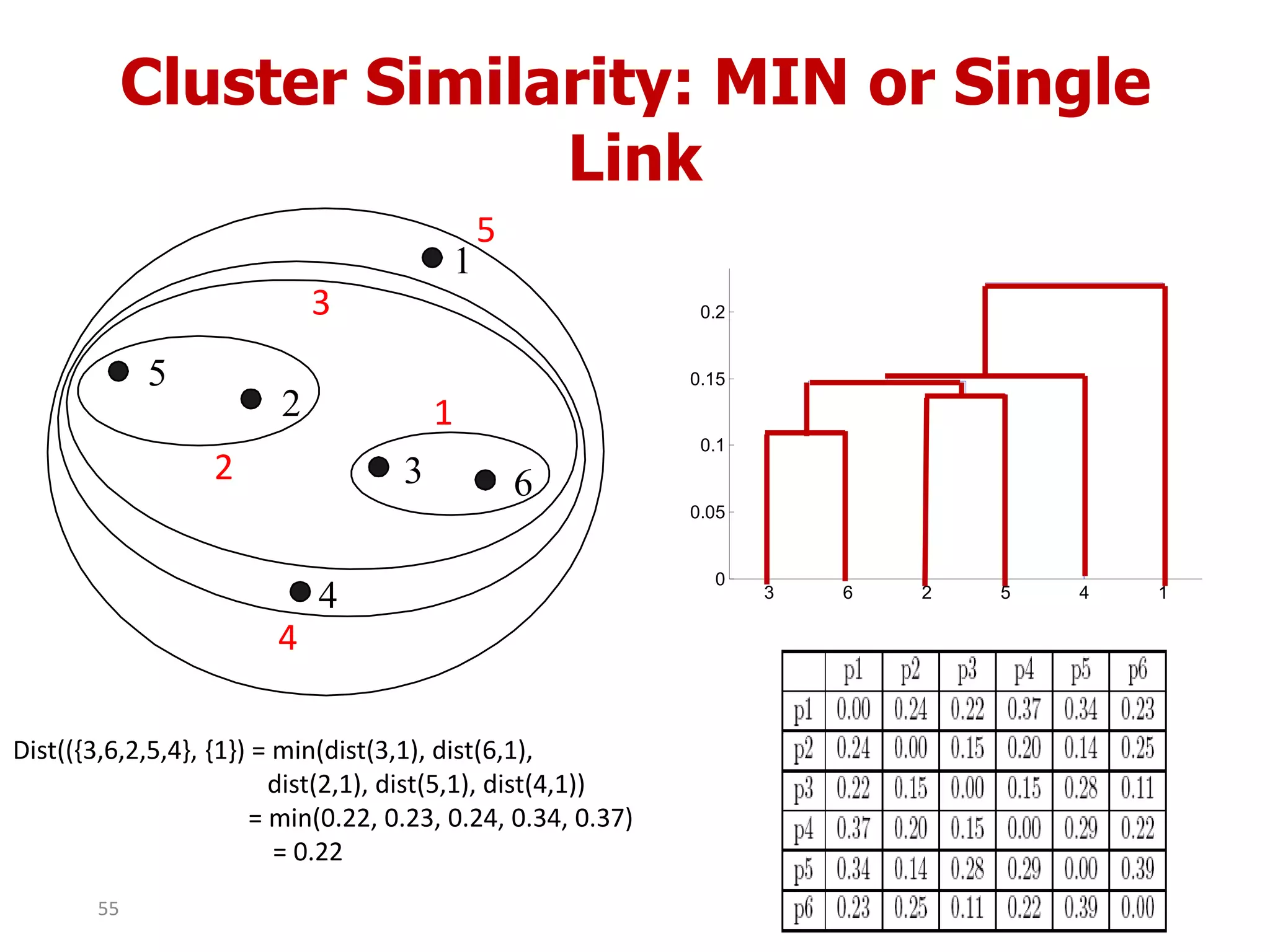
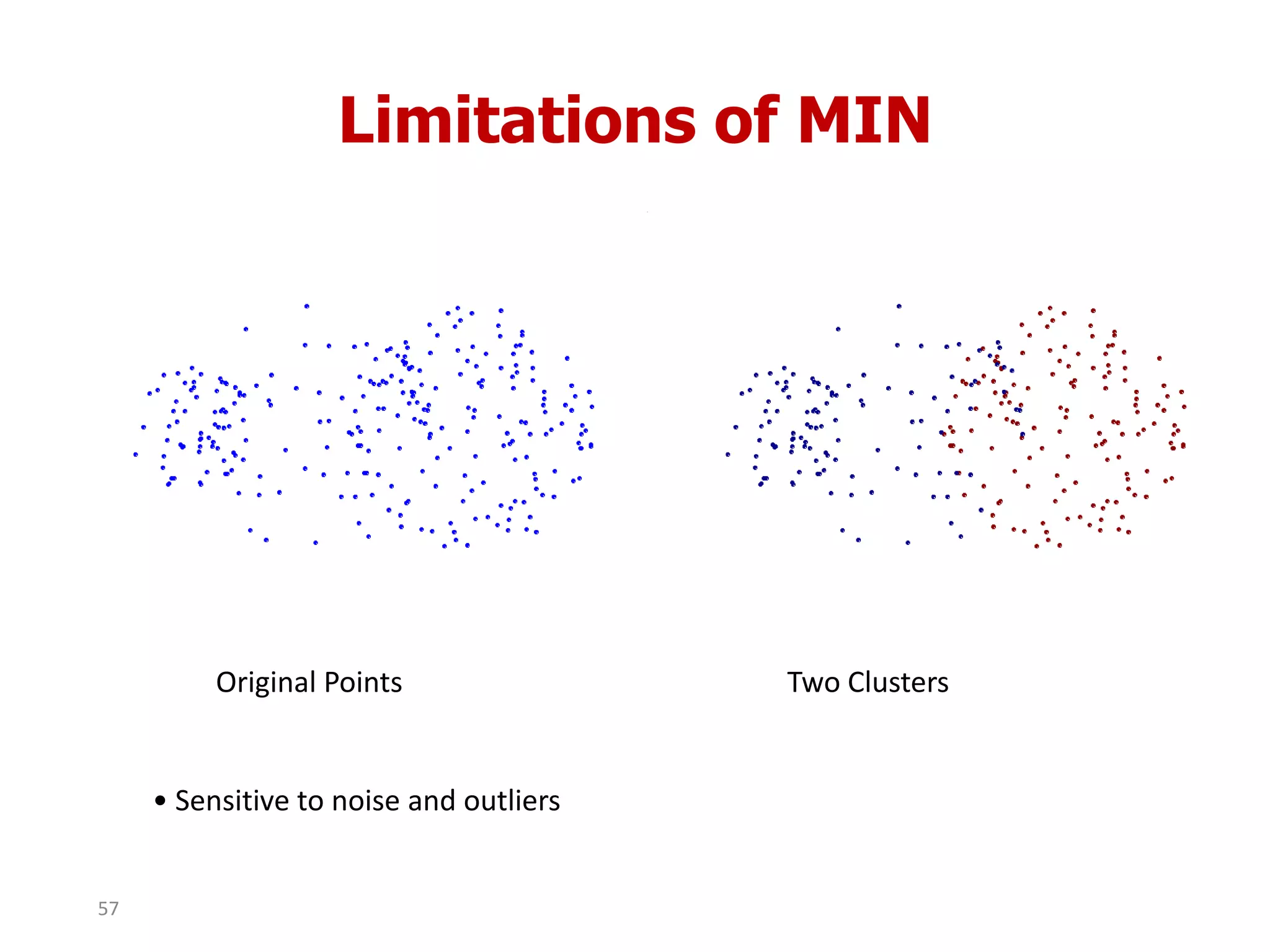
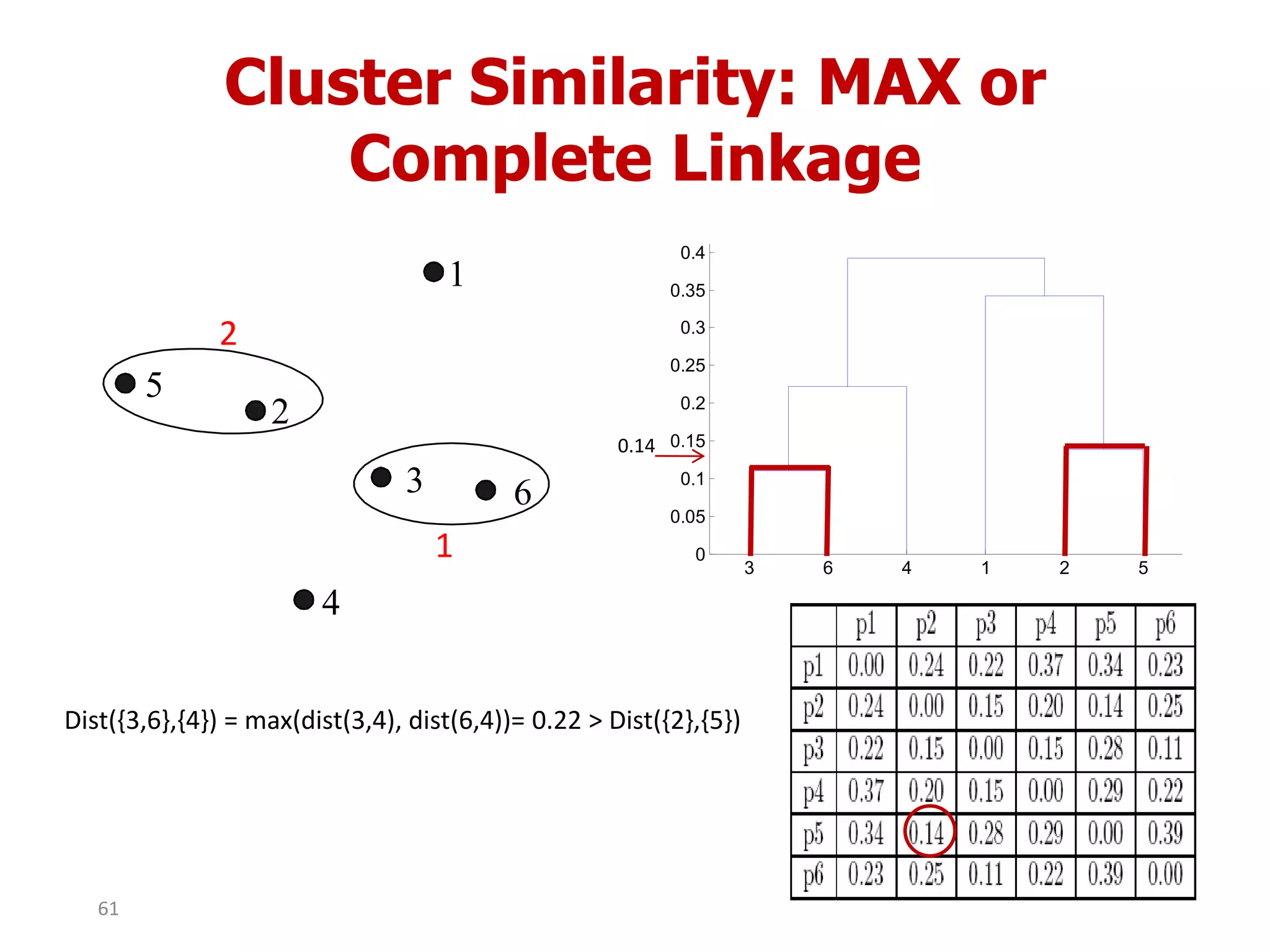
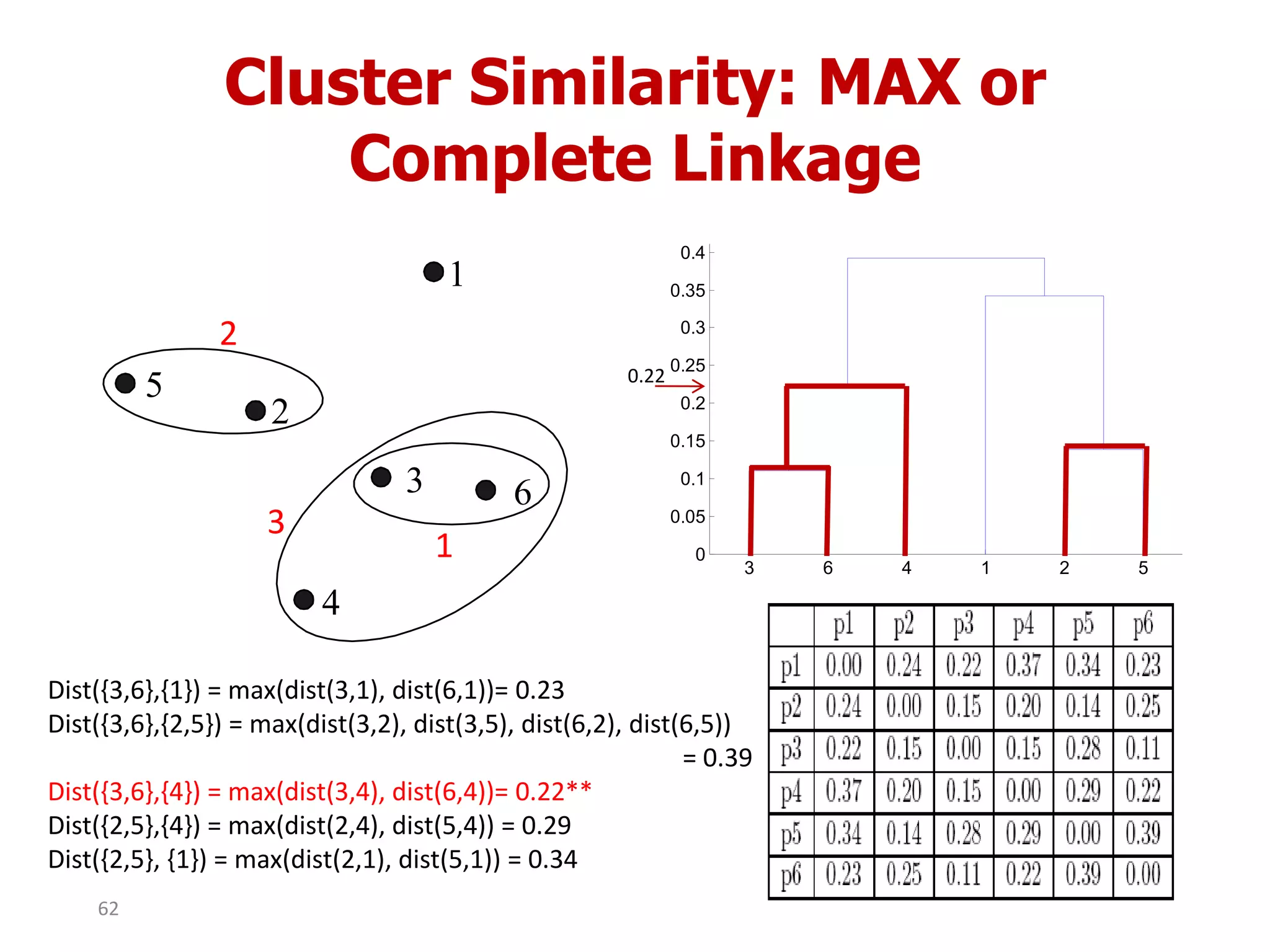
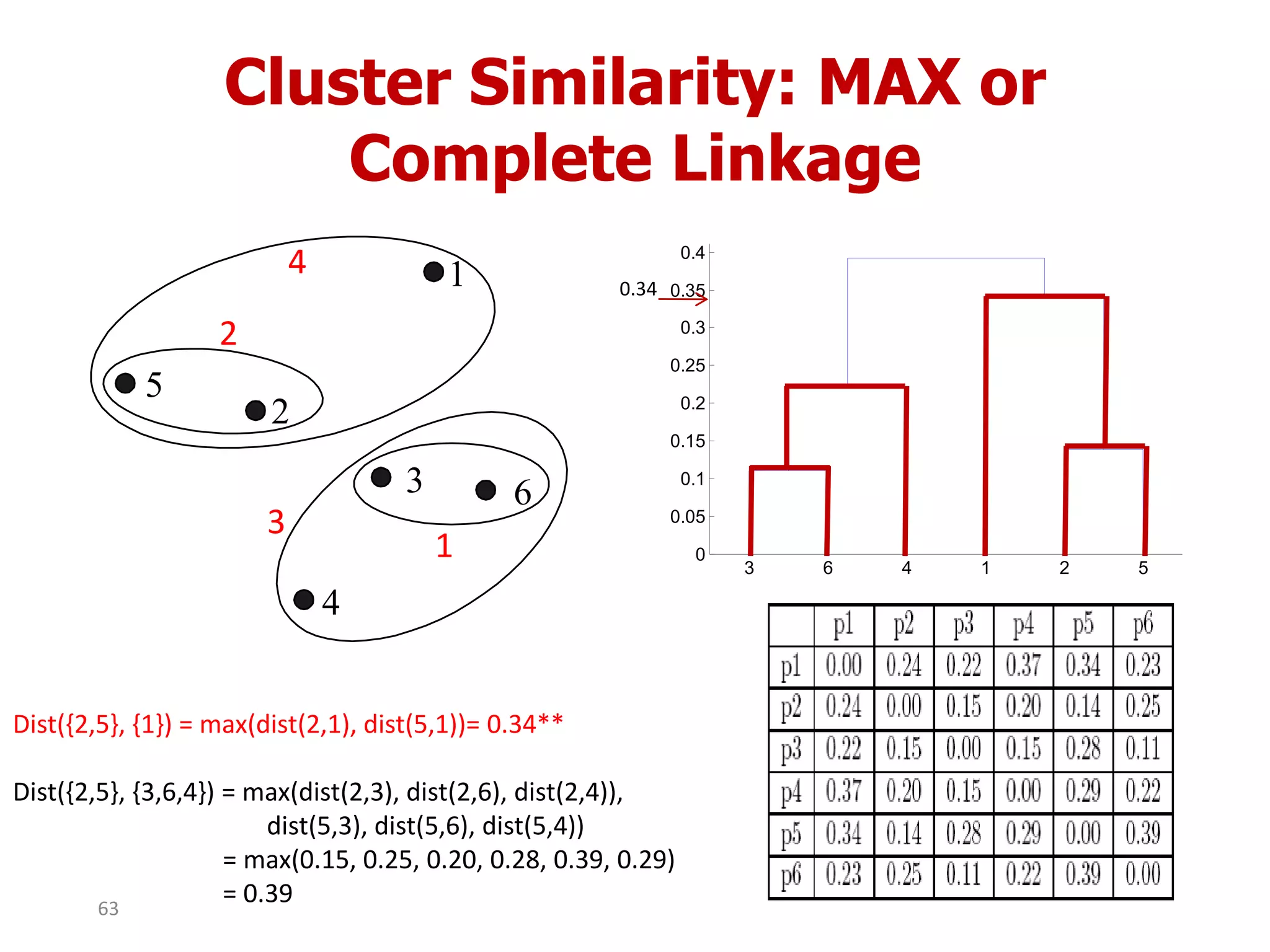
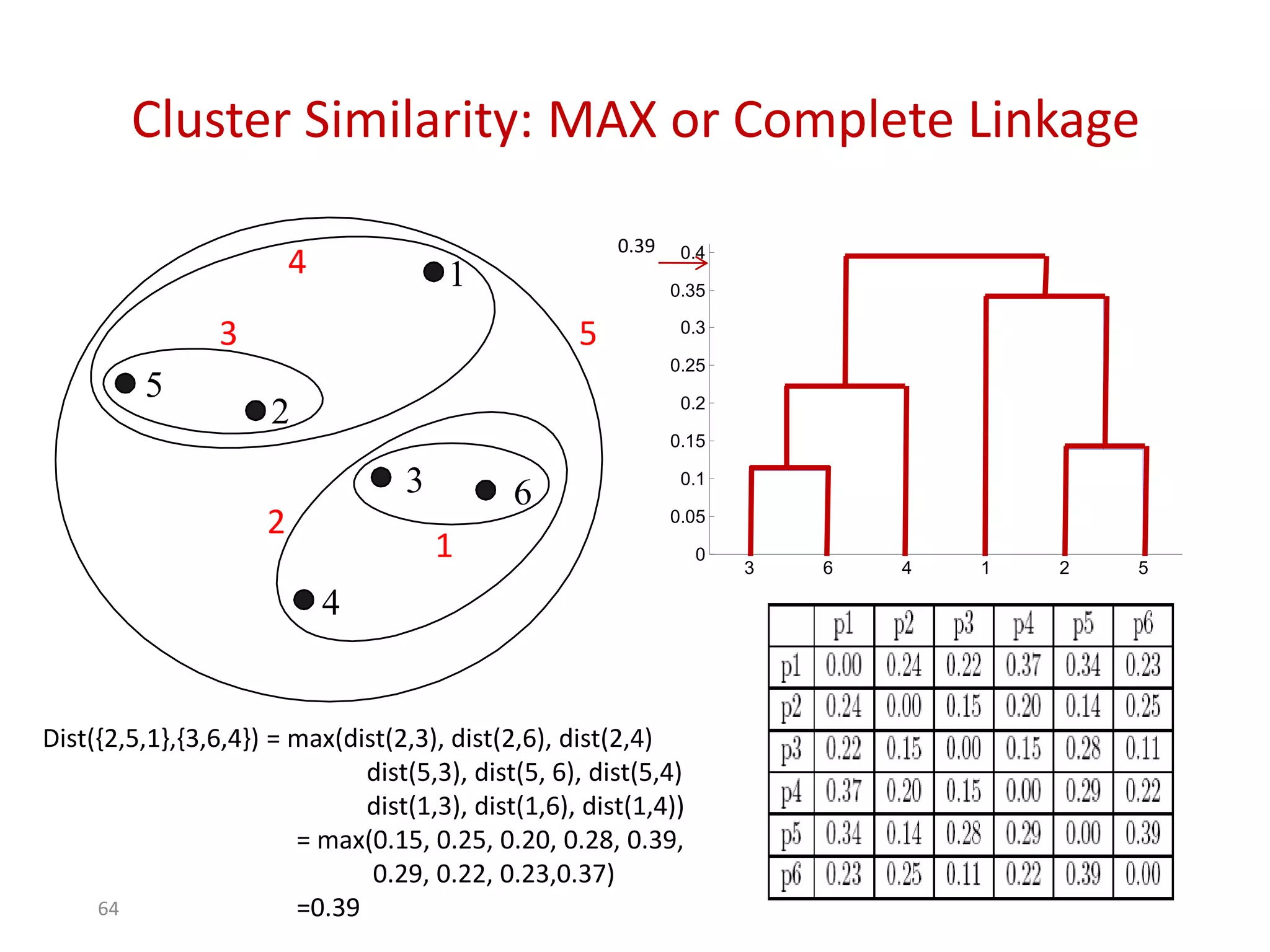
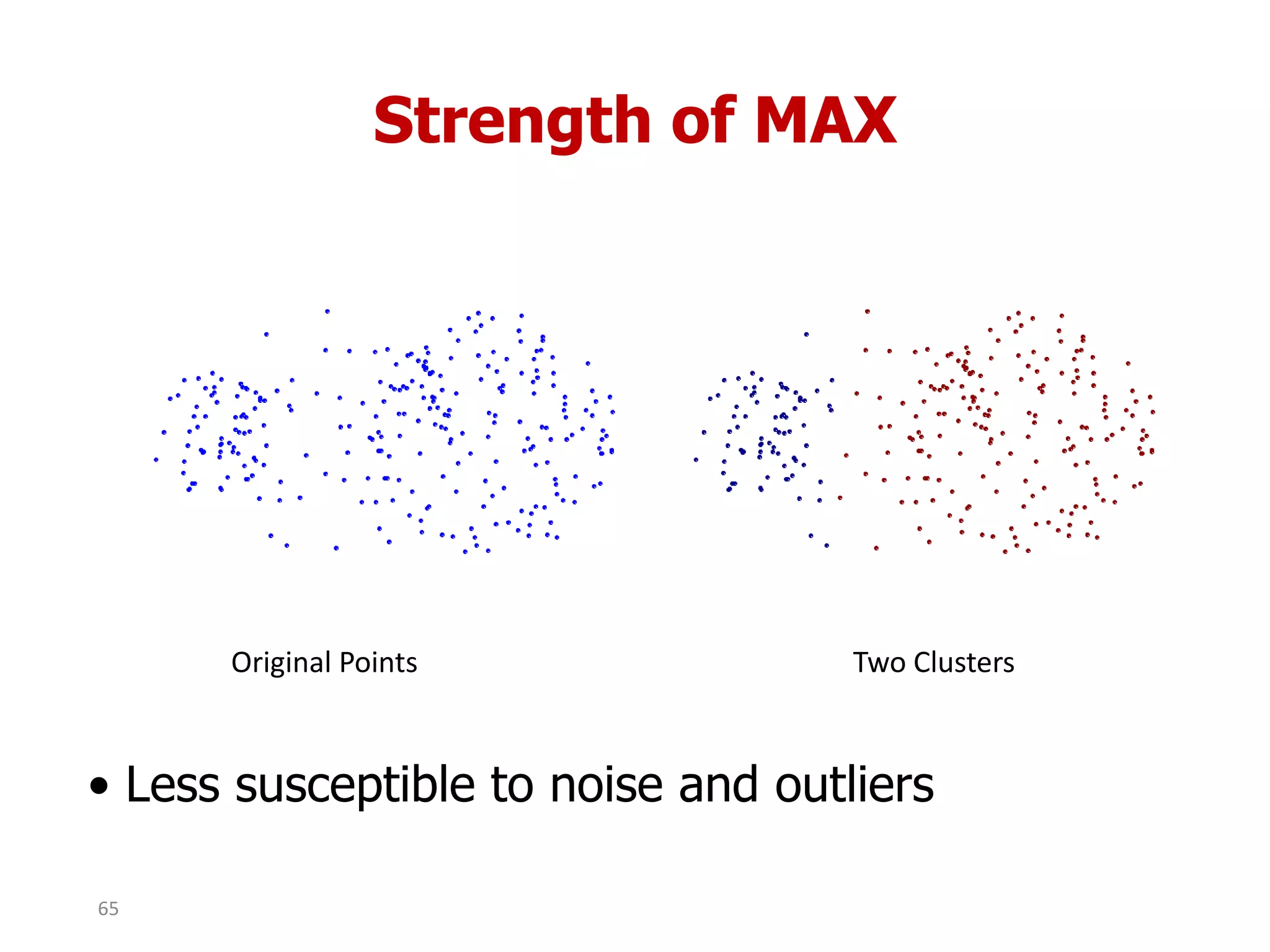
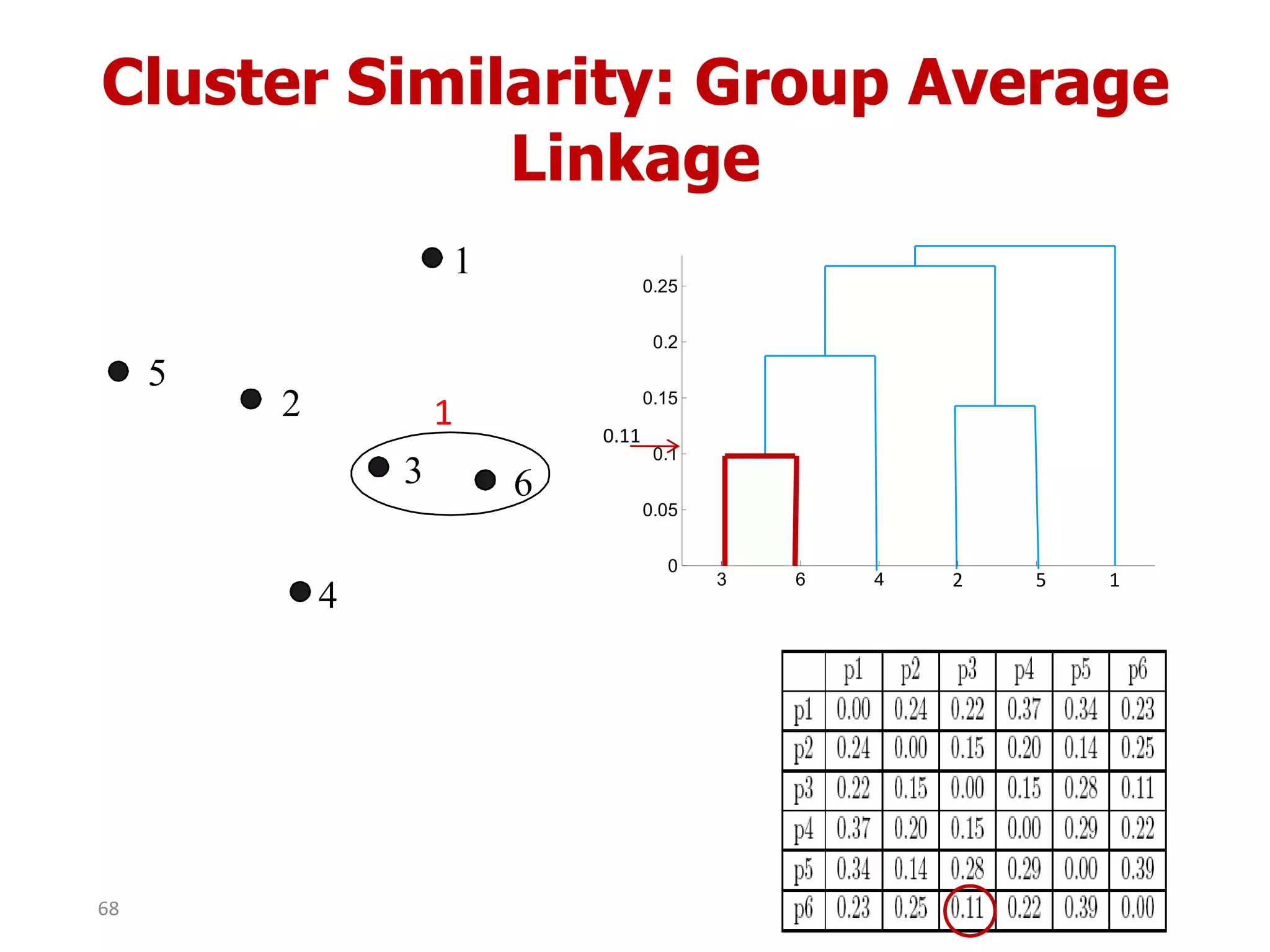
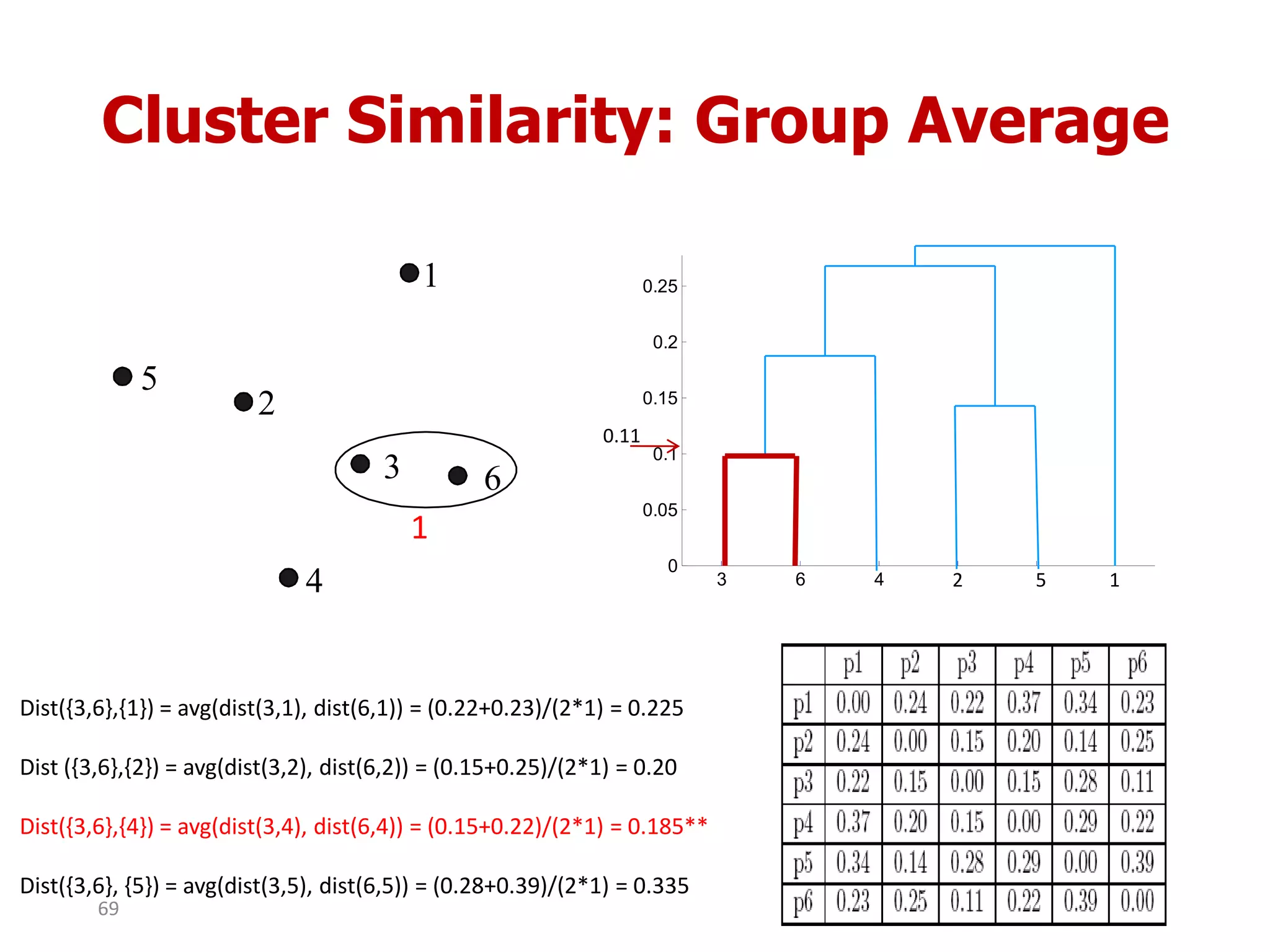
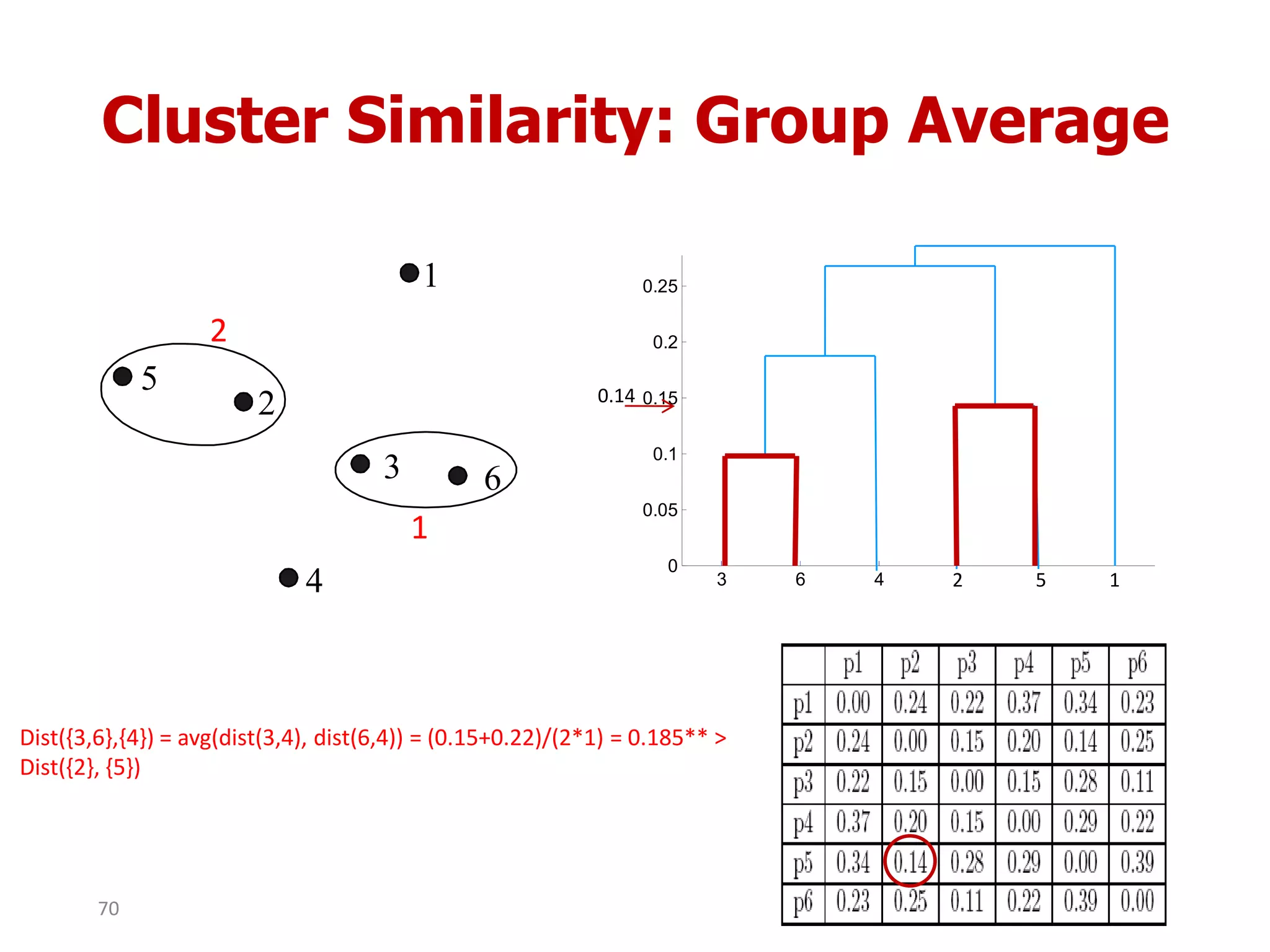
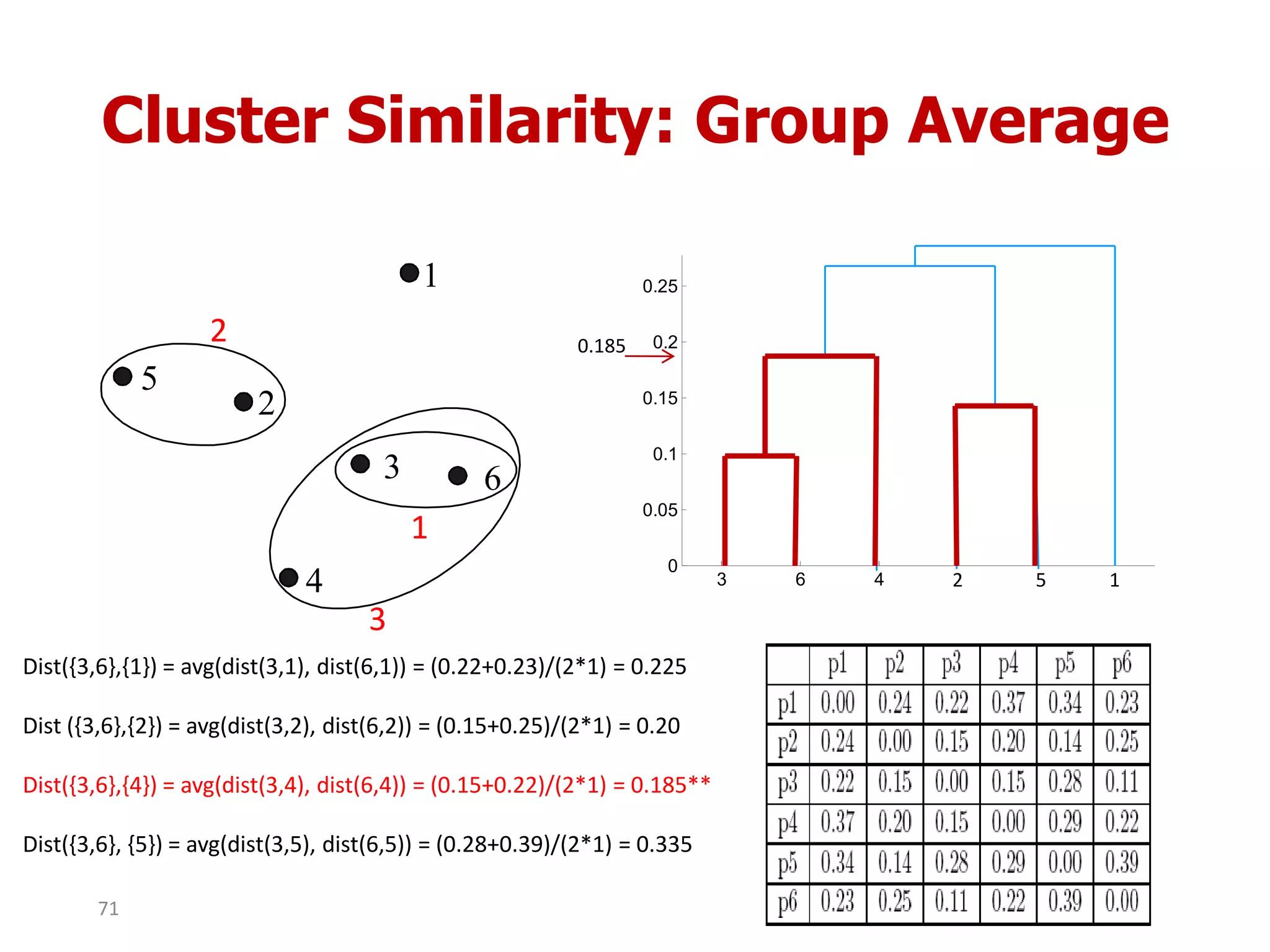
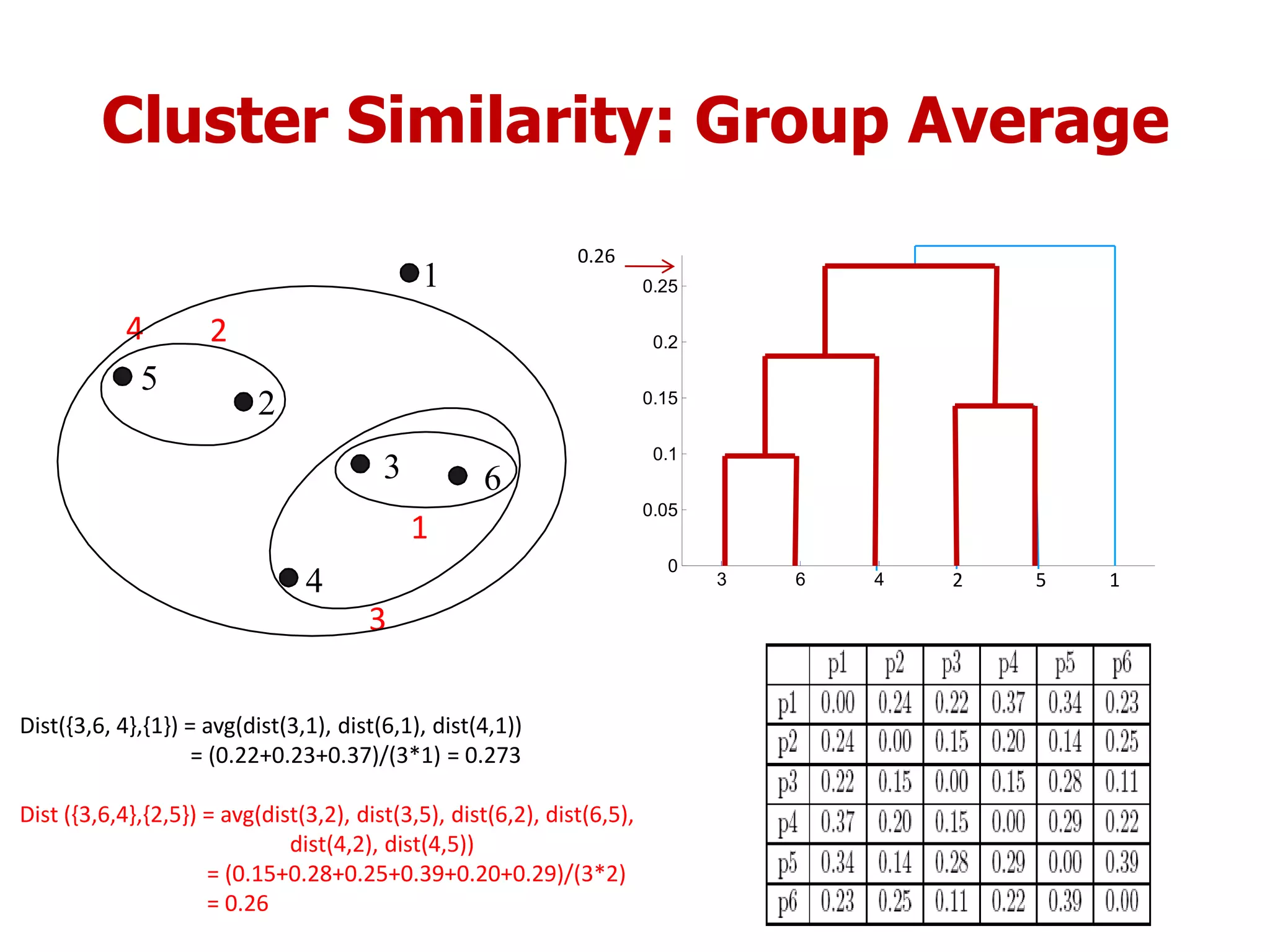
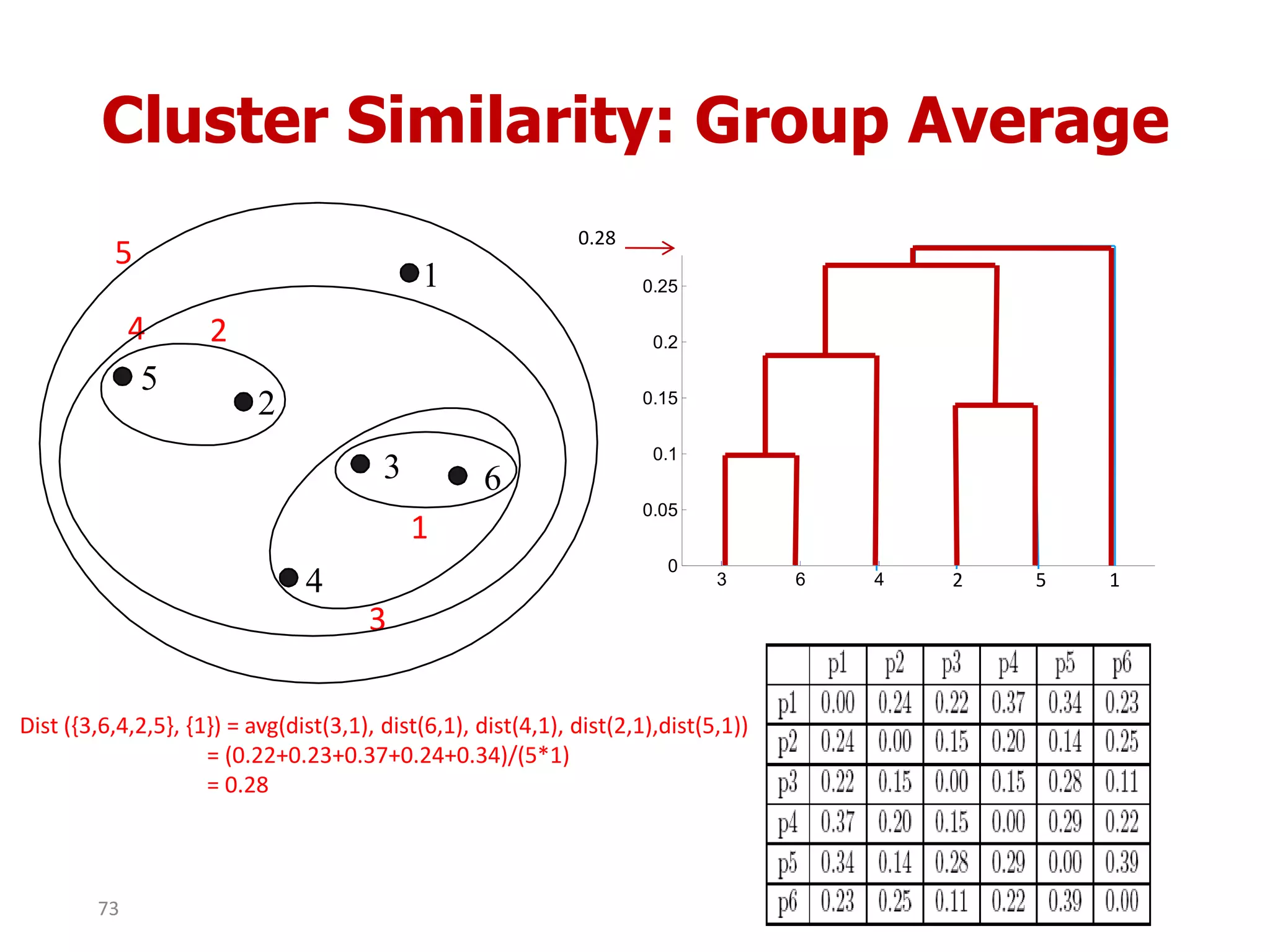
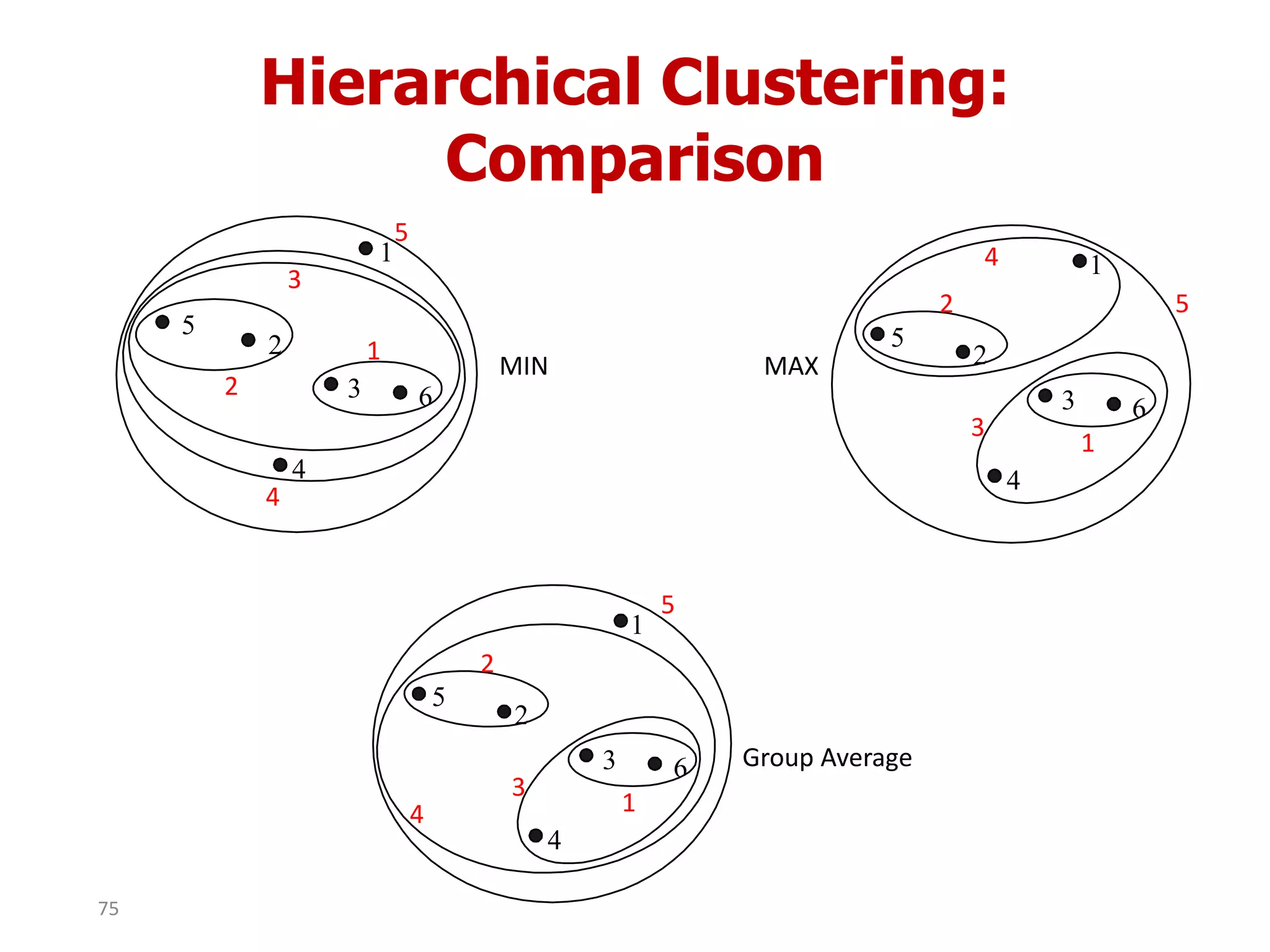
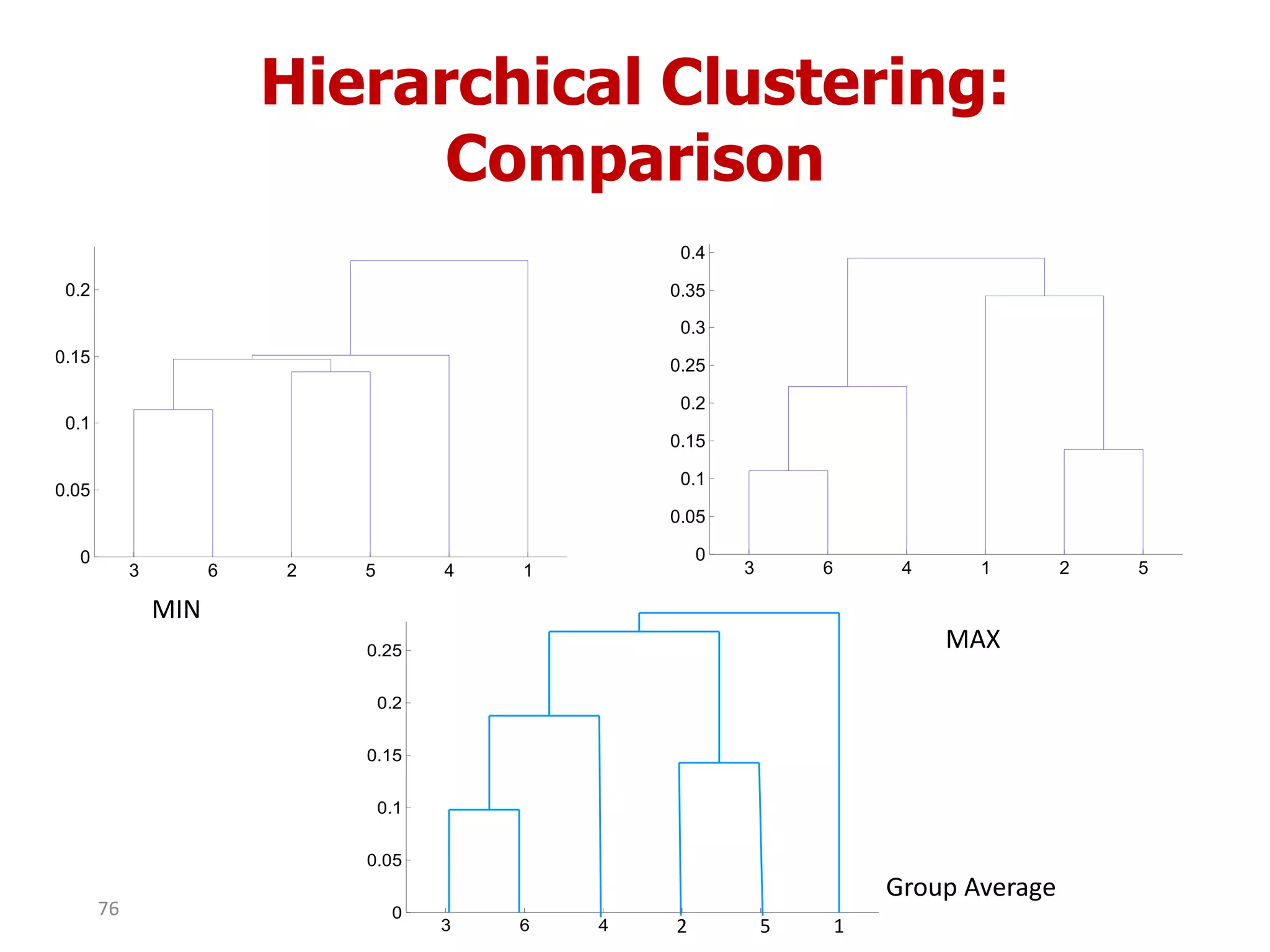
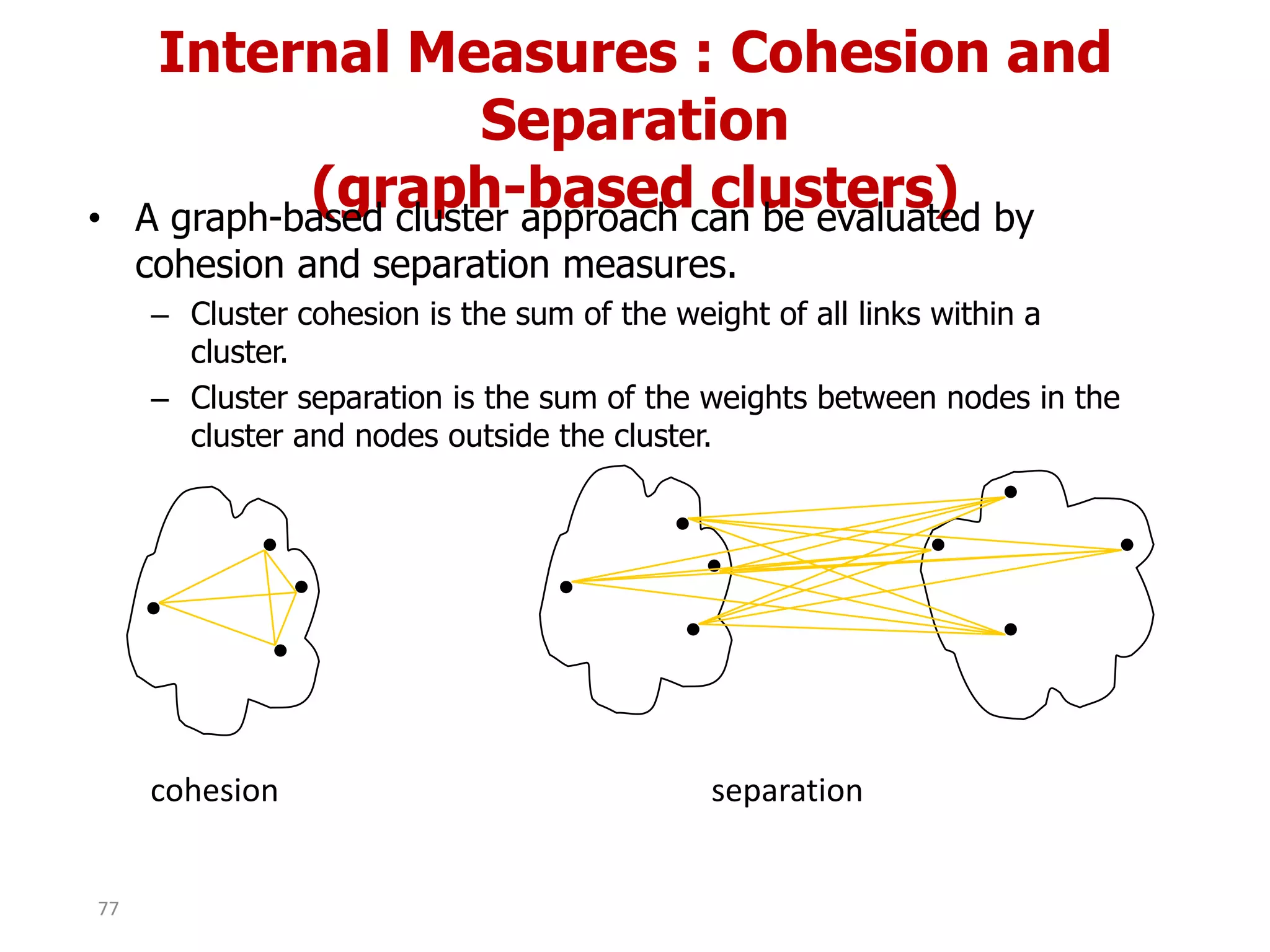
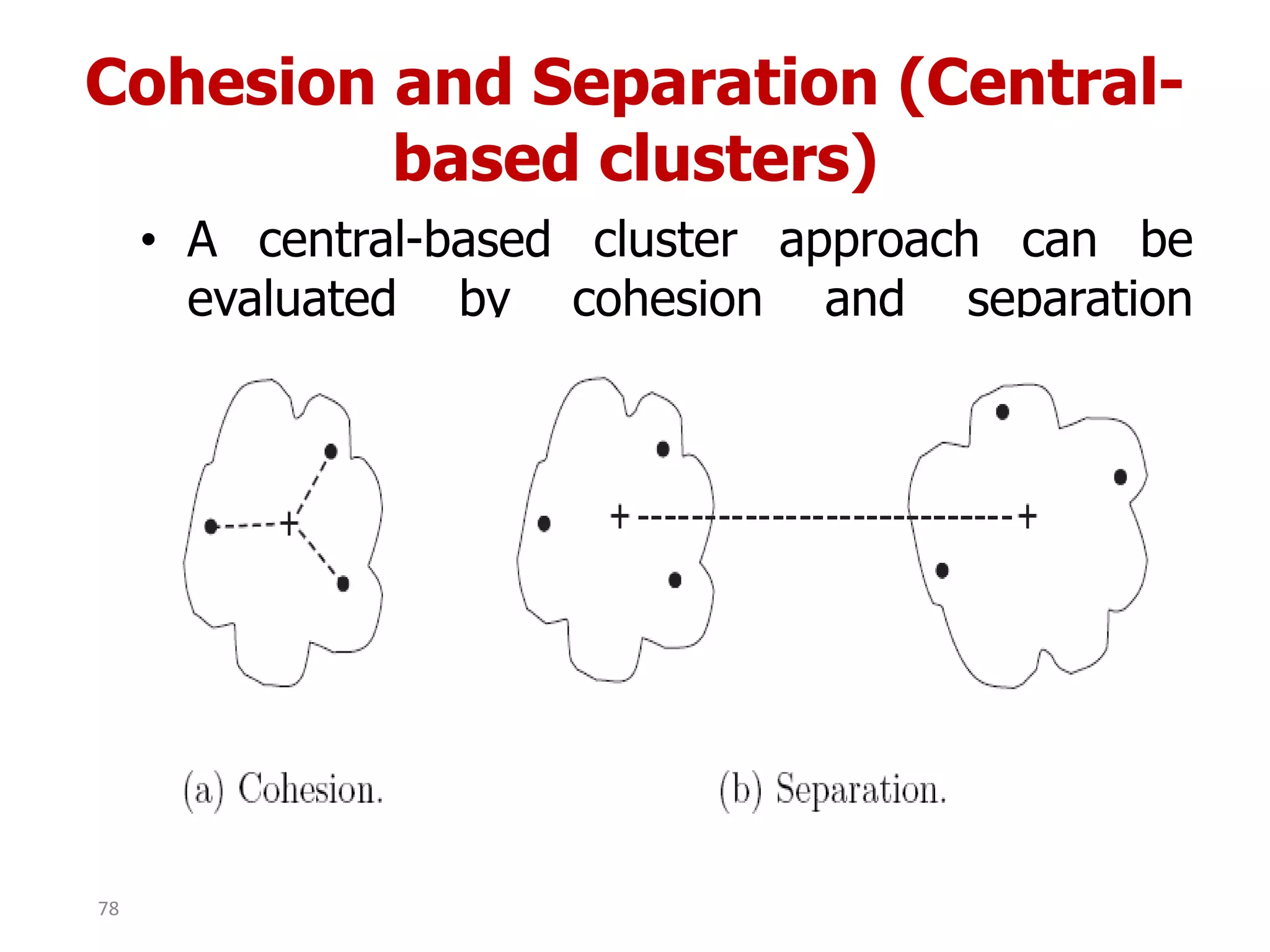
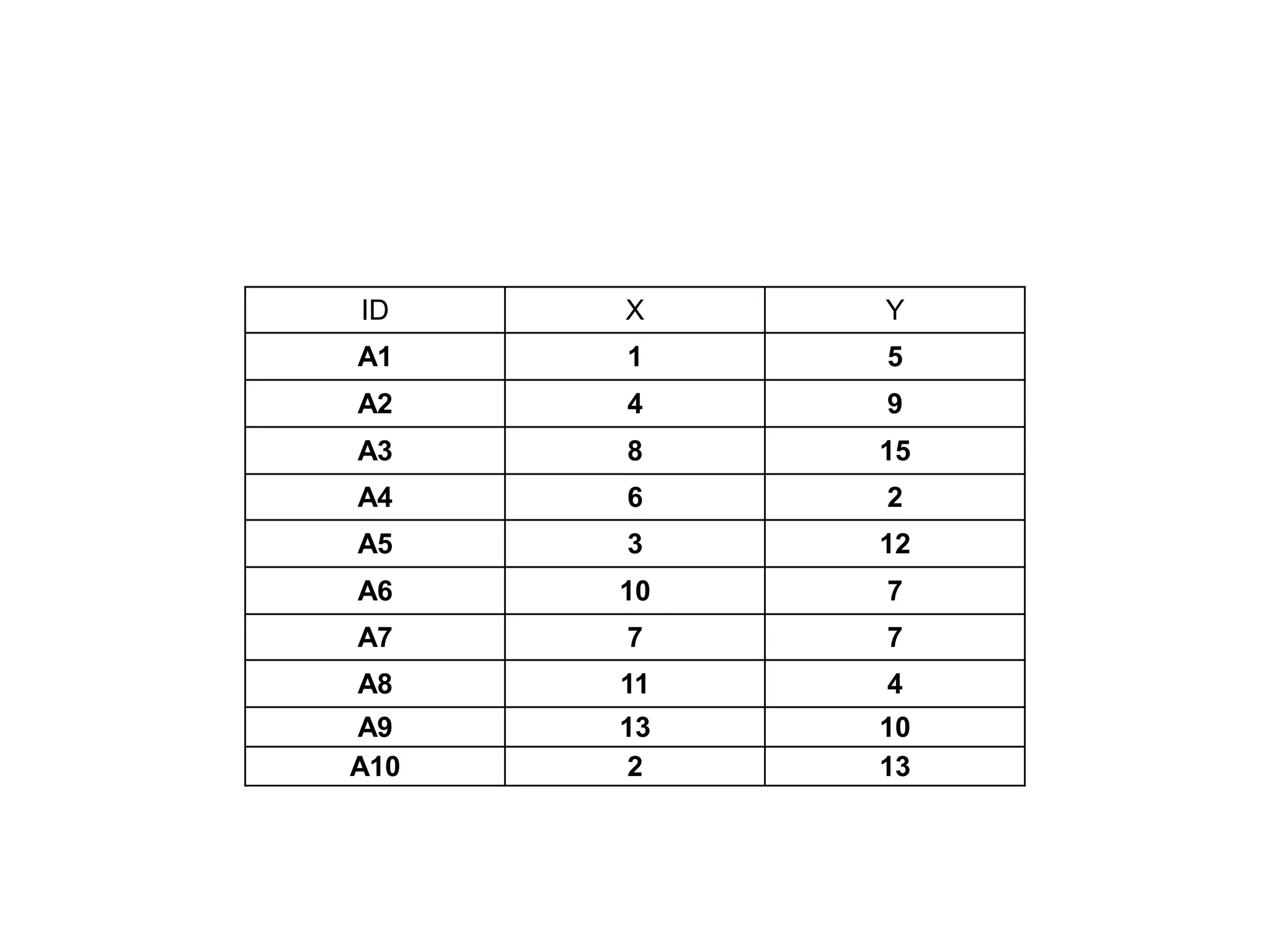
This document discusses different types of clustering analysis techniques in data mining. It describes clustering as the task of grouping similar objects together. The document outlines several key clustering algorithms including k-means clustering and hierarchical clustering. It provides an example to illustrate how k-means clustering works by randomly selecting initial cluster centers and iteratively assigning data points to clusters and recomputing cluster centers until convergence. The document also discusses limitations of k-means and how hierarchical clustering builds nested clusters through sequential merging of clusters based on a similarity measure.

1. .
:
(Clustering Analysis)
1

2. What is Clustering in Data Mining?
• Cluster : (collection)
– (Similarity)
– (Dissimilarity or
Distance)
• Cluster Analysis
–
• Clustering
– (Classification)
(unsupervised classification)
2

3. Cluster Analysis
How many clusters?
Four ClustersTwo Clusters
Six Clusters
3

4. What is Good Clustering?
•
(Minimize Intra-Cluster
Distances)
(Maximize Inter-Cluster Distances)
Inter-cluster
distances are
maximized
Intra-cluster
distances are
minimized
4

5. Types of Clustering
• Partitional Clustering
– A division data objects into non-overlapping subsets
(clusters) such that each data object is in exactly one subset
Original Points A Partitional Clustering
5

6. Types of Clustering
• Hierarchical clustering
– A set of nested clusters organized as a hierarchical tree
p4
p1
p3
p2
p4
p1
p3
p2
p4p1 p2 p3
p4p1 p2 p3
Hierarchical Clustering#1
Hierarchical Clustering#2 Traditional Dendrogram 2
Traditional Dendrogram 1
6

7. Types of Clustering
• Exclusive versus non-exclusive
– In non-exclusive clusterings, points may belong to multiple
clusters.
– Can represent multiple classes or „border‟ points
• Fuzzy versus non-fuzzy
– In fuzzy clustering, a point belongs to every cluster with
some weight between 0 and 1
– Weights must sum to 1
– Probabilistic clustering has similar characteristics
• Partial versus complete
– In some cases, we only want to cluster some of the data
• Heterogeneous versus homogeneous
– Cluster of widely different sizes, shapes, and densities
7

8. Characteristics of Cluster
• Well-Separated Clusters:
– A cluster is a set of points such that any point in a cluster is
closer (or more similar) to every other point in the cluster than
to any point not in the cluster.
3 well-separated clusters
8

9. Characteristics of Cluster
• Center-based
– A cluster is a set of objects such that an object in a cluster
is closer (more similar) to the “center” of a cluster, than to
the center of any other cluster.
– The center of a cluster is often a centroid, the average of all
the points in the cluster, or a medoid, the most
“representative” point of a cluster.
4 center-based clusters
9

10. Characteristics of Cluster
• Density-based
– A cluster is a dense region of points, which is separated by
low-density regions, from other regions of high density.
– Used when the clusters are irregular, and when noise and
outliers are present.
6 density-based clusters
10

11. Characteristics of Cluster
• Shared Property or Conceptual Clusters
– Finds clusters that share some common property
or represent a particular concept.
2 Overlapping Circles
11

12. Clustering Algorithms
• K-means clustering
• Hierarchical clustering
12

13. K-means Clustering
• (Partition) n
D k (
k)
• k-Means k
13

14. K-means Clustering Algorithm
Algorithm: The k-Means algorithm for partitioning based
on the mean value of object in the cluster.
Input: The number of cluster k and a database containing
n objects.
Output: A set of k clusters that mininimizes the squared-
error criterion.
14

15. K-means Clustering Algorithm
Method
1) Randomly choose k object as the initial cluster centers
(centroid);
2) Repeat
3) (re)assign each object to the cluster to which the object
is the most similar, based on the mean value of the
objects in the cluster;
4) Update the cluster mean
calculate the mean value of the objects for each
cluster;
5) Until centroid (center point) no change;
15

16. Example: K-Mean Clustering
• Problem: Cluster the following eight points (with (x,
y) representing locations) into three clusters A1(2,
10) A2(2, 5) A3(8, 4) A4(5, 8) A5(7, 5) A6(6, 4)
A7(1, 2) A8(4, 9).
0
2
4
6
8
10
12
0 1 2 3 4 5 6 7 8 9
16

17. Example: K-Mean Clustering
• Randomly choose k object as the initial cluster
centers;
• k =3 ; c1(2, 10), c2(5, 8) and c3(1, 2).
0
2
4
6
8
10
12
0 1 2 3 4 5 6 7 8 9
+
+
+
c1
c2
c3
17

18. Example: K-Mean Clustering
• The distance function between two points a=(x1, y1)
and b=(x2, y2) is defined as:
distance(a, b) = |x2 – x1| + |y2 – y1|
(2, 10) (5, 8) (1, 2)
Point Dist Mean 1 Dist Mean 2 Dist Mean 3 Cluster
A1 (2, 10)
A2 (2, 5)
A3 (8, 4)
A4 (5, 8)
A5 (7, 5)
A6 (6, 4)
A7 (1, 2)
A8 (4, 9)
18

19. Example: K-Mean Clustering
• Step 2 Calculate distance by using the
distance functionpoint mean1
x1, y1 x2, y2
(2, 10) (2, 10)
distance(point, mean1) = |x2 – x1| + |y2 – y1|
= |2 – 2| + |10 – 10|
= 0 + 0 = 0
point mean2
x1, y1 x2, y2
(2, 10) (5, 8)
distance(point, mean2) = |x2 – x1| + |y2 – y1|
= |5 – 2| + |8 – 10|
= 3 + 2 = 5
point mean3
x1, y1 x2, y2
(2, 10) (1, 2)
distance(point, mean3) = |x2 – x1| + |y2 – y1|
= |1 – 2| + |2 – 10|
= 1 + 8 = 9
19

20. Example: K-Mean Clustering
(2, 10) (5, 8) (1, 2)
Point Dist Mean 1 Dist Mean 2 Dist Mean 3 Cluster
A1 (2, 10) 0 5 9 1
A2 (2, 5)
A3 (8, 4)
A4 (5, 8)
A5 (7, 5)
A6 (6, 4)
A7 (1, 2)
A8 (4, 9)
20

21. Example: K-Mean Clustering
• Calculate distance by using the distance function
point mean1
x1, y1 x2, y2
(2, 5) (2, 10)
distance(point, mean1) = |x2 – x1| + |y2 – y1|
= |2 – 2| + |10 – 5|
= 0 + 5 = 5
point mean2
x1, y1 x2, y2
(2, 5) (5, 8)
distance(point, mean2) = |x2 – x1| + |y2 – y1|
= |5 – 2| + |8 – 5|
= 3 + 3 = 6
point mean3
x1, y1 x2, y2
(2, 5) (1, 2)
distance(point, mean3) = |x2 – x1| + |y2 – y1|
= |1 – 2| + |2 – 5|
= 1 + 3 = 4
21

22. Example: K-Mean Clustering
(2, 10) (5, 8) (1, 2)
Point Dist Mean 1 Dist Mean 2 Dist Mean 3 Cluster
A1 (2, 10) 0 5 9 1
A2 (2, 5) 5 6 4 3
A3 (8, 4)
A4 (5, 8)
A5 (7, 5)
A6 (6, 4)
A7 (1, 2)
A8 (4, 9)
22

23. Example: K-Mean Clustering
• Iteration#1
(2, 10) (5, 8) (1, 2)
Point Dist Mean 1 Dist Mean 2 Dist Mean 3 Cluster
A1 (2, 10) 0 5 9 1
A2 (2, 5) 5 6 4 3
A3 (8, 4) 12 7 9 2
A4 (5, 8) 5 0 10 2
A5 (7, 5) 10 5 9 2
A6 (6, 4) 10 5 7 2
A7 (1, 2) 9 10 0 3
A8 (4, 9) 3 2 10 2
23

24. Example: K-Mean Clustering
Cluster 1 Cluster 2 Cluster 3
A1(2, 10) A3(8, 4) A2(2, 5)
A4(5, 8) A7(1, 2)
A5(7, 5)
A6(6, 4)
A8(4, 9)
0
2
4
6
8
10
12
0 1 2 3 4 5 6 7 8 9
+
+
c1
c2
c3
+
24

25. Example: K-Mean Clustering
• re-compute the new cluster centers (means). We do
so, by taking the mean of all points in each cluster.
• For Cluster 1, we only have one point
A1(2, 10), which was the old mean, so the cluster
center remains the same.
• For Cluster 2, we have (
(8+5+7+6+4)/5, (4+8+5+4+9)/5 ) = (6, 6)
• For Cluster 3, we have ( (2+1)/2, (5+2)/2 ) =
(1.5, 3.5)
25

26. Example: K-Mean Clustering
0
2
4
6
8
10
12
0 1 2 3 4 5 6 7 8 9
+
+
c1
c2
c3
+
26

27. Example: K-Mean Clustering
• Iteration#2
(2, 10) (6, 6) (1.5, 3.5)
Point Dist Mean 1 Dist Mean 2 Dist Mean 3 Cluster
A1 (2, 10)
A2 (2, 5)
A3 (8, 4)
A4 (5, 8)
A5 (7, 5)
A6 (6, 4)
A7 (1, 2)
A8 (4, 9)
27

28. Example: K-Mean Clustering
(Iteration#2)
Cluster 1? Cluster 2? Cluster 3?
0
2
4
6
8
10
12
0 1 2 3 4 5 6 7 8 9
re-compute the new
cluster centers (means)
C1 = (2+4/2, 10+9/2)
= (3, 9.5)
C2 = (6.5, 5.25)
C3 = (1.5, 3.5)
28

29. Example: K-Mean Clustering
Iteration#3
Cluster 1? Cluster 2? Cluster 3?
0
2
4
6
8
10
12
0 1 2 3 4 5 6 7 8 9
re-compute the new
cluster centers (means)??
29

30. Distance functions
•
• Minkowski distance
• q=1 d Manhattan distance
• q=2 d Euclidean distance
q
q
jpip
q
ji
q
ji xxxxxxjid )...(),( 2211
jpipjiji xxxxxxjid ...),( 2211
)...(),(
22
22
2
11 jpipjiji xxxxxxjid
30

31. Evaluating K-means Clusters
• Most common measure is Sum of Squared
Error (SSE)
– For each point, the error is the distance to
the nearest cluster
– To get SSE, we square these errors and
sum them.
where,
– x is a data point in cluster Ci
– mi is the centroid point for cluster Ci
• can show that mi corresponds to the
K
i Cx
i
i
xmdistSSE
1
2
),(
31

32. Limitations of K-Mean
• K-means
–Size
–Density
–Shapes
32

33. Limitations of K-means: Differing
Sizes
• K-means
Original Points K-means (3 Clusters)
33

34. Limitations of K-means: Differing
Density
• K-means
Original Points K-means (3 Clusters)
34

35. Limitations of K-means: Non-
globular Shapes
• K-means
Original Points K-means (2 Clusters)
35

36. Overcoming K-means Limitations
Original Points K-means Clusters
One solution is to use many clusters.
Find parts of clusters, but need to put together.36

37. Overcoming K-means Limitations
Original Points K-means Clusters

38. Overcoming K-means Limitations
Original Points K-means Clusters
38

39. Hierarchical Clustering
•
Dendrogram
• Dendrogram
(cluster) (subcluster)
(cluster)
1 3 2 5 4 6
0
0.05
0.1
0.15
0.2
1
2
3
4
5
6
1
2
3 4
5
Dendrogram
39

40. Hierarchical Clustering
2
1. Agglomerative ( ) :
Agglomerative
2. Divisive ( ) :
Divisive Agglomerative
(singleton
cluster) cluster
40

41. Agglomerative Clustering Algorithm
Basic algorithm is straightforward
1. Compute the proximity matrix
2. Let each data point be a cluster
3. Repeat
4. Merge the two closest clusters
5. Update the proximity matrix
6. Until only a single cluster remains
41

42. Example:
42

43. Example:
43

44. Example:
6
Euclidean distance
44

45. How to Define Inter-Cluster
Similarity
p1
p3
p5
p4
p2
p1 p2 p3 p4 p5 . . .
.
.
.
Similarity?
Proximity Matrix
 MIN
 MAX
 Group Average
 Ward’s Method uses squared
error
45

46. How to Define Inter-Cluster
Similarity
 MIN
 MAX
 Group Average
 Ward’s Method uses squared
error
p1
p3
p5
p4
p2
p1 p2 p3 p4 p5 . . .
.
.
.
Proximity Matrix
46

47. How to Define Inter-Cluster Similarity
p1
p3
p5
p4
p2
p1 p2 p3 p4 p5 . . .
.
.
.
Proximity Matrix
 MIN
 MAX
 Group Average
 Ward’s Method uses squared error
47

48. How to Define Inter-Cluster
Similarity
p1
p3
p5
p4
p2
p1 p2 p3 p4 p5 . . .
.
.
.
Proximity Matrix
 MIN
 MAX
 Group Average
 Ward’s Method uses squared error
48

49. Cluster Similarity: MIN or Single
Link
• Single link MIN
Hierarchical Clustering
2
49

50. Cluster Similarity: MIN or Single
Link
1
2
3
4
5
6
1
3 6 2 5 4 1
0
0.05
0.1
0.15
0.2
0.11
50

51. Cluster Similarity: MIN or Single
Link
1
2
3
4
5
6
1
3 6 2 5 4 1
0
0.05
0.1
0.15
0.2
Dist({3,6},{2}) = min(dist(3,2), dist(6,2))
min(0.15, 0.25) = 0.15
Dist({3,6}, {5}) = min(dist(3,5), dist(6,5)) =0.28
Dist ({3,6}, {4}) = min(dist(3,4), dist(6,4)) = 0.15
Dist({3,6}, {1}) = min(dist(3,1), dist(6,1)) = 0.22
51

52. Cluster Similarity: MIN or Single Link
1
2
3
4
5
6
1
2
3 6 2 5 4 1
0
0.05
0.1
0.15
0.2
Dist({3,6},{2}) = min(dist(3,2), dist(6,2))
min(0.15, 0.25) = 0.15
Dist ({3,6}, {4}) = min(dist(3,4), dist(6,4)) = 0.15
Dist ({3,6},{2}), Dist ({3,6}, {4}) > dist(5,2) = 0.14
0.14
52

53. Cluster Similarity: MIN or Single
Link
1
2
3
4
5
6
1
2
3
3 6 2 5 4 1
0
0.05
0.1
0.15
0.2
Dist({3,6},{2,5}) = min(dist(3,2), dist(6,2), dist(3,5), dist(6,5))
= min(0.15, 0.25, 0.28, 0.39)
=0.15
Dist ({3,6},{1}) = min(dist(3,1), dist(6,1))
= min(0.22, 0.23) = 0.22
Dist ({3,6},{4}) = min (dist(3,4), dist(6,4))
= min(0.15, 0.22) = 0.15
53

54. Cluster Similarity: MIN or Single
Link
1
2
3
4
5
6
1
2
3
4
3 6 2 5 4 1
0
0.05
0.1
0.15
0.2
Dist({3,6,2,5}, {1}) = min(dist(3,1), dist(6,1), dist(2,1), dist(5,1))
= min(0.22, 0.23, 0.24, 0.34) = 0.22
Dist(({3,6,2,5}, {4}) = min(dist(3,4), dist(6,4), dist(2,4), dist(5,4))
= min(0.15, 0.22, 0.20, 0.29) = 0.15

55. Cluster Similarity: MIN or Single
Link
1
2
3
4
5
6
1
2
3
4
5
3 6 2 5 4 1
0
0.05
0.1
0.15
0.2
Dist(({3,6,2,5,4}, {1}) = min(dist(3,1), dist(6,1),
dist(2,1), dist(5,1), dist(4,1))
= min(0.22, 0.23, 0.24, 0.34, 0.37)
= 0.22
55

56. Strength of MIN
Original Points Two Clusters
• Can handle non-elliptical shapes
56

57. Limitations of MIN
•
Original Points Two Clusters
• Sensitive to noise and outliers
57

58. Cluster Similarity: MAX or
Complete Linkage
• Complete link MAX
Hierarchical Clustering
2
58

59. 3 6 4 1 2 5
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Cluster Similarity: MAX or
Complete Linkage
1
2
3
4
5
6
1
0.11
59

60. Cluster Similarity: MAX or
Complete Linkage
3 6 4 1 2 5
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
1
2
3
4
5
6
1
Dist({3,6},{1}) = max(dist(3,1), dist(6,1))= 0.23
Dist({3,6},{2}) = max(dist(3,2), dist(6,2))= 0.25
Dist({3,6},{4}) = max(dist(3,4), dist(6,4))= 0.22**
Dist({3,6},{5}) = max(dist(3,5), dist(6,5))= 0.3960

61. Cluster Similarity: MAX or
Complete Linkage
3 6 4 1 2 5
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
1
2
3
4
5
6
1
2
Dist({3,6},{4}) = max(dist(3,4), dist(6,4))= 0.22 > Dist({2},{5})
0.14
61

62. Cluster Similarity: MAX or
Complete Linkage
3 6 4 1 2 5
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
1
2
3
4
5
6
1
3
Dist({3,6},{1}) = max(dist(3,1), dist(6,1))= 0.23
Dist({3,6},{2,5}) = max(dist(3,2), dist(3,5), dist(6,2), dist(6,5))
= 0.39
Dist({3,6},{4}) = max(dist(3,4), dist(6,4))= 0.22**
Dist({2,5},{4}) = max(dist(2,4), dist(5,4)) = 0.29
Dist({2,5}, {1}) = max(dist(2,1), dist(5,1)) = 0.34
0.22
2
62

63. Cluster Similarity: MAX or
Complete Linkage
3 6 4 1 2 5
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
1
2
3
4
5
6
1
2
3
4
Dist({2,5}, {1}) = max(dist(2,1), dist(5,1))= 0.34**
Dist({2,5}, {3,6,4}) = max(dist(2,3), dist(2,6), dist(2,4)),
dist(5,3), dist(5,6), dist(5,4))
= max(0.15, 0.25, 0.20, 0.28, 0.39, 0.29)
= 0.39
0.34
63

64. Cluster Similarity: MAX or Complete Linkage
3 6 4 1 2 5
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
1
2
3
4
5
6
1
3 5
2
4
Dist({2,5,1},{3,6,4}) = max(dist(2,3), dist(2,6), dist(2,4)
dist(5,3), dist(5, 6), dist(5,4)
dist(1,3), dist(1,6), dist(1,4))
= max(0.15, 0.25, 0.20, 0.28, 0.39,
0.29, 0.22, 0.23,0.37)
=0.39
0.39
64

65. Strength of MAX
Original Points Two Clusters
• Less susceptible to noise and outliers
65

66. Limitations of MAX
Original Points Two Clusters
•Tends to break large clusters
•Biased towards globular clusters
66

67. Cluster Similarity: Group Average
• Group average Hierarchical
Clustering
Single link
compete link
67

68. Cluster Similarity: Group Average
Linkage
1
2
3
4
5
6
1
3 6 4 1 2 5
0
0.05
0.1
0.15
0.2
0.25
2 5 1
0.11
68

69. Cluster Similarity: Group Average
1
2
3
4
5
6
1
Dist({3,6},{1}) = avg(dist(3,1), dist(6,1)) = (0.22+0.23)/(2*1) = 0.225
Dist ({3,6},{2}) = avg(dist(3,2), dist(6,2)) = (0.15+0.25)/(2*1) = 0.20
Dist({3,6},{4}) = avg(dist(3,4), dist(6,4)) = (0.15+0.22)/(2*1) = 0.185**
Dist({3,6}, {5}) = avg(dist(3,5), dist(6,5)) = (0.28+0.39)/(2*1) = 0.335
3 6 4 1 2 5
0
0.05
0.1
0.15
0.2
0.25
2 5 1
0.11
69

70. Cluster Similarity: Group Average
1
2
3
4
5
6
1
2
Dist({3,6},{4}) = avg(dist(3,4), dist(6,4)) = (0.15+0.22)/(2*1) = 0.185** >
Dist({2}, {5})
3 6 4 1 2 5
0
0.05
0.1
0.15
0.2
0.25
2 5 1
0.14
70

71. Cluster Similarity: Group Average
1
2
3
4
5
6
1
2
3
3 6 4 1 2 5
0
0.05
0.1
0.15
0.2
0.25
2 5 1
Dist({3,6},{1}) = avg(dist(3,1), dist(6,1)) = (0.22+0.23)/(2*1) = 0.225
Dist ({3,6},{2}) = avg(dist(3,2), dist(6,2)) = (0.15+0.25)/(2*1) = 0.20
Dist({3,6},{4}) = avg(dist(3,4), dist(6,4)) = (0.15+0.22)/(2*1) = 0.185**
Dist({3,6}, {5}) = avg(dist(3,5), dist(6,5)) = (0.28+0.39)/(2*1) = 0.335
0.185
71

72. Cluster Similarity: Group Average
1
2
3
4
5
6
1
2
3
3 6 4 1 2 5
0
0.05
0.1
0.15
0.2
0.25
2 5 1
Dist({3,6, 4},{1}) = avg(dist(3,1), dist(6,1), dist(4,1))
= (0.22+0.23+0.37)/(3*1) = 0.273
Dist ({3,6,4},{2,5}) = avg(dist(3,2), dist(3,5), dist(6,2), dist(6,5),
dist(4,2), dist(4,5))
= (0.15+0.28+0.25+0.39+0.20+0.29)/(3*2)
= 0.26
4
0.26

73. Cluster Similarity: Group Average
1
2
3
4
5
6
1
2
5
3
3 6 4 1 2 5
0
0.05
0.1
0.15
0.2
0.25
2 5 1
4
Dist ({3,6,4,2,5}, {1}) = avg(dist(3,1), dist(6,1), dist(4,1), dist(2,1),dist(5,1))
= (0.22+0.23+0.37+0.24+0.34)/(5*1)
= 0.28
0.28
73

74. Hierarchical Clustering: Group
Average
• Compromise between Single and Complete
Link
• Strengths
– Less susceptible to noise and outliers
• Limitations
– Biased towards globular clusters
74

75. Hierarchical Clustering:
Comparison
Group Average
MIN MAX
1
2
3
4
5
6
1
2
5
3
4
1
2
3
4
5
6
1
2 5
3
41
2
3
4
5
6
1
2
3
4
5
75

76. Hierarchical Clustering:
Comparison
3 6 4 1 2 5
0
0.05
0.1
0.15
0.2
0.25
2 5 1
Group Average
3 6 4 1 2 5
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
MAX
3 6 2 5 4 1
0
0.05
0.1
0.15
0.2
MIN
76

77. Internal Measures : Cohesion and
Separation
(graph-based clusters)• A graph-based cluster approach can be evaluated by
cohesion and separation measures.
– Cluster cohesion is the sum of the weight of all links within a
cluster.
– Cluster separation is the sum of the weights between nodes in the
cluster and nodes outside the cluster.
cohesion separation
77

78. Cohesion and Separation (Central-
based clusters)
• A central-based cluster approach can be
evaluated by cohesion and separation
measures.
78

79. Cohesion and Separation (Central-
based clustering)
• Cluster Cohesion: Measures how closely related are
objects in a cluster
– Cohesion is measured by the within cluster
sum of squares (SSE)
• Cluster Separation: Measure how distinct or well-
separated a cluster is from other clusters
– Separation is measured by the between cluster
sum of squares
»Where |Ci| is the size of cluster i
i Cx
i
i
mxWSS 2
)(
i
ii mmCBSS 2
)(
79

80. Example: Cohesion and Separation
 Example: WSS + BSS = Total SSE (constant)
1 2 3 4 5
m
1091
9)5.43(2)5.13(2
1)5.45()5.44()5.12()5.11(
22
2222
Total
BSS
WSSK=2 clusters:
10010
0)33(4
10)35()34()32()31(
2
2222
Total
BSS
WSSK=1 cluster:
1 2 3 4 5m1 m2
m

81. HW#8
81
• Database Segmentation
K-means clustering K=3
C1 = (1,5)
, C2 = (3,12) C3 = (2,13)
(Pattern)
K-means

82. HW#8
82
• What is cluster?
• What is Good Clustering?
• How many types of clustering?
• How many Characteristics of Cluster?
• What is K-means Clustering?
• What are limitations of K-Mean?
• Please explain method of Hierarchical
Clustering?

83. ID X Y
A1 1 5
A2 4 9
A3 8 15
A4 6 2
A5 3 12
A6 10 7
A7 7 7
A8 11 4
A9 13 10
A10 2 13

84. LAB 8
84
• Use weka program to construct a neural
network classification from the given file.
• Weka Explorer  Open file  bank.arff
• Cluster  Choose button 
SimpleKMeans  Next, click on the text
box to the right of the "Choose" button to
get the pop-up window