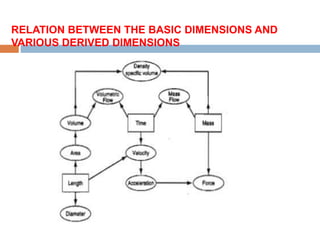
The document discusses the principles of units and dimensions in chemical engineering, explaining the difference between fundamental and derived units. It describes various systems of units, including SI, CGS, FPS, and BE, alongside their practical benefits and operational rules for unit conversions. Additionally, the document provides examples and exercises related to the conversion of units and their application in problem-solving.

2. CHEMICAL
PROCESS
PRINCIPLE-I
CHE-120
3 CREDIT HOURS Department of Chemical
Engineering,
Engr. Khurram Shahzad

3. LECTURE 2

4. What are Units and Dimensions
and How they Differ?
Dimensions are our basic concepts of
measurement such as length, time, mass,
temperature, and so on;
Units are the means of expressing the
dimensions, such as feet or centimeter for
length, and hours or second for time.
Units can be defined by convention, custom or
law.

5. Practical Benefits
a. Diminished possibility of error in your
calculations.
b. Reduce intermediate calculation and time in
solving
c. A logical approach to the problem rather than
remembering formula
d. Easy interpretation of the physical meaning of
the numbers you use.

6.  Fundamental (or basic) dimensions/units are
those that can be measured independently
and are sufficiently to describe essential
physical quantities.
 Derived dimensions/units are those that can
be developed in term of the fundamental
dimensions/units.
 Figure 1.1 illustrates the relation between the
basic dimensions and some of the derived
dimensions.

7. System Length Time Mass Force Energy Temperature
System
International (SI)
•Acceptance in the
Scientific and
engineering
Community
•Prefix are used
meter sec Kg Newton Joule C 0, K
CGS •Identical to SI
•Principal difference
gm and cm are used
instead of Kg and m.
centimet
er
sec gram dyne Erg C0 , K
FPS foot sec lbm Poundal ft. poundal F 0, R0
British
Engineering
system (BE)
foot sec Slug lbf Ft.lbf F0 ,R0
American
Engineering
system(AE)
• Conversion factors
are not multiple of 10
•Conversion factors are
taking ratios of
quantities
foot sec lbm lbf Btu F0 ,R0
SYSTEMS OF UNITS

10.  Dyne: One dyne is the force necessary to impart to a mass of an
acceleration of 1cm/s2.
F =ma
Dyne = 1gm.cm/s2 = gm.cm s-2
= [MLT-2]
 Newton: Newton is the force necessary to impart to a mass of 1 Kg
an acceleration of 1m/s2.
F = ma
N = m/s2 = Kgms-2 = [MLT-2]
 Joule: One joule is amount of work done when a force of 1N acting
on a body displaces it through a distance of 1m along the direction
of force i.e.
Joule = N .m = Kg m/s2 .m = Kgm2. S-2
1 joule = 107 erg J > erg
 Erg: It is the amount of work done when a force of I dyne acting on
body displaces it through a distance of 1cm along the direction of
force.

11.  Poundal(Pdl): It is define as the force require it gives a mass of one
pound and acceleration of 1ft/s2.
1 poundal = 1lbm.1ft/s2
 Lbf: It is defined as the force required to give a mass of 1 pound an
acceleration of 32.174 ft/s2.
1 lbf = 32.174 lbm ft/s2
:.as lbm ft/s2 = 1 poundal
1lbf = 32.174 poundal
1lbf = 4.44 x 105 dyne =4.44 N
1 N = 105 dyne
 Slug: It is defined as the mass which is given an acceleration of
1ft/s2 by 1lbf.
F = ma
m = F/a (slug = 1lbf/ft/s2)
slug = lbf s2ft-1
1 slug = 32.174 lbm

12. Operations with Unit
 Units can be treated like algebraic variables
 Numerical values of two quantities may be
added or subtracted only if the units are same.
3cm-1 cm=2cm (3x-x=2x)
But
3cm-1 mm (or s)=? (3x-y=?)

13.  Numerical values and their corresponding
units may always be combined by
multiplication and division
3N X 4 m= 12N.m
5 km =2.5km/h
2.0h
7 km/h X 4 h = 28 km
3 m X 4 m = 12m2

14. Example 1.1
Add the following
(a) 1 foot + 3 seconds
(b) 1 horsepower + 300watts

15. RELATION BETWEEN THE BASIC DIMENSIONS AND
VARIOUS DERIVED DIMENSIONS

16. Conversion of Units and
Conversion Factors
 Conversion Factor: is a term by which units
are multiplied to obtain units in another system
or in more convenient form
Example: 2.54 cm/inch , on squaring the term
give 6.45cm2/inch2,
 not only the value is squared but units are also
raised to the same power
 on cubing the term gives 16.38 cm3/inch3.

17.  Multiplication Symbol
3N X 4 m= 12N.m
 Use of a Special Format, Vertical line instead
of the multiplication symbol
Example: If a plane travels at twice the speed of
sound (assume that the speed of sound is
1100 ft/sec), how fast is it going in miles/hr.

18. 1. If a plane travels twice the speed of sound (assume
that the speed of sound is 1100 ft/sec.) how fast is it
going in miles/hr.
2. Change 400 inch3/day to cm3/min.
3. Convert 760 mm of Hg to inches of Hg.
4. Convert an acceleration of 1 cm/sec2 to its equivalent
in Km/yr2.
5. Convert 23 lb mass. ft/min2 tp its equivalent in Kg
cm/sec.
6. Express 1.80 gms/cm3 to its equivalent lbm /gallons
7. The viscosity of a certain is 0.000672 lb/ft.sec convert
its to metric units gm/cm.hr .
Practic
e