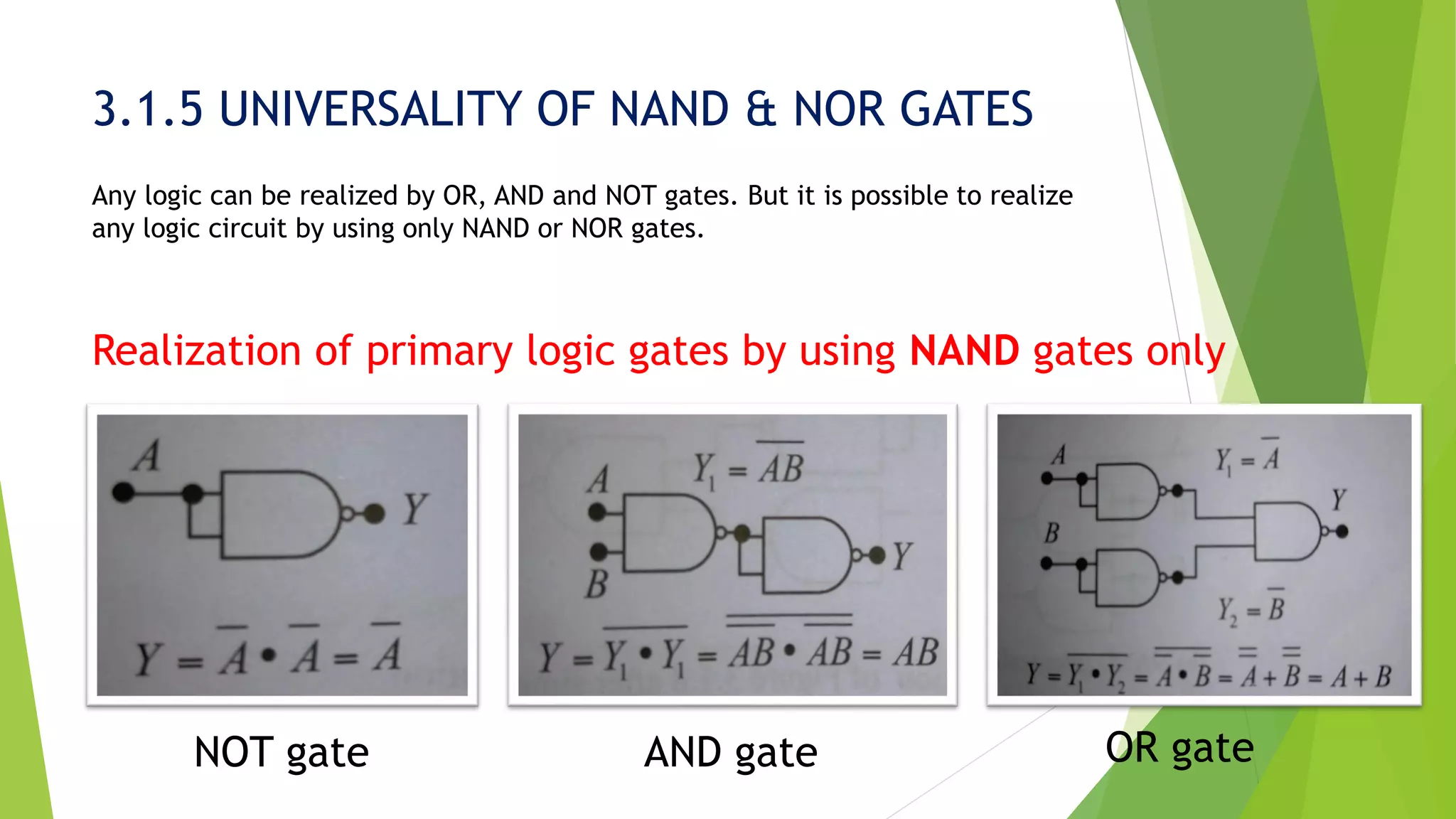
The document covers the fundamentals of logic gates, including primary gates like AND, OR, and NOT, as well as secondary gates such as NAND, NOR, XOR, and XNOR. It explains Boolean theorems, De Morgan's theorems, and the universality of NAND and NOR gates in constructing logic circuits. Additionally, practice questions are included to test understanding of the concepts presented.

1. Course Name: COMPUTER FUNDAMENTAL
Lesson 3.1
LOGIC FUNDAMENTALS
Presented by
MIR ANUPAM HOSSAIN AKIB
Department of Software Engineering
ID: 191-35-2640, 28th Batch

2. 3.1.1 INTRODUCTION
Data and control instructions move inside a computer by means of pulse of
electricity
Pulses of electricity are called digital signals.
George Boole introduced the concept of binary system in 1854
A logic gate is a circuit which uses digital signals as its inputs and outputs.
HIGH and LOW levels of a pulse can also be represented by binary 1 or 0
respectively

3. 3.1.2 LOGIC GATES
# Primary Logic Gates:
❖ OR
❖ AND
❖ NOT
# Secondary Logic Gates:
▪ NAND
▪ NOR
▪ EXOR
▪ EXNOR

4. PRIMARY LOGIC GATE
3.1.2 Logic Gates

5. 3.1.2 LOGIC GATES (Primary)
OR Gate:
• OR operation is denoted by (+) A B Y = A+B
0 0 0
0 1 1
1 0 1
1 1 1
• A HIGH (1) output results if one or all the inputs of the gate are HIGH (1).
• If neither input is HIGH, a LOW output results.
Truth Table of OR Gate

6. 3.1.2 LOGIC GATES (Primary)
AND Gate:
• AND operation is denoted by multiple (*)
A B Y = A.B
0 0 0
0 1 0
1 0 0
1 1 1
• A HIGH (1) output results if all the inputs of the gate are HIGH (1).
• If one input is LOW (0) then a LOW output results.
Truth Table of AND Gate
A
B
Y=A.B

7. 3.1.2 LOGIC GATES (Primary)
NOT Gate:
• The NOT gate produces an inverted version of the input at its output
• It is also known as an inverter.
• If the input variable is A, the inverted output is called NOT A
Truth Table of NOT Gate
A Y = ഥ𝑨
0 1
1 0

8. SECONDARY LOGIC GATE
3.1.2 Logic Gates

9. 3.1.2 LOGIC GATES (Secondary)
NAND Gate:
Truth Table of NAND Gate
NOT + AND = NAND ☺
Y = 𝑨𝑩
A B Y = 𝑨𝑩
0 0 1
0 1 1
1 0 1
1 1 0
▪ This is equivalent to an AND gate followed by a NOT gate.
▪ The output of a NAND gate is high if any one of the inputs is low or all the inputs are low
▪ The symbol is an AND gate with a small circle on the output. The small circle represents
invertion.

10. 3.1.2 LOGIC GATES (Secondary)
NOR Gate:
Truth Table of NOR Gate
NOT + OR = NOR ☺
Y = 𝑨 + 𝑩
A B Y = 𝑨 + 𝑩
0 0 1
0 1 0
1 0 0
1 1 0
▪ This is equivalent to an OR gate followed by a NOT gate.
▪ The output of a NOR gate is LOW if any one of the inputs is HIGH or all the inputs are
HIGH
▪ The symbol is an OR gate with a small circle on the output. The small circle represents
invertion.

11. 3.1.2 LOGIC GATES (Secondary)
EXOR (Exclusive-OR) Gate:
Truth Table of EXOR Gate
A B Y = A ⊕ B
0 0 0
0 1 1
1 0 1
1 1 0
❖ The ‘Exclusive-OR’ gate is a circuit which will give a high output if either, but
not both, of its two inputs are high.
❖ An encircled plus sign is used to show the EXOR operation.
A
B
Y = A ⊕ B

12. 3.1.2 LOGIC GATES (Secondary)
EXNOR (Exclusive-NOR) Gate:
Truth Table of EXNOR Gate
A B Y = A ⊕ B
0 0 1
0 1 0
1 0 0
1 1 1
❖ The ‘Exclusive-NOR’ gate circuit does the opposite to the EXOR gate
❖ It will give a low output if either, but not both, of its two inputs are high.
❖ The symbol is an EXOR gate with a small circle on the output.
A
B
Y = A ⊕ B

13. BOOLEAN THEOREMS
3.1.3 Boolean Theorems

14. 3.1.3 BOOLEAN THEOREMS
Logic circuits can be simplified by Boolean algebra and simplification of logic functions
and logic circuits is an important application of Boolean algebra. Important Boolean
Theorems are given in the table.
Theorems based on AND logic Example
1. A.0 = 0 1.0 = 0
0.0 = 0
2. A.1 = A 1.1 = 1
0.1 = 0
3. A.A = A 1.1 = 1
0.0 = 0
4. A. ഥ𝑨 = 0 1.0 = 0
0.1 = 0
5. A.B = B.A [Commutative Law]
6. A.B.C = (A.B).C = A.(B.C) [Associative Law]

15. 3.1.3 BOOLEAN THEOREMS
Theorems based on OR logic Example
1. A + 0 = A 1 + 0 = 1
0 + 0 = 0
2. A + 1 = 1 1 + 1 = 1
0 + 1 = 1
3. AA = A 1 + 1 = 1
0 + 0 = 0
4. A + ഥ𝑨 = 1 1 + 0 = 1
0 + 1 = 1
5. A+B = B+A [Commutative Law]
6. A+B+C = (A+B)+C = A+(B+C) [Associative Law]

16. 3.1.3 BOOLEAN THEOREMS
Distributed Law
1. A.(B+C) = A.B + A.C
2. A+(B.C) = (A+B).(A+C)
Redundancy Law
1. A + (A.B) = A
2. A.(A + B) = A

17. 3.1.3 BOOLEAN THEOREMS
Example: Simplify Y = A . (B + C) . ഥ𝑨 . B . D
Given,
Y = A . (B + C) . ഥ𝑨 . B . D
= A . ഥ𝑨 . (B + C) . B . D
= 0 [As A . ഥ𝑨 = 0] (answer)
Your Work:
Simplify it, Y = (A + B) . (A + B) + C

18. DE MORGAN’S THEOREMS
3.1.4 De Morgan’s Theorems

19. 3.1.4 DE MORGAN’S THEOREMS
French Mathematics De Morgan formulated two theorems in 1953 and the known as
De Morgan’s theorems. For two variables, De Morgan’s theorem can be written as
𝑨 + 𝑩 = ഥ𝑨 . ഥ𝑩
𝑨. 𝑩 = ഥ𝑨 + ഥ𝑩
For three variables, it can be written as
𝑨 + 𝑩 + 𝑪 = ഥ𝑨 . ഥ𝑩 . ഥ𝑪
𝑨. 𝑩. 𝑪 = ഥ𝑨 + ഥ𝑩 + ഥ𝑪

20. 3.1.4 DE MORGAN’S THEOREMS
A B 𝑨 + 𝑩 ഥ𝑨 . ഥ𝑩 Remark 𝑨. 𝑩 ഥ𝑨 + ഥ𝑩 Remark
0 0 1 1 1 1
0 1 0 0 1 1
1 0 0 0 1 1
1 1 0 0 0 0
De Morgan’s
theorem
𝑨 + 𝑩 = ഥ𝑨 . ഥ𝑩
Is verified
De Morgan’s
theorem
𝑨. 𝑩 = ഥ𝑨 + ഥ𝑩
Is verified
The proof of the De Morgan’s theorems for two variables using
truth table is as follows

21. UNIVERSALITY OF NAND & NOR GATES
3.1.5 Universality Of NAND & NOR Gates

22. 3.1.5 UNIVERSALITY OF NAND & NOR GATES
Any logic can be realized by OR, AND and NOT gates. But it is possible to realize
any logic circuit by using only NAND or NOR gates.
Realization of primary logic gates by using NAND gates only
NOT gate AND gate OR gate

23. 3.1.5 UNIVERSALITY OF NAND & NOR GATES
Any logic can be realized by OR, AND and NOT gates. But it is possible to realize
any logic circuit by using only NAND or NOR gates.
Realization of primary logic gates by using NOR gates only
NOT gate AND gate

24. SOME QUESTIONS

25. 3.1.7 SOME QUESTIONS (PRACTICE)
1. An OR function is denoted by_________.
a) X
b) .
c) /
d) +
2. The primary gates are_______.
a) OR, AND, NAND
b) NOR, NOT, AND
c) OR, AND, NOT
d) NOR, NAND, EX-OR
3. The pulses of electricity represents_________ signal.
a) Voltage
b) Analog
c) Current
d) Digital
✓
✓
✓

26. THANK YOU