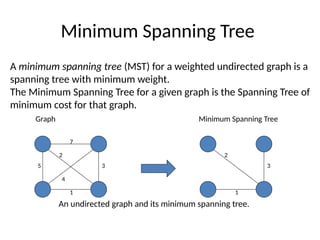
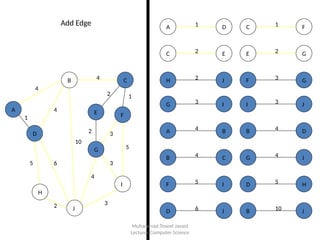
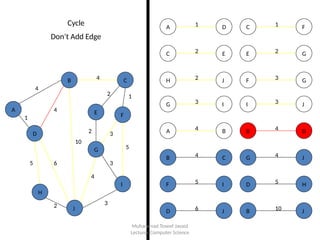
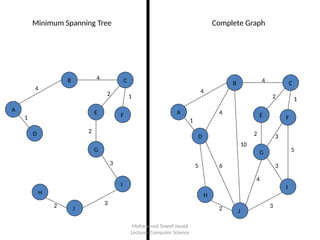
The document discusses the concept of Minimum Spanning Trees (MST) in graph theory, specifically detailing Kruskal's and Prim's algorithms used to find MSTs. It explains that an MST is a spanning tree that connects all vertices in a graph with the minimum total edge weight. The document outlines the steps of Kruskal's algorithm, focusing on connecting nodes while avoiding cycles to achieve the minimum weight spanning tree.

1. Minimum Spanning Tree
Muhammad Toseef Javaid
Lecturer Computer Science

2. Today Topic
• We will study Minimum Spanning Tree using
Kruskal Algorithm
Prim’s Algorithm
Muhammad Toseef Javaid
Lecturer Computer Science

3. Muhammad Toseef Javaid
Lecturer Computer Science

7. Wiring: Naïve Approach
Central office
Expensive!

8. Wiring: Better Approach
Central office
Minimize the total length of wire connecting the customers

9. Minimum Spanning Tree (MST)
• it is a tree (i.e., it is acyclic)
• it covers all the vertices V
– contains |V| - 1 edges
• the total cost associated with tree edges is the
minimum among all possible spanning trees
• not necessarily unique
A minimum spanning tree is a subgraph of an
undirected weighted graph G, such that

10. Spanning Trees
• A spanning tree of an undirected graph G is a
sub graph of G that is a tree containing all the
vertices of G.
• In a weighted graph, the weight of a sub graph
is the sum of the weights of the edges in the
sub graph.
or or or
Some Spanning Trees from Graph A
Graph A

11. Minimum Spanning Tree
A minimum spanning tree (MST) for a weighted undirected graph is a
spanning tree with minimum weight.
The Minimum Spanning Tree for a given graph is the Spanning Tree of
minimum cost for that graph.
5
7
2
1
3
4
2
1
3
Graph Minimum Spanning Tree
An undirected graph and its minimum spanning tree.

12. Minimum Spanning Tree
• A tree (a connected graph with no
cycles) which connects all the nodes
together is called a Spanning Tree
• For any connected graph with n nodes,
each spanning tree will have n - 1 arcs
• The Minimum Spanning Tree is the one
with the Minimum weight

13. Algorithms for Obtaining the Minimum
Spanning Tree
• Kruskal's Algorithm
• Prim's Algorithm

14. • Kruskal’s algorithm qualifies as a greedy
algorithm because at each step it adds to the
forest an edge of least possible weight.

15. Kruskal's Algorithm
This algorithm creates a forest of trees. Initially the forest
consists of n single node trees (and no edges). At each step,
we add one edge (the cheapest one) so that it joins two trees
together. If it were to form a cycle, it would simply link two
nodes that were already part of a single connected tree, so
that this edge would not be needed.

16. Kruskal’s Algorithm
• Step 1: . The forest is constructed - with each node in a separate
tree
• Step 2: The edges are placed in a priority queue.
• Step 3: Until we've added n-1 edges,
1. Extract the cheapest edge from the queue,
2. If it forms a cycle, reject it,
3. Else add it to the forest. Adding it to the
forest will join two trees together.
• Every step will have joined two trees in the forest together, so that
at the end, there will only be one tree in T.
Aim: To find a minimum spanning tree for a connected
graph with n nodes:

17. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Complete Graph

18. 1
4
2
5
2
5
4
3
4
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
A A
B D
B B
B
C D
J C
C
E
F
D
D H
J E G
F F
G I
G G
I J
H J J
I

19. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
J
I
1
A D
4
B C
4
A B
Sort Edges
(in reality they are placed in a priority
queue - not sorted - but sorting them
makes the algorithm easier to visualize)

20. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
J
I
1
A D
4
B C
4
A B
Add Edge
Muhammad Toseef Javaid
Lecturer Computer Science

21. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
J
I
1
A D
4
B C
4
A B
Add Edge
Muhammad Toseef Javaid
Lecturer Computer Science

22. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
J
I
1
A D
4
B C
4
A B
Add Edge
Muhammad Toseef Javaid
Lecturer Computer Science

23. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
J
I
1
A D
4
B C
4
A B
Add Edge
Muhammad Toseef Javaid
Lecturer Computer Science

24. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
J
I
1
A D
4
B C
4
A B
Add Edge
Muhammad Toseef Javaid
Lecturer Computer Science

25. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
J
I
1
A D
4
B C
4
A B
Cycle
Don’t Add Edge
Muhammad Toseef Javaid
Lecturer Computer Science

26. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
J
I
1
A D
4
B C
4
A B
Add Edge
Muhammad Toseef Javaid
Lecturer Computer Science

27. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
J
I
1
A D
4
B C
4
A B
Add Edge
Muhammad Toseef Javaid
Lecturer Computer Science

28. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
J
I
1
A D
4
B C
4
A B
Add Edge
Muhammad Toseef Javaid
Lecturer Computer Science

29. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
J
I
1
A D
4
B C
4
A B
Cycle
Don’t Add Edge
Muhammad Toseef Javaid
Lecturer Computer Science

30. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
J
I
1
A D
4
B C
4
A B
Add Edge
Muhammad Toseef Javaid
Lecturer Computer Science

31. 4
1
2
2 1
3
3
2
4
A
B C
D
E F
G
H
I
J
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Minimum Spanning Tree Complete Graph
Muhammad Toseef Javaid
Lecturer Computer Science