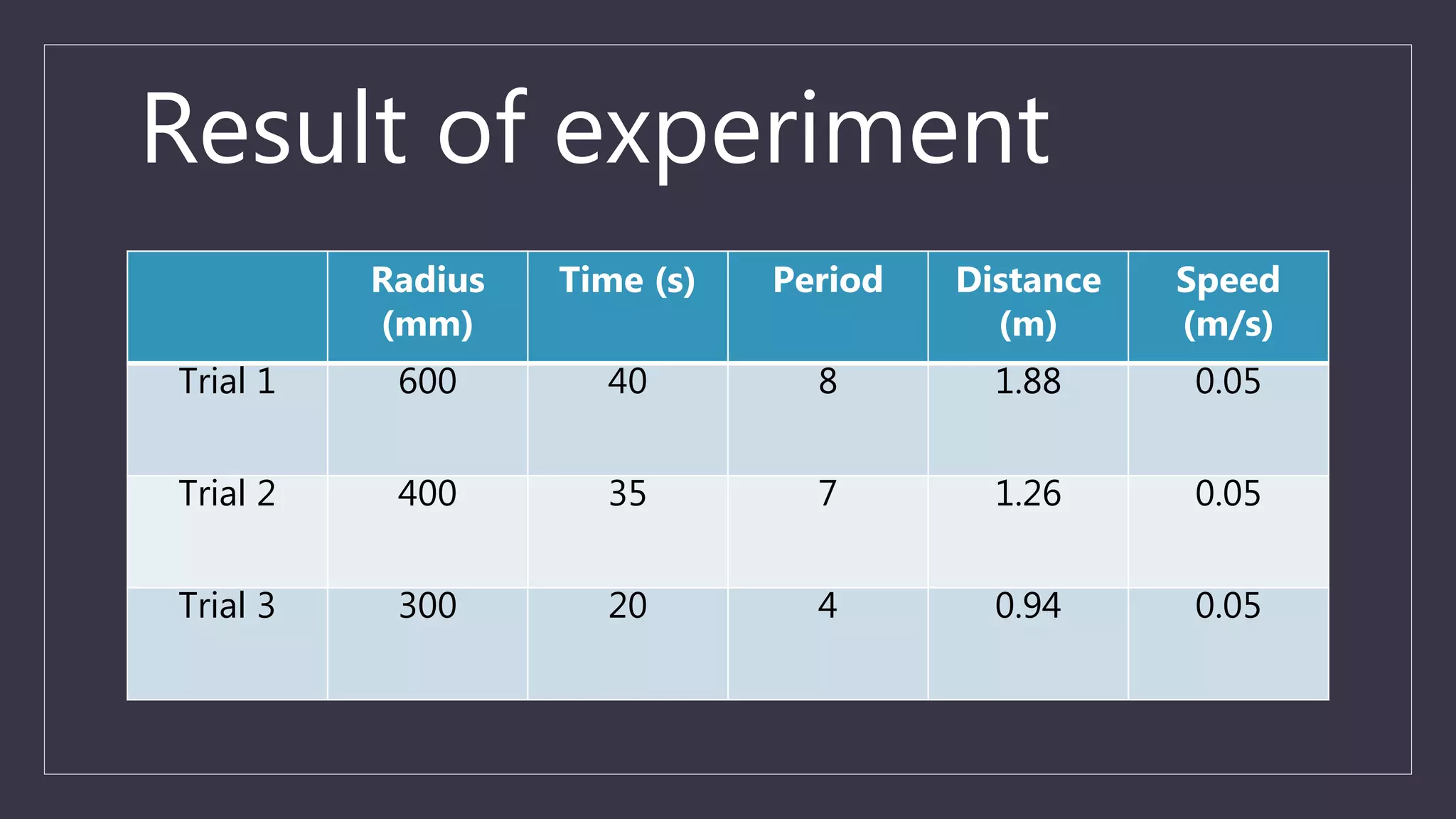
The document summarizes experiments on centripetal force using a rotating platform. It discusses the centripetal force needed to maintain circular motion and provides formulas for calculating centripetal acceleration and force. Examples are given about centripetal force in a rotating train and questions are provided about centripetal force exerted on a hanging penny and problems calculating force for given mass, speed, and radius.

1. CRECALL

2. Result of experiment
Radius
(mm)
Time (s) Period Distance
(m)
Speed
(m/s)
Trial 1 600 40 8 1.88 0.05
Trial 2 400 35 7 1.26 0.05
Trial 3 300 20 4 0.94 0.05

3. Questions:
•What makes the car revolve from the center?
•What do you think will happen if the string is cut?

4. Centripetal Force
The centripetal force is the force that is
center-seeking, it maintains the circular
path of an object.
Play

5. Questions:
•What have you noticed with the objects shown
in the video?
•What makes those objects keep their circular
path?
•Is there any other factor that helps such objects
to do what they are actually doing?

6. CHANG A PENNY

7. Questions:
1. What makes the penny to be remained attached to
the hanger while the hanger is rotating?
2. Which of the materials exerts centripetal force?

8. C
CENTRIPETAL
ACCELERATION
AND FORCE

9. Objectives
1. Define centripetal force and centripetal acceleration
2. Cite objects where centripetal force exists
3. Solve problems involving centripetal force and acceleration

10. Centripetal Acceleration
Change in velocity per unit of time in a uniform circular
motion
Always directed towards the center of the curvature
“center-seeking” acceleration
Magnitude of tangential velocity is the same as the
magnitude of tangential speed but both have different
direction

11. Formula
𝑎 𝑐 =
𝑣2
𝑟
or
𝑎 𝑐 = 𝑟𝑤2
𝑎 𝑐- centripetal acceleration (m/s2)
v- tangential speed (m/s)
r- radius
w- rotational speed (rad/s)

12. Centripetal Force
It is the “center-seeking” force
It is the force that maintains the circular path
of the object.

13. Formula
From
F=ma
Centripetal force becomes
Fc = m ac
Fc – centripetal force
m- mass
ac – centripetal acceleration

14. Using tangential and rotational
speed…
𝐹𝑐 =
𝑚𝑣2
𝑟
or
𝐹 = 𝑚𝑟𝑤2

15. Sample problem:
Solve for the centripetal force of an 8000kg train whose speed
is 100km/h that rounds a curve whose radius is 150m.

16. Reflection
Since the centripetal force talks about a circular motion
and an object traveling a circular path will continue to have its
path as long as the centripetal force is present, this means an
endless thing and a cycle that you will go back from where you
started. Sometimes in life, when work seems to be endless and
problems keep coming back, we need to persevere more and
be patient. It has never been easy to be patient, but it’s
probably harder now than any time in history. Have you tested
your patience? How? What does it bring you? Is it true that
patience is a virtue?

17. Seatwork:
1. What is the centripetal force of a point on the rim of a 0.90m
flywheel in diameter, turning at the rate of 1200rad/min?
2. If the weight of a car traveling with a speed of 100km is 1.44
x 104 then the radius is 150m, what would be the necessary
force?