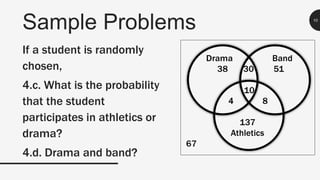
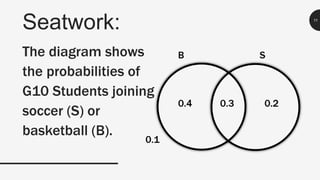
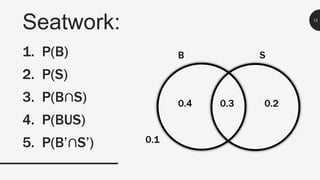
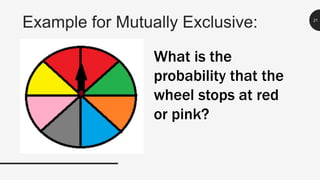
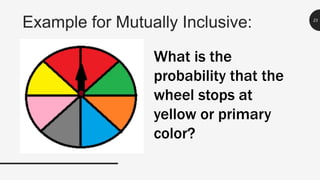
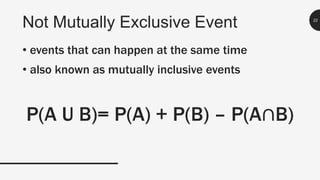This document discusses probability and different types of events. It defines key terms like experiment, outcome, and sample space. It explains that simple events consist of one outcome while compound events have more than one outcome. It provides examples of calculating probabilities of simple, compound, mutually exclusive and not mutually exclusive events using diagrams, dice rolls, cards, and student activities data. Sample problems are worked through and explained.

1. MODULE 7
PROBABILITY
OF AN EVENT
Simple and Compound Events

2. Probability
Probability=
𝑛𝑜.𝑜𝑓 𝑤𝑎𝑛𝑡𝑒𝑑 𝑜𝑢𝑡𝑐𝑜𝑚𝑒𝑠
𝑛𝑜.𝑜𝑓 𝑝𝑜𝑠𝑠𝑖𝑏𝑙𝑒 𝑜𝑢𝑡𝑐𝑜𝑚𝑒𝑠
2
• Ratio where the number of how many times an
outcome can occur was compared to the number of
all possible outcomes

3. Definition of Terms 3
• Experiment- doing the activity over and
over again
• Outcome- result of the experiment
• Sample space- number of all outcomes

4. Types of Events: 4
•Simple- consist of 1 outcome
•Compound- consist of more
than 1 outcome

5. Sample Problems 5
1. What is the probability of
getting no. 6 when you roll a
dice?

6. Sample Problems 6
2. What is the probability of
getting 4s when you roll 3 dice?

7. Sample Problems 7
3. What is the probability of
getting 2 red cards in a deck of
cards?

8. Sample Problems 8
4. Seniors of CIS join
different
extracurricular
activities shown in
the diagram:

9. Sample Problems 9
4. a. How many are
seniors in CIS?
4.b. How many
students participate
in athletics?

10. Sample Problems 10
If a student is randomly
chosen,
4.c. What is the probability
that the student
participates in athletics or
drama?
4.d. Drama and band?

11. Seatwork: 11
The diagram shows
the probabilities of
G10 Students joining
soccer (S) or
basketball (B).

12. Seatwork: 12
1. P(B)
2. P(S)
3. P(B∩S)
4. P(BUS)
5. P(B’∩S’)

13. Quiz: 13
In a group of students, 65 play football, 45 play
hockey, 52 play cricket, 20 play football and hockey,
25 play football and cricket, 15 play hockey and
cricket and 8 play all three games. Let F, H and C
represent the students who play football, hockey and
cricket, respectively.

14. Find the following: 14
1.How many students play all the
games?
2.How many played football only?
3.Hockey only?
4.Cricket only?

15. If a student is chosen at random, find the
probability that the student plays:
15
5. Football?
6. Hockey?
7. Cricket?
8. Football and hockey?
9. Hockey only?
10. Hockey and cricket?

16. Activity: Give Me Something 16
1.Blue or red
2.Round or rectangular
3.Round and blue
4.Round and rectangular

17. Mutually Exclusive and
Not Mutually Exclusive
Events
17

18. Analysis: 18
• Say I have a bowl containing 15 chips numbered 1 to 15,
what is a probability if I randomly choose a ball numbered
7 or 15?
• What about even or divisible by 3?

19. Questions: 19
• Is there a difference between the solution to the two
questions?
• How do you differentiate mutually exclusive to
mutually inclusive events?

20. Mutually Exclusive Event 20
• events that cannot happen at the same time
P(A U B)= P(A) + P(B)

21. Example for Mutually Exclusive: 21
What is the
probability that the
wheel stops at red
or pink?

22. Not Mutually Exclusive Event 22
• events that can happen at the same time
• also known as mutually inclusive events
P(A U B)= P(A) + P(B) – P(A∩B)

23. Example for Mutually Inclusive: 23
What is the
probability that the
wheel stops at
yellow or primary
color?

24. Sample Problem: 24
What is the probability of drawing a
black card or a ten in a deck of
cards?

25. Seatwork: 25
A bowl containing 15 chips numbered
1 to 15, what is a probability if a ball
was randomly chosen:
1. With 1 or an even number?
2. With odd number & divisible by 5?