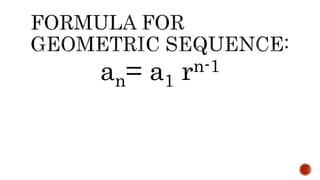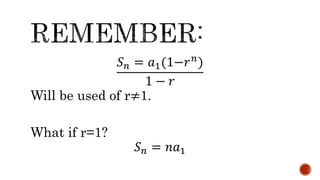The document provides information about arithmetic and geometric sequences. It defines arithmetic sequences as sequences where each term is obtained by adding a constant (the common difference) to the preceding term. Geometric sequences are defined as sequences where each term is obtained by multiplying the preceding term by a constant (the common ratio). Formulas are provided for finding specific terms, sums of terms, and other properties of arithmetic and geometric sequences. Examples of solving various arithmetic and geometric sequence problems are also presented.

1. P A T T E R

2. 1. What is the next shape?
, , , , , , ,
____________
2. What is the next number?
0, 4, 8, 12, 16, _______
3. What is the 7th number?
160, 80, 40, 20, 10, …?

3. Is a function whose domain is either
finite set or infinite set arranged in
order.

5. A= ( 5, 10, 15, 20, 30, 40)
B= (5, 10, 15, 20, 25, 30)

6. 1.𝑎𝑛 = 𝑛 + 4
2. 𝑎𝑛 = (−2)𝑛

7. Count the number of matchsticks in each figure and record
results on the table.
Number of
squares
1 2 3 4 5 6 7 8 9 1
0
Number of

8. A sequence where every term after
the first is obtained by adding a
constant called the common
difference

9. 1.17, 14, ___, ___, 5
2.13, ___, ___, ___, -11, -17

10. 𝑎𝑛 = 𝑎1 + 𝑛 − 1 𝑑

11. Finding the 10th term:
𝑎10=13+(10−1)−6
𝑎10= 13+ (9)-6
𝑎10= 13+ (9)-6
𝑎10= 13-54
𝑎10= -41

12. 1. Find the 13th term of the sequence 5, 8, 11,
…
2. Find the 6th term of the sequence 6, 3, 0, …
Name 𝑎1 𝑎𝑛𝑑 𝑑 first before solving. (3 points
each)

13. The terms between any two non-
consecutive terms of an arithmetic
sequence.

14. Insert 4 arithmetic means between 5 and 25.
𝑎1 = 5 𝑎6 = 25
Using the formula for arithmetic sequence,
𝑎6 = 𝑎1 + 6 − 1 𝑑
𝑎6 = 𝑎1 + 5 𝑑
25= 5 + 5𝑑
25-5= 5d
20= 5d
d=4

15. 𝑎2 = 𝑎1 + 2 − 1 𝑑
𝑎2 = 5 + 1 4
𝑎2 = 9
(5, 9, 13, 17, 21, 25)

16. Find 3 terms between 2 and 34 of an arithmetic
sequence.
a. Solve for d.
b. Solve for 𝑎2
c. Solve for 𝑎3
d. Solve for 𝑎4
e. What is the arithmetic sequence?

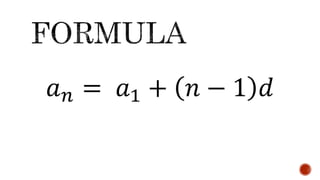
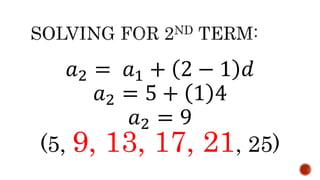
17. 𝑆𝑛 =
𝑛
2
(𝑎1 + 𝑎𝑛)
𝑆𝑛 =
𝑛
2
[𝑎1 + (𝑎1+ 𝑛 − 1 ]𝑑
𝑆𝑛 =
𝑛
2
[2𝑎1 + 𝑛 − 1 𝑑]

18. Find the sum of the first 10 terms of arithmetic
sequence 5, 9, 13, 17, …
To solve d,
d= 9 - 5= 4
Using the formula,
𝑆𝑛 =
𝑛
2
[2𝑎1 + 𝑛 − 1 𝑑]
𝑆𝑛 =
10
2
[2(5) + 10 − 1 4]
𝑆𝑛 = 5[10 + 9(4)]
𝑆𝑛 = 5 46 = 230

19. 1. Find the sum of the first 20 terms of
the arithmetic sequence -2, -5, -8, -11,
…
2. Find the sum of the first 7 terms of the
arithmetic sequence 6, 2, -2, -6, …

20. 1. The first term of an arithmetic sequence is 4 and the tenth term is
67.
What is the common difference? (1 pt.)
2. What is the thirty-second term of the arithmetic sequence -12, -7, -
2, 3, ... ? (2 pts.)
a. Find d b. Find 𝑎32
3. What is the sum of the first sixteen terms of the arithmetic
sequence
1, 5, 9, 13, ... ? (2 pts.)
a. Find d b. Find 𝑆16
4. What is the sum of the eleventh to twentieth terms (inclusive)of
the arithmetic sequence 7, 12, 17, 22, ... ? (Solve for d first before
finding the sum of 11th to 20th terms for 5 pts.)

21. 1. 2, 8
2. -3, 9
3. 1, ½
4. -5, -10
5. 12, 4

22. ARITHMETIC
SEQUENCE
5, 20, 80, 320, …

23. is a sequence where each term after the
first is obtained by multiplying the
preceding term by a non-zero constant
called common ratio.
Common ratio, r, can be determined by
dividing any term in a sequence that
precedes it.

24. 1. 5, 15, 45, 135, …
2. 7 2, 5 2, 3 2, 2, …
3.
1
3
,
2
3
,
3
3
,
4
3
, …
4. 5, −10, 20, −40
5. 8, 4, 2, 1, …

25. In arithmetic sequence, the
constant is the common
difference while in geometric
sequence, the constant is the
common ratio.

26. 1.3, 12, 48, ___, ___
2.¼, ___, ___, ___, 64, 256

27. an= a1 rn-1

28. What is the 10th term in the
geometric sequence 8, 4, 2, 1, …?

29. Find the 6th term of the geometric
sequence whose second term is 6 and
common ratio is 2.

30. Geometric means are the terms
between any two given terms in a
geometric sequence.

31. Insert three terms between 2 and
32 of a geometric sequence.

32. Insert two terms between 5 and
135 of a geometric sequence.

33. The geometric mean between the
first two terms in a geometric
sequence is 32. If the 3rd term is 4,
find the first term.

34. I. Fill in the blanks with the correct word found on
the box.
A geometric sequence contains term in which after
the first is obtained by __________ the preceding term
by a non-zero _____________ called common ratio. The
terms between any two terms in geometric sequence
is called ____________________. In every solution to a
geometric sequence, ______________ is the first thing
to be considered. In every geometric sequence,
___________________ serves to be the constant value.

35. II. Solve the following problems:
1. In the geometric sequence 6, 12, 24, 48, …, which term is 768?
a. Solve for r
b. Solve for n
2. Find k so that the terms k-3, k+1 and 4k-2 form a geometric sequence.
a. Solve for k
b. Solve for k-3, k+1 and 4k-2 (3pts)
c. Form a geometric sequence consisting of 5 terms
3. Find two geometric means between 2xy and 16xy4
a. Find r
b. Find the two geometric means (2 pts.)

36. Consider the geometric sequence 3, 6, 12, 24, 48, 96,
…, what is the sum of the first 5 terms?
a. Manually solve for the sum of the first 5 terms
b. Consider other solution below:
𝑆5 = 3 + 6 + 12 + 24 + 48
− 2𝑆5 = 6 + 12 + 24 + 48 + 96
−𝑆5= 3 − 96
𝑆5 = 93
How about if it will be applied in the formula?

37. 𝑆𝑛 = 𝑎1 + 𝑎1𝑟 + 𝑎1𝑟2 + 𝑎1𝑟3 + ⋯ + 𝑎1𝑟𝑛−1
−(r𝑆𝑛 = 𝑎1𝑟 + 𝑎1𝑟2 + 𝑎1𝑟3 + ⋯ + 𝑎1𝑟𝑛−1 + 𝑎1𝑟𝑛)
𝑆𝑛 − 𝑟𝑆𝑛 = 𝑎1 − 𝑎1𝑟𝑛
by factoring: 𝑆𝑛(1 − 𝑟) = 𝑎1(1−𝑟𝑛
)
1 − 𝑟
To get the sum:𝑆𝑛 =
𝑎1(1−𝑟𝑛)
1−𝑟

38. Find the sum of the first 4 terms of
the sequence 81, 27, 9, 3, 1, …

39. 𝑆𝑛 = 𝑎1(1−𝑟𝑛
)
1 − 𝑟
Will be used of r≠1.
What if r=1?
𝑆𝑛 = 𝑛𝑎1

40. -2, 2, -2, 2, -2, …
1. Find the sum of the first 5 terms
2. Find the sum of the first 8 terms
3. Find the sum of the first 4 terms
4. Find the sum of the first 3 terms
5. Find the sum of the first 7 terms

41. If r= -1, the sum Sn
simplifies to,
Sn= 0 if n is even
Sn= a1 if n is odd

42. 1.5 terms of 4, 12, 36, 108, … (2
pts)
2.6 terms of -3, 3, -3, 3, …
3.7 terms of 9, 9, 9, 9, 9, …
4.9 terms of 4, -4, 4, -4, ...