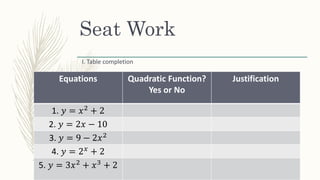
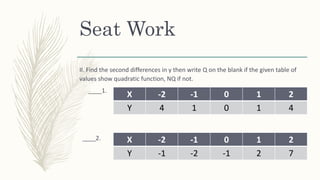
This document provides an introduction to quadratic functions including: - Quadratic functions can be described by equations of the form y = ax^2 + bx + c, where a, b, and c are real numbers and a ≠ 0. - The graph of a quadratic function is a parabola (smooth curve). - Tables of values for quadratic functions have a constant second difference in y. - Examples of quadratic and non-quadratic functions are provided along with practice problems identifying quadratic functions from equations and tables of values.

1. Introduction
to
Quadratic
Functions

2. Functions
– Set of number pairs of which no two first
numbers are the same
– One-to-one correspondence

3. Quadratic Functions
–Functions that can be described by
equations of the form
𝑦 = 𝑎𝑥2
+ 𝑏𝑥 + 𝑐
where a, b and c are real numbers and a
≠ 0.

4. Quadratic Functions
–Its graph is known as a parabola (a
smooth curve)
–Its table of values has a constant value
on the second differences in y

5. Consider the example below:
X -3 -2 -1 0 1 2 3
Y 5 0 -3 -4 -3 0 5
𝑦 = 𝑥2 − 4
5 3 1 -1 -3 -5
2 2 2 2 2

6. Seat Work
I. Table completion
Equations Quadratic Function?
Yes or No
Justification
1. 𝑦 = 𝑥2 + 2
2. 𝑦 = 2𝑥 − 10
3. 𝑦 = 9 − 2𝑥2
4. 𝑦 = 2𝑥
+ 2
5. 𝑦 = 3𝑥2 + 𝑥3 + 2

7. Seat Work
II. Find the second differences in y then write Q on the blank if the given table of
values show quadratic function, NQ if not.
____1.
____2.
X -2 -1 0 1 2
Y 4 1 0 1 4
X -2 -1 0 1 2
Y -1 -2 -1 2 7