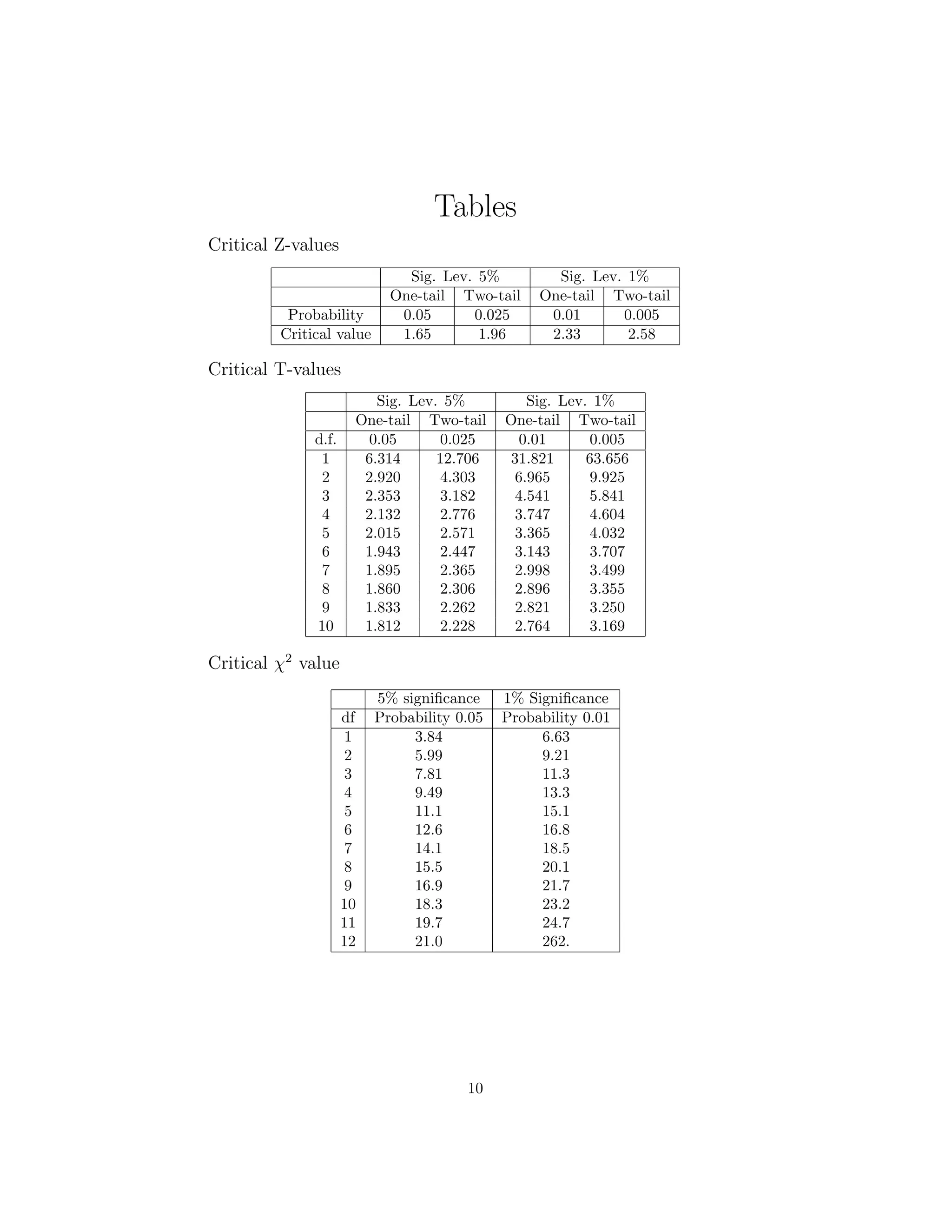
1. The document provides worked solutions to mathematical problems involving differentiation, graph sketching, solving quadratic equations, and probability. 2. A key is provided with common statistical formulas and tables for critical values of t and z distributions. 3. The problems cover a range of mathematical topics at an intermediate level, with multiple parts requiring setting up and solving equations as well as interpreting results.

1. Subtract 1
2 mark for improper fraction or incorrect rounding.
Question marks: 5, 8, 14, 6, 11, 10, 16, 15, 8, 7
1. (a) Evaluate y2
x−1
+ 2x when y = 2 and x = 4. (2 marks)
(22
× 4−1
) + 2 × 4 = 9
1 mark for working, 1 mark for answer.
(b) Simplify (x
3/2
÷ x3
)4
. (3 marks)
(x
3/2
÷ x3
)4
= (x
3/2−3
)4
= (x
− 3/2
)4
= x−6
1 mark for working, 2 marks for solution.
2. (a) What is the equation of the line passing through the points (1, 7)
and (−1.5, −3)? (4 marks)
m = 7−(−3)
1−(−1.5) = 4 1 mark
7 = 4 × 1 + c 1 mark
c = 3 1 mark
y = 4x + 3 1 mark
(b) Solve the simultaneous equations (4 marks)
x + y = −2
12x − 3y = −9
3 × eqn1: 3x + 3y = −6 2 marks for cancelling or substitution
eqn2 + 3 × eqn1: 15x = −15
x = −1 1 mark
−1 + y = −2
y = −1 1 mark
3. (a) Differentiate y = −3x2
+ 2x + 1. (2 marks)
dy
dx = −6x + 2
(b) What are the x and y co-ordinates of the stationary point of the
graph
y = −3x2
+ 2x + 1? (3 marks)
−6x + 2 = 0 1 mark
x = 1/3 1 mark
y = −3 × (1/3)2
+ 2 × (1/3) + 1 = 4/3 1 mark
(c) What is the nature of this stationary point? (2 marks)
d2
y
dx2 = −6 1 mark
−6 < 0 Stationary point is a maximum 1 mark
OR a well reasoned argument involving the shape of x2
and the
negative coefficient.
1

2. (d) Sketch the graph y = −3x2
+ 2x + 1 making sure to label your
sketch clearly. (5 marks)
0.33−0.33 1
1
1.33
x
y
1 mark for each of (−1/3, 0), (1, 0), (0, 1), (0.33, 1.33), 1 mark for
shape.
(e) On different axes sketch the graph y = −3x2
+ 2x − 5. Make sure
to label your sketch clearly. (2 marks)
0.33−5
x
y
1 mark for (0, −5), 1 mark for shape
4. A railway driver notes the number of minutes late his train is over a period
of 13 days.
1 3 2 -1 7 -6 1 1 5 5 4 0 7
(a) What is the mode? (1 marks)
The most common value is 1.
2

3. (b) What is the median? (2 marks)
The ordered data is
-6 -1 0 1 1 1 2 3 4 5 5 7 7
1 mark for table.
13 × 1/2 = 6.5
median is 7th term 2 1 mark for answer.
(c) What is the interquartile range? (3 marks)
13 × 1/4 = 3.25 1
2 mark
Q1 is the 4th term =1 1
2 mark
13 × 3/4 = 9.75 1
2 mark
Q3 is the 10th term =5 1
2 mark
IQ = Q3 − Q1 = 5 − 1 = 4 1 mark
5. Solve the following quadratic equations using the method stated. No
points will be awarded if another method is used. Leave answers
in surd form.
(a) 3x2
− 2x − 2 = 0. Solve by completing the square. (5 marks)
Divide by 3:
x2
− 2
3 x − 2
3 = 0
(x − 1
3 )2
− 1
9 − 2
3 = 0 2 marks
(x − 1
3 )2
= 7
9 1 mark
x − 1
3 = ±
√
7
3 1 mark
x = 1
3 ±
√
7
3 1 mark
(b) −2x2
+ 5x − 1 = 0. Solve by using the quadratic formula. (4
marks)
a = −2, b = 5, c = −1 1 mark for identifying a, b, c
x =
−5±
√
52−4×(−2)×(−1)
2×−2 1 mark
x = 5±
√
17
4 2 marks
(c) x2
+ 4x − 5 = 0. Solve by factorising. (2 marks)
(x + 5)(x − 1) = 0 1 mark
x = −5, x = 1 1 mark
6. (a) Show that there is a solution to x3
− 4x2
− 2x + 1 = 0 for some x
between 0 and 1. (3 marks)
f(x) = x3
− 4x2
− 2x + 1
f(0) = 03
− 4 × 02
− 2 × 0 + 1 = 1 > 0 1 mark
f(1) = 13
− 4 × 12
− 2 × 1 + 1 = −4 < 0 1 mark
f(0) > 0, f(1) < 0 so there is a solution between 0 and 1. 1 mark
3

4. (b) Use the iteration formula xn+1 = −1
x2
n−4xn−2 to find a solution to
2 d.p. (7 marks)
x0 = 0.5
x1 = 0.27
x2 = 0.33
x3 = 0.31
x4 = 0.32
x5 = 0.32
Solution is 0.32 to 2d.p.
1 mark for choice of x0, 4 marks for working, 1 mark for stopping
at a reasonable stage, 1 mark for solution.
7. A food journalist wants to find out if there is a relationship between where
people live and what their favourite food is. She asks 80 people from
around Britain and gets the following data.
England Wales Scotland Ireland
Pizza 1 4 8 6
Curry 8 10 22 4
Fish and Chips 11 4 1 1
(a) State the null hypothesis and the alternative hypothesis. (2
marks)
H0 : There is no correlation. 1 mark
H1 : There is a correlation. 1 mark
(b) What is the χ2
test statistic? (10 marks)
The totals are
England Wales Scotland Ireland Row total
Pizza 1 4 8 6 19
Curry 8 10 22 4 44
Fish and Chips 11 4 1 1 17
Column total 20 18 31 11 80
The fit table is
4.75 4.275 7.3625 2.6125
11 9.9 17.05 6.05
4.25 3.825 6.5875 2.3375
The residual table is
-3.75 -0.275 0.6375 3.3875
-3 0.1 4.95 -2.05
6.75 0.175 -5.5875 -1.3375
The χ2
table is
4

5. 2.9605 0.0177 0.0552 4.3924
0.8182 0.0010 1.4371 0.6946
10.7206 0.0080 4.7393 0.7653
The test statistic is 26.6.
2 marks per table (-0.5 per error), 2 marks for solution.
(c) If we test at a 1% level of significance what is the critical χ2
value?
(2 marks)
Degree of freedom is (4 − 1) × (3 − 1) = 6 1 mark
Critical value is 16.8 1 mark
(d) What can we deduce? (2 mark)
26.8 > 16.8 so there is a correlation between the food people
prefer and the country they live in.
8. A Baker claims there is a mean of 17 cherries in each of his cherry cakes.
A customer buys 9 random cherry cakes and notes how many cherries are
in each one. He writes his test data in a table.
10 15 19 16 1 20 13 15 17
(a) State the null hypothesis and the alternative hypothesis. (2
marks)
H0 : µ = 17 1 mark
H1; µ = 17 1 mark
(b) What is the mean of the test data? (2 marks)
µ(X) = 10 + 15 + 19 + 16 + 1 + 20 + 13 + 15 + 17/9 = 126/9 = 14
1 mark for method, 1 mark for solution.
(c) What is the sample standard deviation of the test data? (4
marks)
(X[i])2
= 100 225 361 256 1 400 169 225 289
σ2
(X) = 100+225+361+256+1+400+169+225+289−9×142
9−1 = 2026−1764
8 =
32.75
σ(X) = 5.723 to 3 d.p. 1 mark for square values, 1 mark for
working, 2 marks for solution.
(d) What is the T test statistic? (3 marks)
µ = 17, µ(X) = 14, σ(X) = 5.723, n = 9.
T = 14−17
5.723/
√
9
= −1.57 to 2 d.p. 1 mark for identifying variables, 1
mark for working, 1 mark for answer.
5

6. (e) The study is taken with a 1% level of significance. What is the
critical T value? (2 marks)
D.f. = 9 − 1 = 8 1 mark
1%, two tailed
Critical values are -3.355 and 3.355. 1 mark
(f) What can we deduce? (2 marks)
−3.355 < −1.57 so we accept the null hypothesis.
9. Consider the following shape.
4
a
60
80
40 b
(a) What is the length a to 2 d.p.? (2 mark)
tan(60) = a
4
a = 4 tan(60) = 4
√
3 = 6.93.
1 mark for working, 1 mark for solution.
(b) What is the area of the above shape to 1 d.p.? (6 marks)
The area of the left triangle is 0.5 × 4
√
3 × 4 = 8
√
3. 2 marks
The third angle in the right triangle is 180 − 80 − 40 = 60. 1
mark
b
sin(60) = 4
√
3
sin(80)
b = 6.09. 1 mark
The area of the right triangle is 0.5×6.09×4
√
3×sin(40) = 13.57
to 2d.p. 1 mark
Total area is 13.57 + 8
√
3 = 27.4 to 1 d.p. 1 mark
6

7. 10. A lady has one 2 pound coin, three 1 pound coins and six 10p coins coins
in her purse. She is considering buying a muffin costing 1.10 and a coffee
costing 80p.
(a) What is the probability that after pulling out 1 coin the lady will
have enough money for the coffee? (1 mark)
P(1) + P(2) = 1/10 + 3/10 = 2/5 1 mark for solution.
(b) What is the probability that after pulling out 2 coins the lady will
have the exact money for the muffin? (2 marks)
Combinations are 1 then a 10p or 10p then 1. P(1, 10p) +
P(10p, 1) = 3/10 × 6/9 + 6/10 × 3/9 = 2/5
1 mark for working, 1 mark for solution.
(c) What is the probability that after pulling out 2 coins the lady will
have enough money for the coffee and the muffin? (4 marks)
Combination of coins 2,1; 2,10p; 1,1. Probability is
2×1/10×3/9+2×1/10×6/9+3/10×2/9 = 4/15 1 mark per probability
and 1 mark for solution.
7

8. Formulae
Let X be a list of data of size n.
Mean:
µ(X) =
n
i=1 X[i]
n
Variance
σ2
(X) =
n
i=1(X[i])2
n
− µ2
(X)
Z-statistic
Z =
µ(X) − µ
σ/
√
n
Sample Variance
σ2
(X) =
n
i=1(X[i])2
− nµ2
(X)
n − 1
T-statistic
T =
µ(X) − µ
σ(X)/
√
n
Alternative notation
Mean
¯x =
x
n
Variance
V ar =
x2
n
− ¯x2
Z-statistic
Z =
¯x − A
σ/
√
n
Sample Variance
s2
=
x2
− n¯x2
n − 1
T-statistic
T =
¯x − A
s/
√
n
8

9. Pythagoras’ Theorem
a2
+ b2
= c2
tan(A) =
opp
adj
, cos(A) =
adj
hyp
, sin(A) =
opp
hyp
Sine rule
a
sin(A)
=
b
sin(B)
=
c
sin(C)
Cosine rule
a2
= b2
+ c2
− 2bc cos(A)
Area
Area = 1/2ab sin(C)
Quadratic formula
x =
−b ±
√
b2 − 4ac
2a
Equation of a straight line
y = mx + c
Gradient of a straight line
m =
y2 − y1
x2 − x1
9

10. Tables
Critical Z-values
Sig. Lev. 5% Sig. Lev. 1%
One-tail Two-tail One-tail Two-tail
Probability 0.05 0.025 0.01 0.005
Critical value 1.65 1.96 2.33 2.58
Critical T-values
Sig. Lev. 5% Sig. Lev. 1%
One-tail Two-tail One-tail Two-tail
d.f. 0.05 0.025 0.01 0.005
1 6.314 12.706 31.821 63.656
2 2.920 4.303 6.965 9.925
3 2.353 3.182 4.541 5.841
4 2.132 2.776 3.747 4.604
5 2.015 2.571 3.365 4.032
6 1.943 2.447 3.143 3.707
7 1.895 2.365 2.998 3.499
8 1.860 2.306 2.896 3.355
9 1.833 2.262 2.821 3.250
10 1.812 2.228 2.764 3.169
Critical χ2
value
5% significance 1% Significance
df Probability 0.05 Probability 0.01
1 3.84 6.63
2 5.99 9.21
3 7.81 11.3
4 9.49 13.3
5 11.1 15.1
6 12.6 16.8
7 14.1 18.5
8 15.5 20.1
9 16.9 21.7
10 18.3 23.2
11 19.7 24.7
12 21.0 262.
10