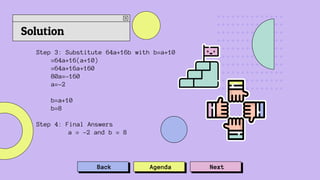
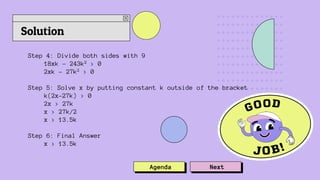
The document discusses solving polynomial equations and modulus functions. It provides a specific example with a polynomial defined by constants a and b and outlines the steps taken to find their values, concluding that a = -2 and b = 8. Additionally, it addresses solving an inequality involving a modulus function and provides the final solution as x > 13.5k.