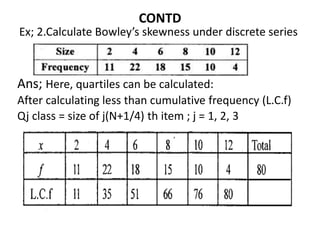
This document discusses Bowley's coefficient of skewness, which is a measure of the skewness of a data distribution based on the positions of the quartiles. It provides examples of calculating Bowley's skewness for individual and discrete data series by finding the first quartile, third quartile, and median. The document also includes multiple choice questions to test understanding of measures of skewness, Karl Pearson's coefficient of skewness, and Bowley's coefficient of skewness.

1. PROGRAMME B.COM
SUBJECT
QUANTITATIVE TECHNIQUE – I
SEMESTER III
UNIVERSITY VIJAYANAGAR SRI
KRISHNADEVARAYA UNIVERSITY,
BALLARI
SESSION 54

2. RECAP
• Karl Pearson's Co-efficient of Skewness Under
Continuous Series Problems---------02

3. LEARNING OBJECTIVES
• The aim of the chapter is to make students to
understand Measures of Skewness, Karl Pearson
Co-efficient of Skewness and Bowley's Co-efficient
of skewness

4. LEARNING OUTCOMES
• After this Unit The Students can be able to apply to
Sample Population Data by Differentiating Normal
and Abnormal Distributions with regard to
Dispersion & Skewness.

5. SESSION - 54
• Bowely's Co-efficient of Skewness Under Individual
and Discrete Series Problems----------------02

6. Bowley’s Co-efficient of Skewness
In Karl Pearson method of measuring skewness the
whole of the series is needed. Prof. Bowley has
suggested a formula based on position of quartiles. In
symmetric distribution quartiles will be equidistance
from the median. Q2 – Q1 = Q3 – Q2 , but in skewed
distributions it may not happen. Hence
Q3 + Q1 – 2Median OR Q2
SK = Q3 – Q1

7. CONTD
Ex ; 1. Calculate Bowley’s skewness under individual
series; 10,15,20,25,30,35,40,
Calculation of Bowely’s skewness
10,15,20,25,30,35,40, N = 7
Q1= size of (N+1/4) = (7+1/4) = 8/4= 2nd item, Q1 = 15
Q3 = size of 3(N+1/4) = 3(7+1/4) = 3(8)/4 = 24/4
Q3 = 24/4 , 6th item Q3 = 35
Median = size of N+1/2 = 7+1/2= 8/2 = 4th item
Median = 25
Q3 + Q1 – 2Median OR Q2
SK = Q3 – Q1 = 35 + 15 – 2x25
35 - 15
SK = 00

8. CONTD
Ex; 2.Calculate Bowley’s skewness under discrete series
Ans; Here, quartiles can be calculated:
After calculating less than cumulative frequency (L.C.f)
Qj class = size of j(N+1/4) th item ; j = 1, 2, 3

9. CONTD
Q3 +Q1 – 2Median
SK = Q3 – Q1 OR

10. SUMMARY
As we already discussed and learnt today on skewness
as below
Bowely's Co-efficient of Skewness Under Individual and
Discrete Series Problems----------------02

11. MCQs
1 .The distribution in sum of Q3+Q1= 44,Q3–Q1= 16 and
median = 21, bowley skewness
a) 0.125
b) Positive skewed
c) Negative skewed
d) None of these
2. formula of Bowley’s of skewness
a) Sk= Q3+ Q1 – 2median/ Q3 – Q1
b) Negatively skewed
c) Symmetrical
d) None of these

12. MCQs
3 . If mean = 36.31 and Mode = 32 and S.D =15.8 then
Karl Pearson co efficient of skewness is
a) 0.27
b) Different
c) Zero
d) None of these
4. If mean = 36.31 and Mode = 32 and Karl Pearson co
efficient of skewness is 0 .27, S.D =?
a) Positive Skewed
b) Negative Skewed
c) 15.8
d) None of these

13. MCQs
5 . The values of mean, median and mode can be
a) Some time equal
b) Never equal
c) Always equal
d) None of these

14. CONTD
ANSWERS
1. A
2. A
3. A
4. C
5. A

15. REFERENCES
• S.P. Gupta, Sultan Chand and Sons Publications, 2017
• S. C. Gupta, Himalaya Publishing House,
Fundamentals of Statistics, 2018
• R.S.N Pillai and Bagavathi, S.Chand publications, 2010

16. THANK YOU