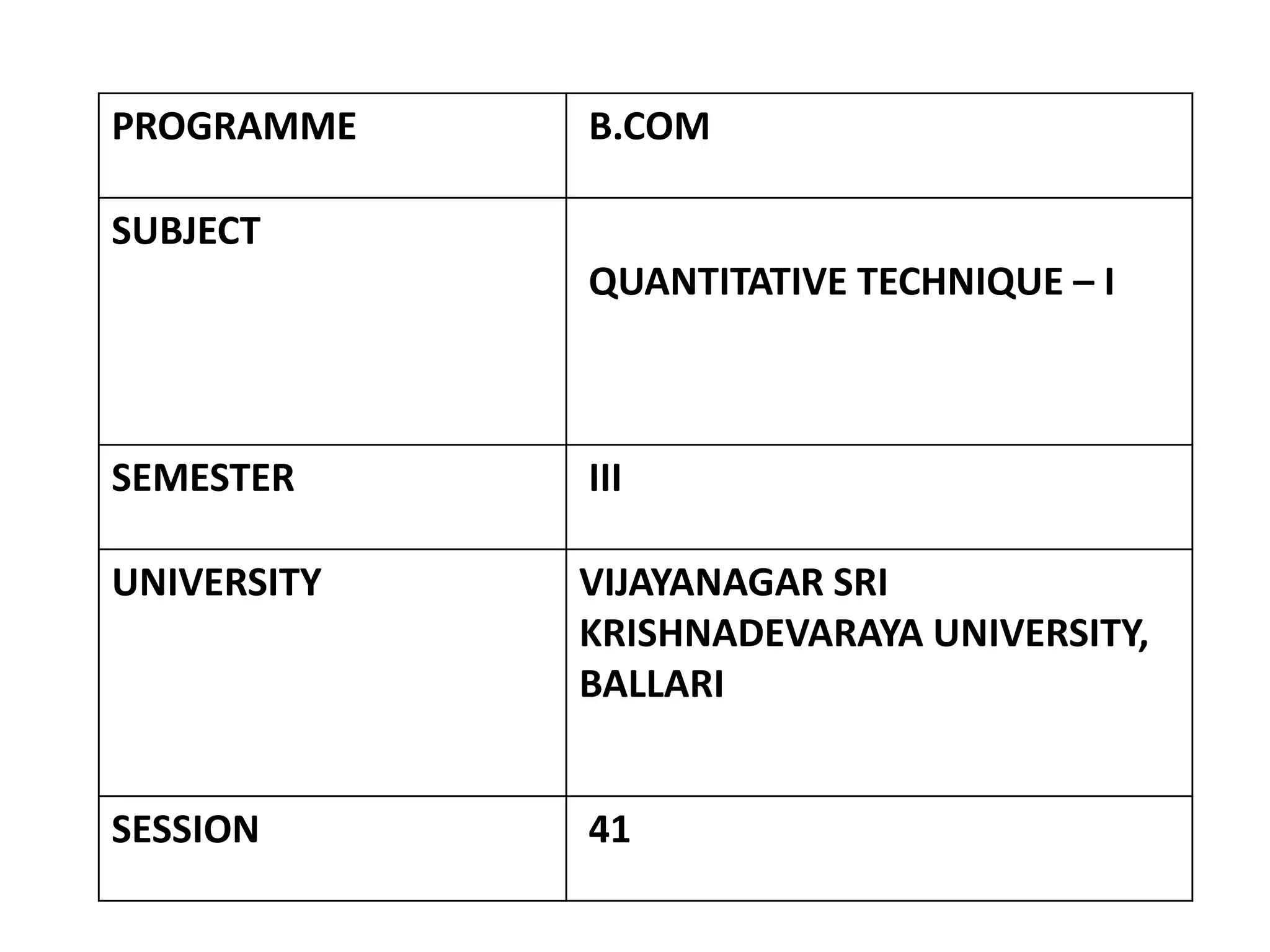
This document discusses quantitative techniques as part of a B.Com program. It covers measures of central tendency and dispersion, including the mean, median, mode, range, mean deviation, and standard deviation. The learning objectives are to understand different measures of central tendency and dispersion. The learning outcomes are to differentiate, determine, and identify relationships between averages, and apply measures of dispersion to data by comparing standard deviation to mean deviation. The document also provides examples and practice questions on these topics.

1. PROGRAMME B.COM
SUBJECT
QUANTITATIVE TECHNIQUE – I
SEMESTER III
UNIVERSITY VIJAYANAGAR SRI
KRISHNADEVARAYA UNIVERSITY,
BALLARI
SESSION 41

2. RECAP
• Merits & Demerits of Mean, Median and Mode

3. LEARNING OBJECTIVES
• After reading this chapter, a student will be
understand different measures of central tendency
and Dispersion, i.e., Arithmetic Mean,Mean,Mode,
Geometric and Harmonic mean & Range, Mean
Deviation, Standard Deviation, Quartile Deviation,
Co efficient of variation

4. LEARNING OUTCOMES
• After the Chapter, The Students Shall be able to
Differentiate, Determine, and Identify the
relationships among Averages under Different
Series of Data and too State the Merits and
Demerits of Three Measures. The Students will
apply Measures of Dispersion to Sample Population
Data by Contrasting the Values of Standard
Deviation & The Mean Deviation, Synthesizing the
Mean,Standard,and Quartile Deviations into a
Useful Description of a Set of Data

5. SESSION - 41
• Measures of Dispersion, Meaning, Definition,
Concept, Purposes and Methods

6. Meaning and Concept of dispersion
Dispersion is the extent to which values in a distribution
differ from the average of the distribution.
Or dispersion helps to understand the distribution of
the data.
Concept
A measure of dispersion indicates the scattering of
data. It explains the disparity of data from one another,
delivering a precise view of their distribution. The
measure of dispersion displays and gives us an idea
about the variation and the central value of an
individual item

7. Definition and Purposes of Dispersion
MEANING
A.L Bowley defines dispersion is the measure of the
variation of the items.
Purposes of Dispersion
(1) Comparative study
(2) Reliability of an average
(3) Control the variability
(4) Basis for further statistical analysis

8. Types of Dispersion
I. Absolute Measure of Dispersion
• Range
• Quartile deviation
• Standard deviation
• Mean deviation
II. Relative Measure of Dispersion
• Co-efficient of Range
• Co-efficient of Variation
• Co-efficient of Standard Deviation
• Co-efficient of Quartile Deviation
• Co-efficient of Mean Deviation

9. MCQs
I. The scatter in a series of values about the average is
called:
(a) Central tendency
(b) Dispersion
(c) Skewness
(d) Symmetry
II. The measurements of spread or scatter of the
individual values around the central point is called:
(a) Measures of dispersion
(b) Measures of central tendency
(c) Measures of skewness
(d) Measures of kurtosis

10. MCQs
III. The measures used to calculate the variation present
among the observations in the unit of the variable is
called:
(a) Relative measures of dispersion
(b) Coefficient of skewness
(c) Absolute measures of dispersion
(d) Coefficient of variation
IV. The degree to which numerical data tend to spread
about an average value called:
(a) Constant
(b) Flatness
(c) Variation
(d) Skewness

11. MCQs
V. The measures used to calculate the variation present
among the observations relative to their average is
called:
(a) Coefficient of kurtosis
(b) Absolute measures of dispersion
(c) Quartile deviation
(d) Relative measures of dispersion

12. CONTD
ANSWERS
I. B
II. A
III. C
IV. C
V. D

13. REFERENCES
• S.P. Gupta, Sultan Chand and Sons Publications, 2017
• S. C. Gupta, Himalaya Publishing House,
Fundamentals of Statistics, 2018
• R.S.N Pillai and Bagavathi, S.Chand publications, 2010

14. THANK YOU