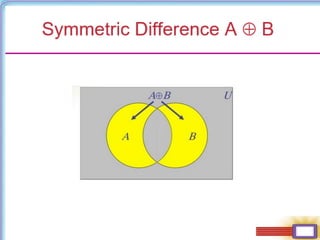
The document discusses binary operations on sets. It provides examples of multiplication and addition operations on the set of integers Z. It introduces the concept of a Cayley table to represent a binary operation on a finite set using a table. The identity element and inverses are discussed. It is noted that the inverse of an element, if it exists, is unique. Examples are provided to check if binary operations are closed, commutative, associative, and have identities and inverses.

1. Binary Operations
2021

2. Binary Operations
Take the multiplication
operation on the set of integers,
Z = {0, ±1, ±2, ±3,…}:
x = +3 and y = +4
x × y = +12
(x, y) ∈ Z × Z and x × y ∈ Z
We write *: Z × Z → Z; (x, y) → x × y

3. Binary Operations
Take the addition operation
on the set of integers, Z =
{0, ±1, ±2, ±3,…}:
x = +3 and y = -4
x + y = +3 + (-4) = -1∈ Z
(x, y) ∈ Z × Z and x + y ∈ Z
We write *: Z × Z → Z; (x, y) → x + y

4. Binary Operation:
: (x, y ) → f(x, y)
That is a calculation that combines two elements
of the set (called operands) to produce another
element of the set. It maps elements of the
Cartesian product A × A into A itself. i.e. f: A × A
→ A. We call the operation multiplication!

5. Binary Operation notation
• We usually write binary operations
infix that is, between their arguments,
rather than prefix, before their
arguments.
• Also, the symbols chosen for binary
operations are usually reminiscent of
+ or × rather than letters.

6. Examples: Infix notation
Note the infix positioning of the operation
characteristic of binary operations.

7. Binary operations on Z
Given the set of integers X, we normally call the
operation “multiplication” and denote it by * even
though we can define the operations in many ways:
• x * y = x + 2y + 3
• x * y = 1 + xy
• x * y = 3x + y
or even
• x * y = x + y

8. Binary Operation Examples

9. Binary Operations Examples

10. Binary Operations Examples

11. Are these binary operations?
1. a * b = a + b – 1
2. a * b = 1 – 2ab
3. a * b = a/b
4. a * b = a/b on Z {0}
5. For a, b ∈ A, a * b = a + b where A is the set A
= {1, 2, 3, 4}.
Given a, b ∈ Z. Consider the operations *: Z × Z → Z
as follows:

12. Example: Closure

13. Some interesting questions?
• Commutativity: does the order in which we
perform the operation matter?
• Associativity: does it matter how we group the
operands?
• Identity: is there are element which when used
as an operand with another object returns the
same object?

14. Binary
Operati
on
Definitions:

15. Addition: +: R × R → R; (x, y) → x + y

16. Multiplication:*: R × R → R; (x, y)→ x × y

17. Multiplication:*: R × R → R; (x, y)→ x × y

18. Subtraction: *: R × R → R; (x, y) → x - y

19. Subtraction: *: R × R → R; (x, y) → x - y

20. Division: *: R{0} × R{0} → R{0}; (x, y) → x / y

21. Division: *: R{0} × R{0} → R{0}; (x, y) → x / y

22. Define an identity element for a binary operation.

23. Binary
Operati
on
Identity Element

24. RTP: The Identity Element is Unique

25. The identity element e of a binary
operation  is unique.
Suppose that e and e’ are two
identities of *.
Then, e * e’ = e since e’ is an
identity and also e * e’ = e’ since e
is an identity and hence e = e’ and
the identities are unique. ■

26. Identity Element

27. Is there an identity element for
this binary operation?
• Let * be the binary operation on S
= {1, -1, i, -i} with i2 = -1 defined
by a * b = a x b.
• Is there an identity element for *?
* 1 -1 i -i
1 1 -1 i -i
-1 -1 1 -i i
i i -i -1 1
-i -i i 1 -1

28. Binary
Operati
on
Identity Element
• For the set Z, the integer 1 is an identity w. r. t.
“”, but not w. r. t. “+”.
• The number 0 is an identity w. r. t. “+”.

29. Binary
Operati
on
Identity Element
Let “” be the operation defined on Z, x  y = x +
y  1. Then is there an identity?

30. Identity Element

31. Let “∆” be the operation defined on Z, x ∆ y = 1 + xy.
Then the operation has no identity element in Z
Hint: Assume there is an identity element e, then
x ∆ e = 1 + xe = x
What does that give us?

32. SOLUTION
Let “∆” be the operation defined on Z, x ∆ y = 1 + xy.
Then the operation has no identity element in Z.
SOLUTION
Assume there is an identity element e, then
x ∆ e = 1 + xe = x
⇒ xe = x - 1
⇒ e = (x – 1)/x = 1 - 1/x ∉ Z

33. A binary operation which is NOT commutative?

34. A binary operation which is NOT associative?

35. Explanation

37. Using a table to represent a Binary operation
• Consider the set A = {-1, 1} under the usual
multiplication as we know it. We can think of x, and y
as the elements of this set. Let us compute all the
products for the elements of this set.
• This produces the results:
1 * 1 = 1 × 1 = 1
1 * -1 = 1 × -1 = -1
-1 * 1 = -1 × 1 = -1
-1 * -1 = -1 × -1 = 1

38. Summarising, in a table we have…
• Consider the set A = {-1, 1} under the usual
multiplication as we know it. We can think of x, and y
as the elements of this set. Let us compute all the
products for the elements of this set.
• This produces the results:
1 * 1 = 1 × 1 = 1
1 * -1 = 1 × -1 = -1
-1 * 1 = -1 × 1 = -1
-1 * -1 = -1 × -1 = 1
* 1 -1
1 1 -1
-1 -1 1

39. Cayley Table
When we are given a binary
operation on a finite set, it is common
to specify it in tabular form,
sometimes called a Cayley table.

40. Arthur Cayley
Born: 16 Aug 1821 Died: 26 Jan 1895

41. • In 1863 Cayley was appointed Sadleirian
professor of Pure Mathematics at Cambridge.
• He published over 900 papers and notes
covering nearly every aspect of modern
mathematics.
Arthur Cayley

42. The most important of his work was
developing the algebra of matrices, work in
non-Euclidean geometry and n-dimensional
geometry.
As early as 1849 Cayley wrote a paper
linking his ideas on permutations with
Cauchy's.
 In 1854 Cayley wrote two papers which are
remarkable for the insight they have of
abstract groups.
Arthur Cayley

43. At that time the only known groups were
permutation groups and even this was a
radically new area, yet Cayley defines an
abstract group and gives a table to display the
group multiplication.
These tables become known as Cayley Tables.
Arthur Cayley

44. He gives the 'Cayley tables' of some special
permutation groups but, much more
significantly for the introduction of the
abstract group concept, he realised that
matrices were groups .
Arthur Cayley

45. Cayley Table
• Take * to be the binary
operation on S = {1, -1, i, -
i} with i2 = -1 defined by a *
b = a × b the corresponding
Cayley table is:
• Here is another example of a Cayley table.
* 1 -1 i -i
1 1 -1 i -i
-1 -1 1 -i i
i i -i -1 1
-i -i i 1 -1

46. Let “” be the operation defined as x  y = x + y  1 on
Z, show that “” is both commutative and associative.

47. SOLUTION
Let “” be the operation defined as x  y = x + y  1 on Z,
then “” is both commutative and associative.
Proof: Commutative:
x * y = x + y – 1 = y + x – 1 = y * x
Associative:
x * (y * z) = x * (y + z – 1)
= x + (y + z – 1) -1
= (x + y – 1) * z = (x * y) * z
Thus, * is both commutative and associative on Z.

48. Let *: Z × Z → Z; (x, y) →1 + xy. Show
that * is commutative but not associative.

49. Show: x  y = x + 2y. This operation is neither
commutative, nor associative.

50. Show: x  y = x + 2y. This operation is neither
commutative, nor associative.
• Commutative:
x * y = x + 2y ≠ y + 2x = y * x
So, it is not commutative.
• Associative:
x * (y * z) = x * (y + 2z)
= x + 2(y + 2z) = x + 2y + 4z
(x * y) * z = (x + 2y) * z = x + 2y + 2z
So, * is not associative

51. Consider the Binary Operation * as given by…
Find the answer to:
1) a * (b * c)
2) (a * b) * c
3) a * (b * (c * d))

52. Consider the Binary Operation * as given by…
On what set is the operation *
defined?
Is the operation * closed?
Is there an element e such
that a * e = a = e * a?

53. Inverses

54. Inverses
• Is this a binary operation?
• Is there an identity element?
• Is there an element x-1 such
that for every x we have x *
x-1 = e = x-1 * x?

55. Let * be an associative binary operation on a set A with identity
e. If x has an inverse, show that this inverse is unique.
Let y and z be inverses of x then
Hence y = z.
Thus, if x has an inverse, that inverse is unique.

56. Let * be an associative binary operation on a set A with identity
e. If x has an inverse, show that this inverse is unique.
Let y and z be inverses of x then
y = y * e By the property of identity
= y * (x * z) Since z is an inverse of x
= (y * x) * z Since * is associative
= e * z Since y is an inverse of x
= z By the property of identity
Hence y = z.
Thus, if x has an inverse, that inverse is unique.

57. Inverses

58. 2 x 2 Matrices with real coefficients
under component wise addition
Consider the set of 2 x 2 matrices with real
coefficients under component wise addition…
• Is this a binary operation?
• Is the operation commutative and associative?
• What is the identity for the operation?
• Do the elements have inverses?

59. 2 x 2 Matrices with real coefficients
under component wise addition
Consider the set of 2 x 2 matrices with real
coefficients under component wise addition…

60. Do inverses exist?
• Consider the set of 2 x 2 matrices over the field
of real numbers. Is multiplication a binary
operation?
• Is there an identity element?
• Do all 2 x 2 matrices have inverses?

61. Do inverses exist?
• Recall that the inverse of a matrix is A-1 = adj
A/det A. i.e. the matrix of cofactors divided by
the determinant of the matrix.
• For a 2 x 2 matrix to have an inverse, we must
have det A ≠ 0.
• Thus all 2 x 2 matrices do not have inverses
under multiplication.
• Thus, all elements are not invertible.

64. Complex Numbers
• Consider * to be the binary
operation on S = {1, -1, i, -i} with i2
= -1 defined by a * b = a x b.
• The corresponding Cayley table is:
• Is this binary operation closed,
commutative, associative?
• Is there an identity?
• Are there inverses?
* 1 -1 i -i
1 1 -1 i -i
-1 -1 1 -i i
i i -i -1 1
-i -i i 1 -1

65. Is there a way we can check for commutativity
quickly from the Cayley table?…

66. How would you check for associativity?…

67. Closed?

68. Commutative?

69. Associative?

70. Identity element?

71. Example – Power Set
• The intersection and union of two subsets of a set A are
both binary operations on the power set of A, P(A).
• If A = {1, 2} what would be the identity element for
each of these operations?

72. Example – Power Set
• The intersection and union of two subsets of a set A are both
binary operations on the power set of A, P(A).
• If A = {1, 2} what would be the identity element for each of these
operations?
SOLUTION
A= {1, 2} and P(A) = {{}, {1}, {2}, {1, 2}}
• Intersection: ∩: P(A) × P(A) → P(A)
– {1} ∩ {1, 2} = {1} ∈ P(A)

73. Symmetric Difference

75. Symmetric Difference

76. Does this remind us of the Exclusive OR in
propositional logic?

78. Given sets A, B and C. Show that ∆ is associative…
Similarly,

81. Some Past Paper Questions

82. Given a binary operation x  y = x + 2y.This
operation has no identity, thus no inverse.
Try…
x * e =
e * x =
Do you get two different values for the identity?

83. Given a binary operation x  y = x + 2y.This
operation has no identity, thus no inverse.
Consider:
x * e = x + 2e = x ⇒ e = 0
e * x = e + 2x = x ⇒ e = -x
But we know that the identity is unique. Thus, the
operation * has no identity and hence no inverse.

84. Question

85. Question May 2017
a) Commutative:
• 3 * 4 = 3 × 3 + 4 × 4 – 3 × 4 = 25 – 12 = 13
• 4 * 3 = 3 × 4 + 4 × 3 – 4 × 3 = 24 – 12 = 12
So it is not commutative.
b) Identity: If there is an identity e, then n * e = n = e * n ⇒ 3n + 4e – ne = n
then 2n = e(4 – n) and e = 2n/(4 – n). Now for n = 1 e = 2/3 ∉ Z and hence this
operation does not have an identity element. Also 4e + 3n – en = 3e + 4n – ne
So 3n + 4e = 3e + 4n and n = e but the identity is unique so there is no identity.
c) Inverse: Since it does not have an identity, it has no inverses.

86. Past Paper Question

87. Questions