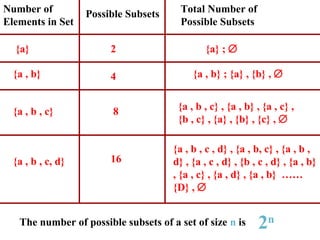
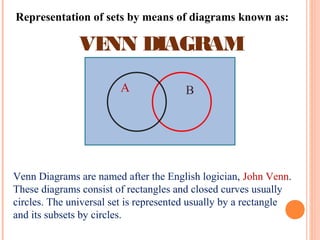
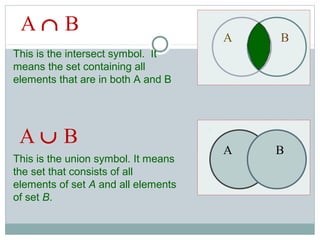
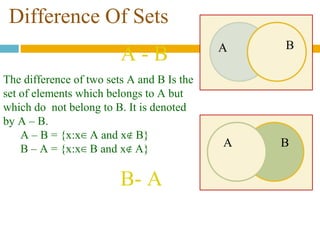
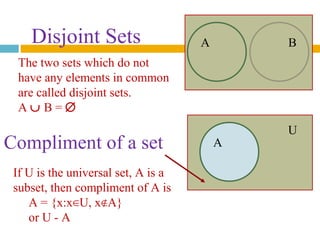
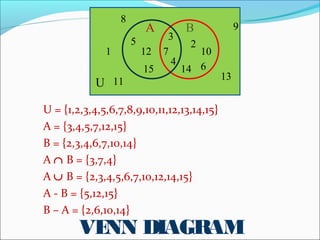
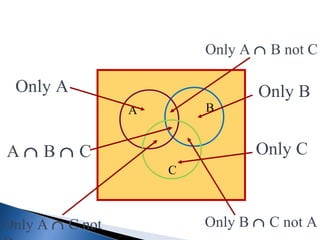
The document defines basic concepts about sets including: - A set is a collection of distinct objects called elements. Sets can be represented using curly brackets or the set builder method. - Common set symbols are defined such as belongs to (∈), is a subset of (⊆), and is not a subset of (⊄). - Types of sets like empty sets, singleton sets, finite sets, and infinite sets are described. - Operations between sets such as union, intersection, difference, and complement are explained using Venn diagrams. - Laws for sets like commutative, associative, distributive, double complement, and De Morgan's laws are listed. - An example problem calculates

1. A = {1, 3, 2, 5}
n(A) = 4
Sets use “curly” brackets
The number of elements
in Set A is 4
Sets are denoted by
Capital letters
A3∈
A7∉
3 is an element of A 7 is not an element of A
SETS
A set is a collection of well defined
distinct objects.
The objects of the set are called elements.

2. {1, 3, 2, 3, 5, 2} We never repeat elements in a set.{1, 2, 3, 5}
Sets can be represented by two
methods:
Rooster or Tabular form:
In this the elements are separated by commas.
e.g. set A of all odd natural numbers less than 10.
A = {1,3,5,7,9}
Set builder method:
In this the common property of the elements is
specified.
e.g. set A of all odd natural numbers less than 10.
A = {x : x is odd natural number less than 10}

3. Symbols Meaning
{ } enclose elements in set
∈ belongs to
⊆ is a subset of (includes equal
sets)
⊂ is a proper subset of
⊄ is not a subset of
⊃ is a superset of

4. Empty set: If a set doesn't contain any elements it is called
the empty set or the null set. It is denoted by ∅ or { }.
Singleton set: It is a set which contains only one element.
e.g. A = {0}
Finite set: It is a set which contains finite number of
different elements.
e.g. A = {a,e,i,o,u}
Infinite set: It is a set which contains infinite number of
different elements.
e.g. A = {x : x ∈ set of natural numbers}
Equal sets: If two or more sets contain the same elements,
they are called equal sets irrespective of the order.
e.g. If A = {1,2,3} and B = {2,3,1}
Then A = B

5. Number of
Elements in Set
Possible Subsets Total Number of
Possible Subsets
{a} {a} ; ∅2
{a , b} {a , b} ; {a} , {b} , ∅4
{a , b , c} {a , b , c} , {a , b} , {a , c} ,
{b , c} , {a} , {b} , {c} , ∅
8
{a , b , c, d}
{a , b , c , d} , {a , b, c} , {a , b ,
d} , {a , c , d} , {b , c , d} , {a , b}
, {a , c} , {a , d} , {a , b} ……
{D} , ∅
The number of possible subsets of a set of size n is 2n
16

6. The Power Set (P)
The power set is the set of all subsets that can be
created from a given set.
Example:
A = {a, b, c}
P (A) = {{a, b}, {a, c}, {b, c}, {a}, {b}, {c}, A, φ}
Cardinal Number of A Set
It is the number of elements in a set.
Example:
A = {a, b, c, d}
n(A) = 4

7. A B
VENN DIAGRAM
Representation of sets by means of diagrams known as:
Venn Diagrams are named after the English logician, John Venn.
These diagrams consist of rectangles and closed curves usually
circles. The universal set is represented usually by a rectangle
and its subsets by circles.

8. A B
A ∩ B
A ∪ B
A B
This is the union symbol. It means
the set that consists of all
elements of set A and all elements
of set B.
This is the intersect symbol. It
means the set containing all
elements that are in both A and B

9. A B
A - B A B
A B
B- A
A B
Difference Of Sets
The difference of two sets A and B Is the
set of elements which belongs to A but
which do not belong to B. It is denoted
by A – B.
A – B = {x:x A and x B}∈ ∉
B – A = {x:x B and x A}∈ ∉

10. A BDisjoint Sets
ACompliment of a set
The two sets which do not
have any elements in common
are called disjoint sets.
A ∪ B = ∅
U
If U is the universal set, A is a
subset, then compliment of A is
A = {x:x U, x A}∈ ∉
or U - A

11. U = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}
A = {3,4,5,7,12,15}
B = {2,3,4,6,7,10,14}
A ∩ B = {3,7,4}
A ∪ B = {2,3,4,5,6,7,10,12,14,15}
A - B = {5,12,15}
B – A = {2,6,10,14}
2
3
4
7
5
6
8
9
10
11
12
13
1415
A B
1
VENN DIAGRAM
U

12. A B
C
A ∩ B ∩ C
Only A Only B
Only C
Only A ∩ B not C
Only B ∩ C not AOnly A ∩ C not

13. Commutative Laws:
A ∩ B = A ∩ B and A ∪ B = B ∪ A
Associative Laws:
(A ∩ B) ∩ C = A ∩ (B ∩ C) and (A ∪ B) ∪ C = A ∪ (B ∪ C)
Distributive Laws:
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) and A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩C)
Double Complement Law:
(Ac
)c
= A
De Morgan’s Laws:
(A ∩ B)c
= Ac
∪ Bc
and(A ∪ B)c
= Ac
∩ Bc

14. 100 people were surveyed. 52 people in a survey owned a cat.
36 people owned a dog. 24 did not own a dog or cat.
universal set is 100 people surveyed
C D
Set C is the cat owners and Set D is the dog
owners. The sets are NOT disjoint. Some
people could own both a dog and a cat.
24
Since 24
did not own
a dog or
cat, there
must be 76
that do own
a cat or a
dog.
52 + 36 = 88 so
there must be
88 - 76 = 12
people that own
both a dog and
a cat.
1240 24
100
Example:

15. THANK YOU