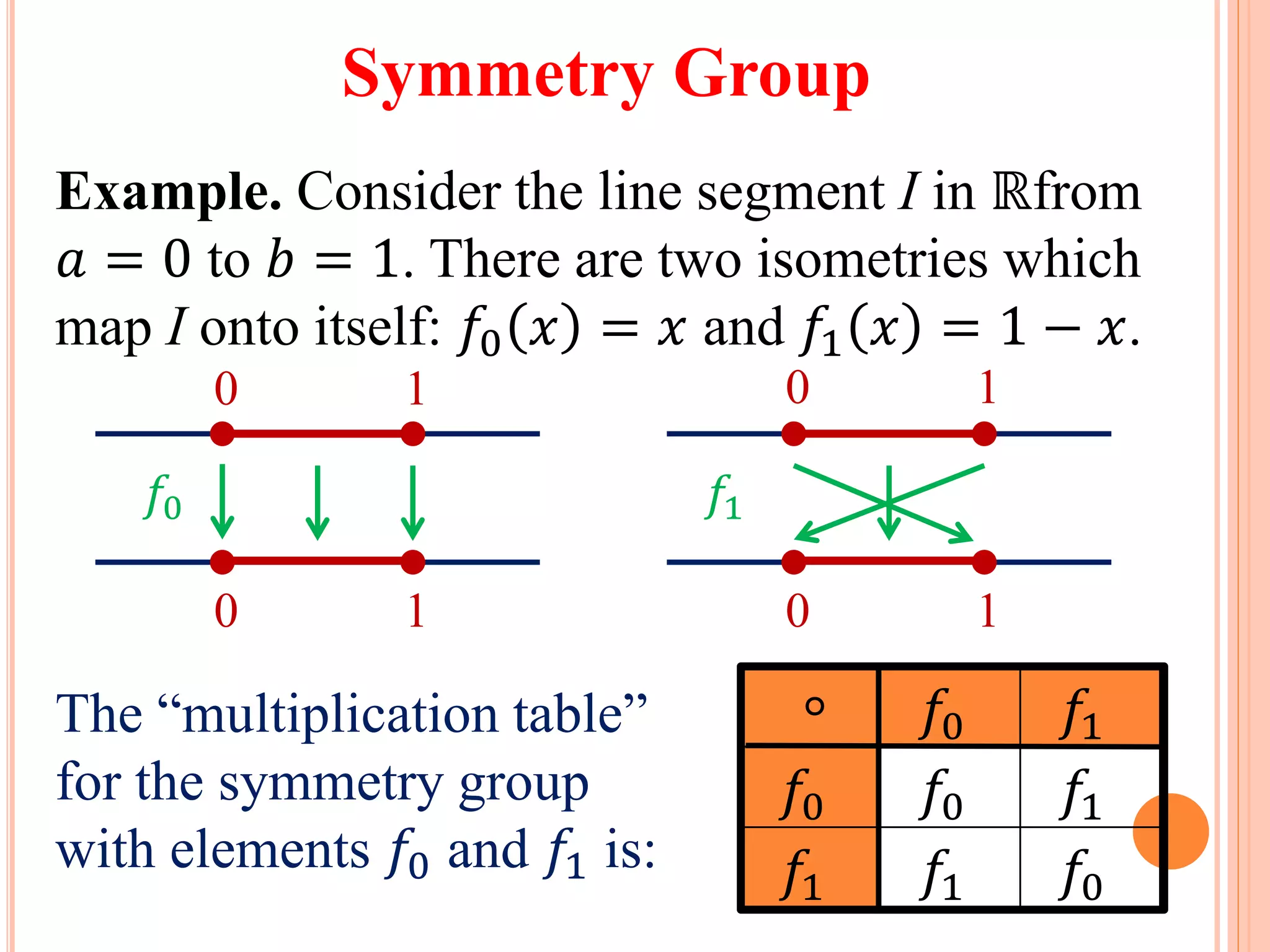
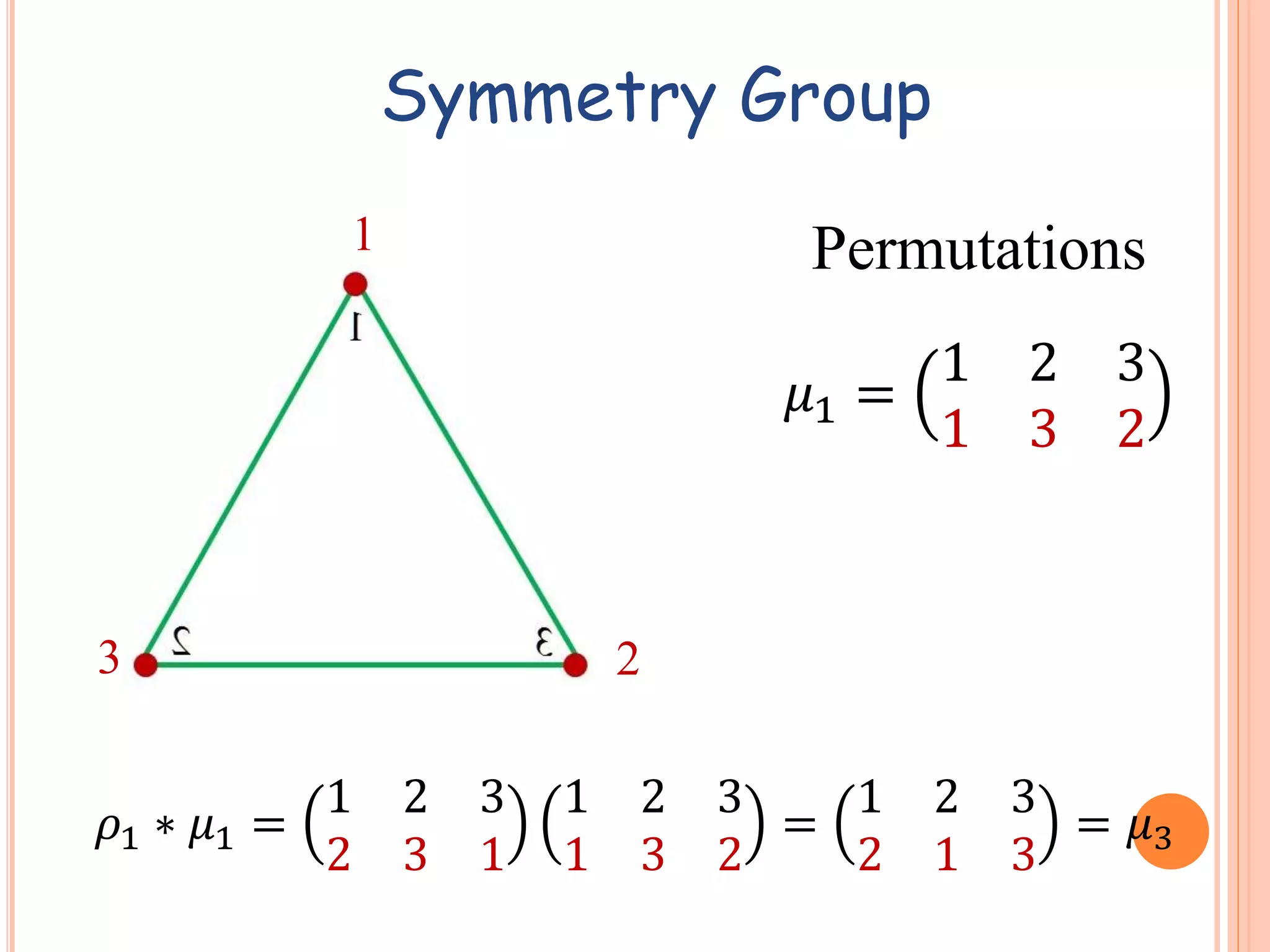
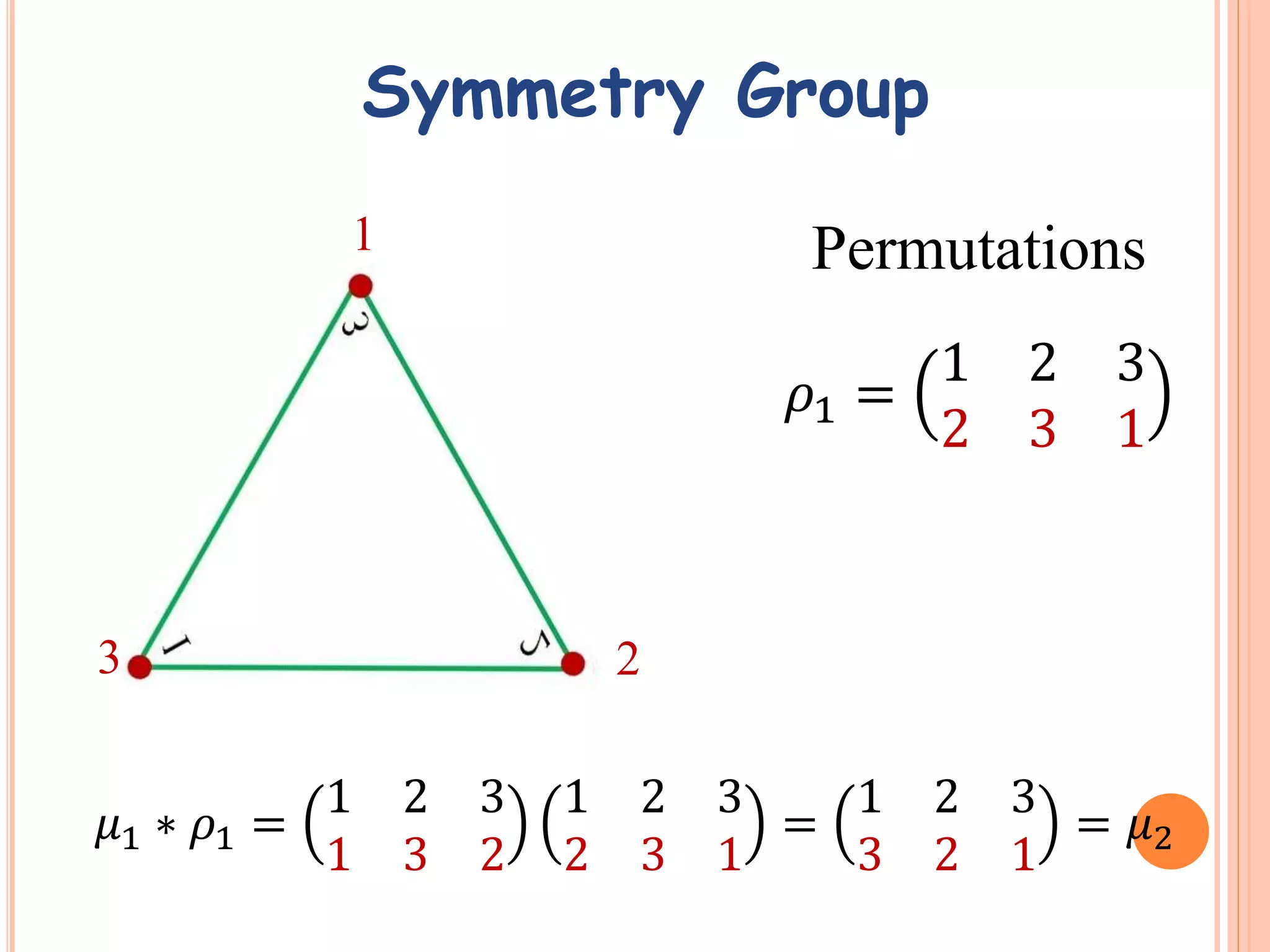
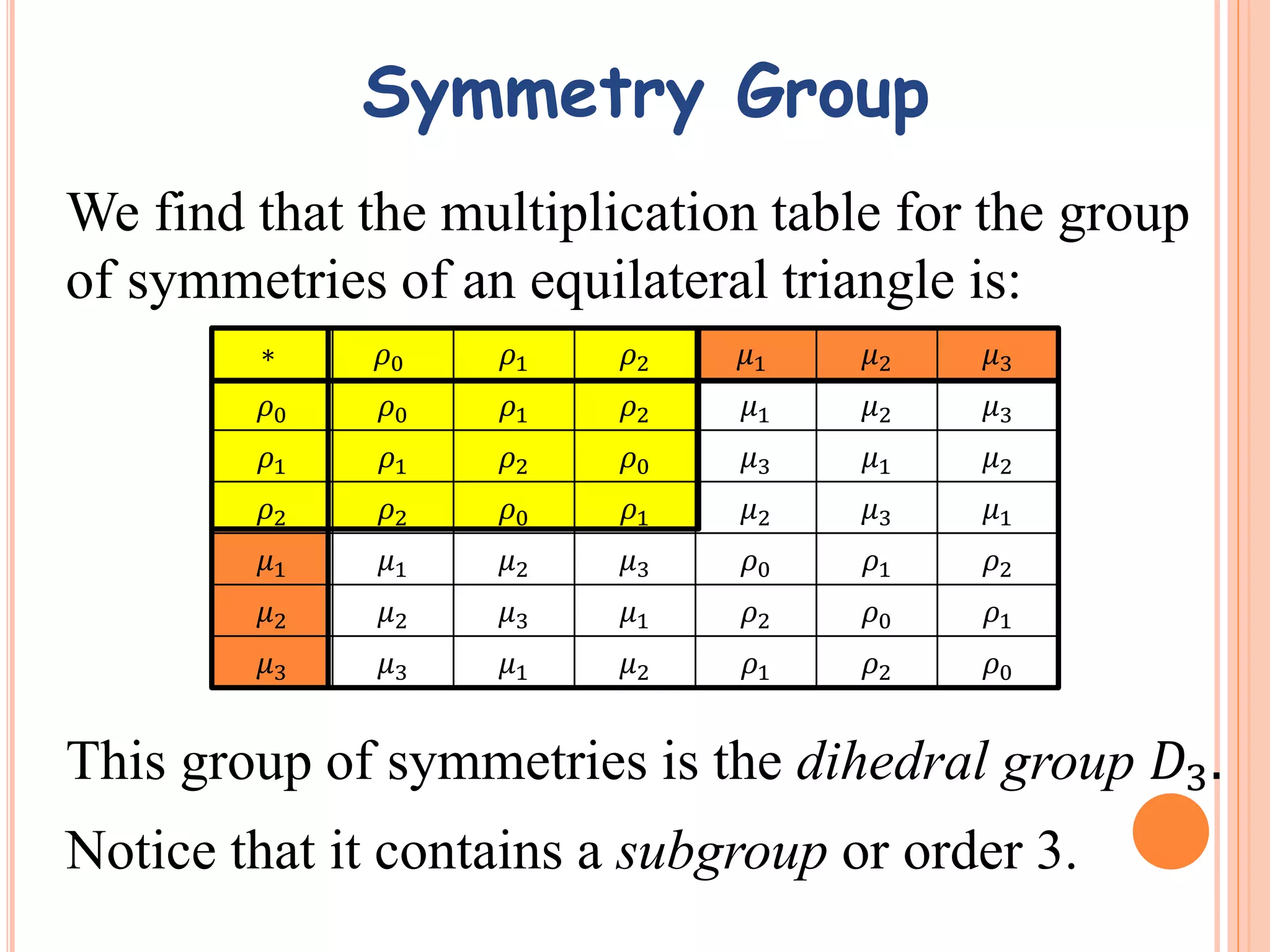
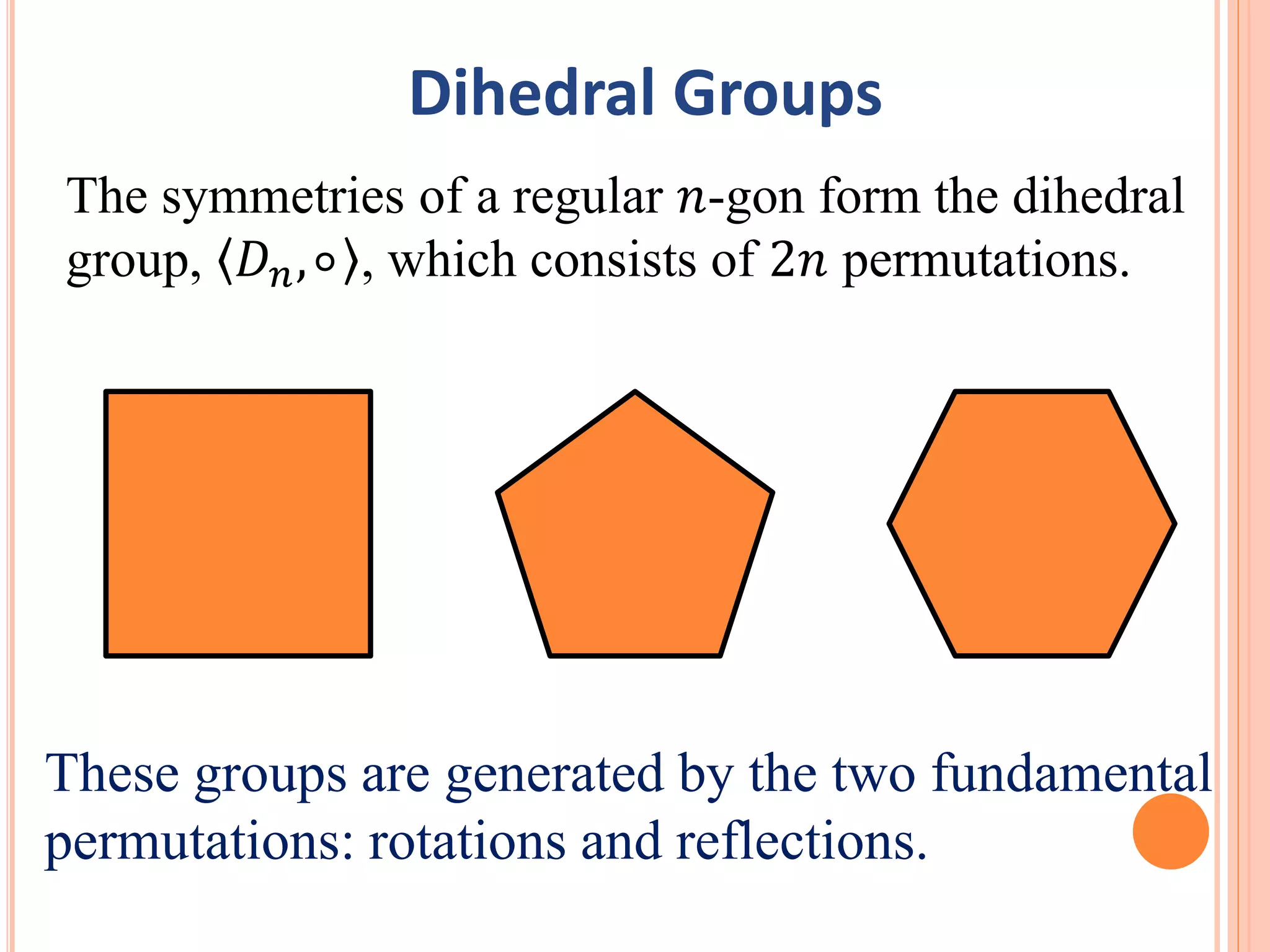
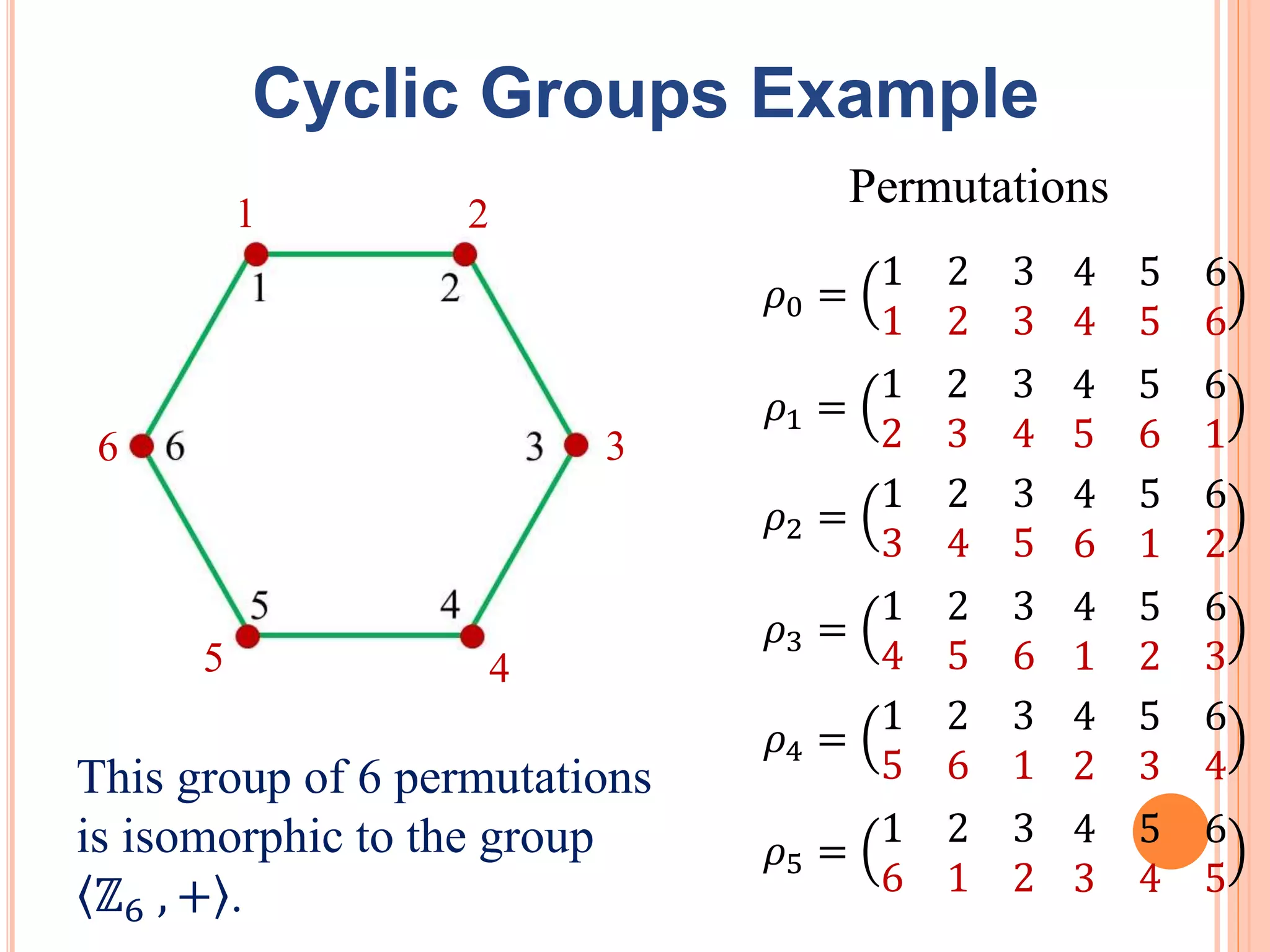
1. The document discusses group theory and provides examples of familiar groups like integers under addition and complex numbers under multiplication. 2. Symmetry groups are introduced, which are sets of isometries that carry a figure onto itself. Examples of symmetry groups of a line segment and equilateral triangle are given. 3. Dihedral groups Dn are defined as the symmetry groups of a regular n-gon and contain rotational and reflective symmetries. Cyclic groups Zn are subgroups of Dn containing only rotational symmetries.

1. ABSTRACT ALGEBRA
GROUP THEORY
Presented by
Ms.S.R.Vidhya,
Assistant Professor of Mathematics,
Bon Secours College for Women, Thanjavur.

2. Groups

3. Familiar Group
• The integers under addition, ℤ, + .
• The real numbers under addition, ℝ , + .
• The complex numbers under addition, ℂ , + .
• The integers modulo n under addition,
ℤ𝑛 , + .
• The rationals under addition, ℚ , + .
In each case, associativity is clear, the identity is 0,
and the inverse of 𝑥 is −𝑥 (in ℤ𝑛, −𝑥 = 𝑛 − 𝑥).
Example : 1

4. • The nonzero rationalsunder
multiplication, ℚ∗
,× .
• The nonzero real numbers under
multiplication, ℝ∗
,× .
• The nonzero complex numbers under
multiplication, ℂ∗
,× .
In each case, associativity is clear, the identity is 1,
and the inverse of 𝑥 is 1/𝑥.
Familiar Group
Example : 2

5. An example of a non-abelian group is the group of
all 𝒏 × 𝒏 invertible matrices under matrix
multiplication:
𝑀𝑛 = 𝐴 =
𝑎1,1 ⋯ 𝑎1,𝑛
⋮ ⋱ ⋮
𝑎𝑛,1 ⋯ 𝑎𝑛,𝑛
𝑎𝑖,𝑗 ∈ 𝑅, det 𝐴 ≠ 0 .
In each of the examples above, the binary operations
(+ or ×) are commutative (that is, 𝑎 + 𝑏 = 𝑏 + 𝑎
and 𝑎 × 𝑏 = 𝑏 × 𝑎). A group in which the binary
operation is commutative is called an abelian group.
Familiar Group
Example : 3

6. It is not the case (in general) that
𝑢 × 𝑣 × 𝑤 = 𝑢 × 𝑣 × 𝑤.
For example, 𝑖 × 𝑖 × 𝑗 = 𝑖 × 𝑘 = −𝑗 but
𝑖 × 𝑖 × 𝑗 = 0 × 𝑗 = 0.
A Strange Example
In the above examples, associativity is “clear.” In fact, it is
rather rare to encounter a binary operation that is not
associative. One such example, which you see in Linear
Algebra and Calculus 3 is the cross product of vectors in ℝ3
.
So we cannot form a group using vectors and the
cross product!

7. Each of the above examples of groups are
“algebraic.” We now introduce groups based on
geometric properties.
Definition. An isometryof n-dimensional space ℝ𝑛
is a function from ℝ𝑛
onto ℝ𝑛
that preserves
distance. [Gallian, page 461]
Geometry and Isometrics
More precisely, 𝜋 is an isometry from ℝ𝑛
to ℝ𝑛
if
for all 𝑥, 𝑦 ∈ ℝ𝑛
we have
𝑑 𝑥, 𝑦 = 𝑑 𝜋 𝑥 , 𝜋 𝑦
where 𝑑 is a metric on ℝ𝑛
.
Symmetry Groups

8. Definition. Let 𝐹 be a set of points in ℝ𝑛
.
The symmetry group of 𝐹 in ℝ𝑛
is the set of
all isometries of ℝ𝑛
that carry 𝐹 onto itself.
The group operation is function composition.
[Gallian, page 461]
Symmetry Groups

9. Symmetry Group
Example. Consider the line segment I in ℝfrom
𝑎 = 0 to 𝑏 = 1. There are two isometries which
map I onto itself: 𝑓0 𝑥 = 𝑥 and 𝑓1 𝑥 = 1 − 𝑥.
1
0 1
0
1
0 1
0
The “multiplication table”
for the symmetry group
with elements 𝑓0 and 𝑓1 is:
𝑓0 𝑓1
𝑓0 𝑓0 𝑓1
𝑓1 𝑓1 𝑓0
°
𝑓0 𝑓1

10. Example. Consider the line segment I in ℝ2from 𝑎 = 0
to 𝑏 = 1. There are four isometries which map I onto
itself:
1. 𝑓0 𝑥, 𝑦 = (𝑥, 𝑦), the identity,
2. 𝑓1 𝑥, 𝑦 = (1 − 𝑥, 𝑦), reflection about the line 𝑥 =
1/2,
3. 𝑓2 𝑥, 𝑦 = (𝑥, −𝑦), reflection about the line 𝑦 = 0,
and
4. 𝑓3 𝑥, 𝑦 = (1 − 𝑥, −𝑦), a combination of 𝑓1 and 𝑓2.
Symmetry Group

11. x
y
x
y
𝑓0
𝑓1
𝑓2
𝑓3
Identity
Reflection about
𝑦 = 0
Reflection about
𝑥 = 1/2
Reflection about
𝑥 = 1/2 and 𝑦 = 0
Symmetry Group
𝑓0 𝑓1 𝑓2 𝑓3
𝑓0 𝑓0 𝑓1 𝑓2 𝑓3
𝑓1 𝑓1 𝑓0 𝑓3 𝑓2
𝑓2 𝑓2 𝑓3 𝑓0 𝑓1
𝑓3 𝑓3 𝑓2 𝑓1 𝑓0
The multiplication
table for this group is
given here. The group
is denoted 𝐷2, .
°
°

12. Symmetry Group Example
1
2
3
Permutations
𝜌0 =
1 2 3
1 2 3
𝜌1 =
1 2 3
2 3 1
𝜌2 =
1 2 3
3 1 2

13. Permutations
𝜇1 =
1 2 3
1 3 2
𝜇2 =
1 2 3
3 2 1
𝜇3 =
1 2 3
2 1 3
1
3 2
Symmetry Group Example

14. Permutations
𝜇1 =
1 2 3
1 3 2
𝜌1 ∗ 𝜇1 =
1 2 3
2 3 1
1 2 3
1 3 2
=
1 2 3
2 1 3
= 𝜇3
1
3 2
Symmetry Group

15. Symmetry Group
Permutations
𝜌1 =
1 2 3
2 3 1
𝜇1 ∗ 𝜌1 =
1 2 3
1 3 2
1 2 3
2 3 1
=
1 2 3
3 2 1
= 𝜇2
1
3 2

16. We find that the multiplication table for the group
of symmetries of an equilateral triangle is:
∗ 𝜌0 𝜌1 𝜌2 𝜇1 𝜇2 𝜇3
𝜌0 𝜌0 𝜌1 𝜌2 𝜇1 𝜇2 𝜇3
𝜌1 𝜌1 𝜌2 𝜌0 𝜇3 𝜇1 𝜇2
𝜌2 𝜌2 𝜌0 𝜌1 𝜇2 𝜇3 𝜇1
𝜇1 𝜇1 𝜇2 𝜇3 𝜌0 𝜌1 𝜌2
𝜇2 𝜇2 𝜇3 𝜇1 𝜌2 𝜌0 𝜌1
𝜇3 𝜇3 𝜇1 𝜇2 𝜌1 𝜌2 𝜌0
This group of symmetries is the dihedral group 𝐷3.
Notice that it contains a subgroup or order 3.
Symmetry Group

17. Dihedral Groups
The symmetries of a regular 𝑛-gon form the dihedral
group, 𝐷𝑛, , which consists of 2𝑛 permutations.
These groups are generated by the two fundamental
permutations: rotations and reflections.
°

18. Cyclic Groups
If we consider the symmetries of a regular 𝑛-gon which
only consist of the rotations (and not the reflections) then
we get a subgroup of the dihedral group𝐷𝑛 which consists
of the 𝑛 rotational permutations.
This group of 𝑛 rotational permutations forms the cyclic
group of order 𝑛. The cyclic group of order 𝑛 is the same as
(i.e., “isomorphic to”) the integers modulo 𝑛, ℤ𝑛 , + .
Since, for each 𝑛, the cyclic group of order 𝑛 is a subgroup
of the dihedral group of order 2𝑛, we often drop the binary
operation and write this as: ℤ𝑛 < 𝐷𝑛.

19. 1 2
3
4
5
6
Permutations
𝜌0 =
1 2 3
1 2 3
4 5 6
4 5 6
𝜌1 =
1 2 3
2 3 4
4 5 6
5 6 1
𝜌2 =
1 2 3
3 4 5
4 5 6
6 1 2
𝜌3 =
1 2 3
4 5 6
4 5 6
1 2 3
𝜌4 =
1 2 3
5 6 1
4 5 6
2 3 4
𝜌5 =
1 2 3
6 1 2
4 5 6
3 4 5
Cyclic Groups Example
This group of 6 permutations
is isomorphic to the group
ℤ6 , + .

20. Generators of a Group
The cyclic group ℤ𝑛 can be “generated” by the elementary
rotation 𝜌1. That is, each element of ℤ𝑛 is a power of 𝜌1:
𝜌2 = 𝜌1 ∗ 𝜌1, 𝜌3 = 𝜌1 ∗ 𝜌1 ∗ 𝜌1, etc. In fact, the formal
definition of a cyclic group is a group which is generated
by a single element.
The dihedral group 𝐷𝑛 can be generated by two
symmetries: a rotation and a reflection. This is the reason
these groups are called dihedral groups.

21. Finite Symmetry Groups
Definition. A group 𝐺,∗ is finite if the set 𝐺 has a finite
number of elements: 𝐺 < ∞.
Theorem. The only finite symmetry groups of a set of
points in ℝ2 (that is, the only “plane symmetry groups” or
“groups of isometries of the plane”) are the groups ℤ𝑛 and
𝐷𝑛 for some 𝑛. These groups are sometimes called rosette
groups. [Fraleigh, page 115; Gallian, page 463]
We now explore infinite plane symmetry groups. This topic
is covered (briefly) in Fraleigh in Section II.12 (“Plane
Isometries”) and in some detail in Gallian’s Chapter 28
(“Frieze Groups and Crystallographic Groups”).