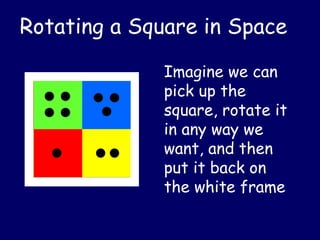
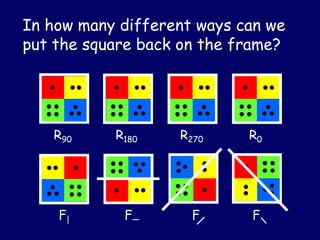
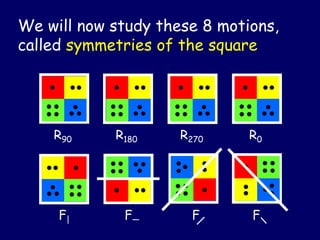
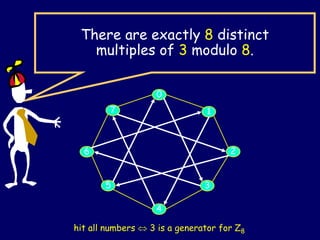
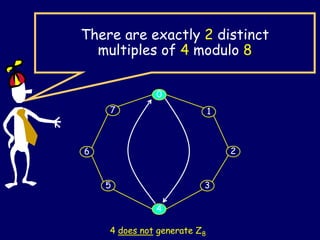
(1) The document discusses algebraic structures like groups, rings, and fields. It provides examples of groups including the symmetries of a square (YSQ) and the integers modulo n (Zn). (2) It then describes the RSA cryptosystem, which is used to securely transmit messages over the internet. It works by having a public and private key based on large prime numbers. (3) The document goes on to define properties of groups like associativity, identities, inverses, generators, orders of elements, and subgroups. It provides examples to illustrate these concepts for groups like YSQ and Zn*.

1. Great Theoretical Ideas In Computer Science
Anupam Gupta CS 15-251 Fall 2006
Lecture 15 Oct 17, 2006 Carnegie Mellon University
Algebraic Structures:
Groups, Rings, and Fields

2. The RSA Cryptosystem
Rivest, Shamir, and Adelman (1978)
RSA is one of the most used
cryptographic protocols on the net. Your
browser uses it to establish a secure
session with a site.

3. Zn = {0, 1, 2, …, n-1}
Zn
* = {x 2 Zn | GCD(x,n) =1}
Quick raising to power.
<Zn, +n>
1. Closed
2. Associative
3. 0 is identity
4. Additive Inverses
Fast + and -
5. Cancellation
6. Commutative
<Zn
*, *n>
1. Closed
2. Associative
3. 1 is identity
4. Multiplicative Inverses
Fast * and /
5. Cancellation
6. Commutative

4. Fundamental lemma of powers.
Suppose x2 Zn
*, and a,b,n are naturals.
If a ´(n) b Then xa ´n xb
Equivalently,
xa ´n xa mod (n)

5. Euler Phi Function
(n) = size of Zn
*
p prime ) Zp
*= {1,2,3,…,p-1}
) (p) = p-1
(pq) = (p-1)(q-1)
if p,q distinct primes

6. The RSA Cryptosystem
Rivest, Shamir, and Adelman (1978)
RSA is one of the most used
cryptographic protocols on the net. Your
browser uses it to establish a secure
session with a site.

7. Pick secret, random large primes: p,q
“Publish”: n = p*q
(n) = (p) (q) = (p-1)*(q-1)
Pick random e  Z*
(n)
“Publish”: e
Compute d = inverse of e in Z*
(n)
Hence, e*d = 1 [ mod (n) ]
“Private Key”: d

8. n,e is my
public key.
Use it to
send me a
message.
p,q random primes, e random  Z*
(n)
n = p*q
e*d = 1 [ mod (n) ]

9. n,
e
p,q prime, e random  Z*
(n)
n = p*q
e*d = 1 [ mod (n) ]
messag
e m
me [mod n]
(me)d ´n m

10. An even simpler system

11. Today we are going to
study the abstract
properties of binary
operations

12. Rotating a Square in Space
Imagine we can
pick up the
square, rotate it
in any way we
want, and then
put it back on
the white frame

13. In how many different ways can we
put the square back on the frame?
R90 R180 R270 R0
F| F— F F

14. R90 R180 R270 R0
F| F— F F
We will now study these 8 motions,
called symmetries of the square

15. Symmetries of the Square
YSQ = { R0, R90, R180, R270, F|, F—, F , F }

16. Composition
Define the operation “” to mean “first do
one symmetry, and then do the next”
For example,
R90  R180
Question: if a,b  YSQ, does a  b  YSQ? Yes!
means “first rotate 90˚
clockwise and then 180˚”
= R270
F|  R90 means “first flip horizontally
and then rotate 90˚”
= F

17. R90 R180 R270
R0 F| F— F F
R0
R90
R180
R270
F|
F—
F
F
R0 R90 R180 R270 F| F— F F
R90
R180
R270
F|
F—
F
F
R180 R270 R0
R270 R0 R90
R0 R90 R180
F F F| F—
F— F| F F
F F F— F|
F F— F
F F| F
F— F F|
F| F F—
R0
R0
R0
R0
R180 R90 R270
R180 R270 R90
R270 R90 R180
R90 R270 R180

18. Some Formalism
If S is a set, S  S is:
the set of all (ordered) pairs of elements of S
S  S = { (a,b) | a  S and b  S }
If S has n elements, how many elements
does S  S have? n2
Formally,  is a function from YSQ  YSQ to YSQ
 : YSQ  YSQ → YSQ
As shorthand, we write (a,b) as “a  b”

19. “” is called a binary operation on YSQ
Definition: A binary operation on a set S is a
function  : S  S → S
Example:
The function f:    →  defined by
is a binary operation on 
f(x,y) = xy + y
Binary Operations

20. Is the operation  on the set of symmetries
of the square associative?
A binary operation  on a set S is
associative if:
for all a,b,cS, (ab)c = a(bc)
Associativity
Examples:
Is f:    →  defined by f(x,y) = xy + y
associative?
(ab + b)c + c = a(bc + c) + (bc + c)? NO!
YES!

21. A binary operation  on a set S is
commutative if
For all a,bS, a  b = b  a
Commutativity
Is the operation  on the set of symmetries
of the square commutative? NO!
R90  F| ≠ F|  R90

22. R0 is like a null motion
Is this true: a  YSQ, a  R0 = R0  a = a?
R0 is called the identity of  on YSQ
In general, for any binary operation  on a set
S, an element e  S such that for all a  S,
e  a = a  e = a
is called an identity of  on S
Identities
YES!

23. Inverses
Definition: The inverse of an element a  YSQ
is an element b such that:
a  b = b  a = R0
Examples:
R90 inverse: R270
R180 inverse: R180
F| inverse: F|

24. Every element in YSQ
has a unique inverse

25. R90 R180 R270
R0 F| F— F F
R0
R90
R180
R270
F|
F—
F
F
R0 R90 R180 R270 F| F— F F
R90
R180
R270
F|
F—
F
F
R180 R270 R0
R270 R0 R90
R0 R90 R180
F F F| F—
F— F| F F
F F F— F|
F F— F
F F| F
F— F F|
F| F F—
R0
R0
R0
R0
R180 R90 R270
R180 R270 R90
R270 R90 R180
R90 R270 R180

26. 3. (Inverses) For every a  S there is
b  S such that:
Groups
A group G is a pair (S,), where S is a set
and  is a binary operation on S such that:
1.  is associative
2. (Identity) There exists an element
e  S such that:
e  a = a  e = a, for all a  S
a  b = b  a = e
If  is commutative, then G is called a
commutative group

27. Examples
Is (,+) a group?
Is + associative on ? YES!
Is there an identity? YES: 0
Does every element have an inverse? NO!
(,+) is NOT a group

28. Examples
Is (Z,+) a group?
Is + associative on Z? YES!
Is there an identity? YES: 0
Does every element have an inverse? YES!
(Z,+) is a group

29. Examples
Is (YSQ, ) a group?
Is  associative on YSQ? YES!
Is there an identity? YES: R0
Does every element have an inverse? YES!
(YSQ, ) is a group

30. Examples
Is (Zn,+) a group?
Is + associative on Zn? YES!
Is there an identity? YES: 0
Does every element have an inverse? YES!
(Zn, +) is a group

31. Examples
Is (Zn
*, *) a group?
Is * associative on Zn
*? YES!
Is there an identity? YES: 1
Does every element have an inverse? YES!
(Zn
*, *) is a group

32. Theorem: A group has at most one identity
element
Proof:
Suppose e and f are both identities of
G=(S,)
Then f = e  f = e
Identity Is Unique

33. Theorem: Every element in a group has a
unique inverse
Proof:
Inverses Are Unique
Suppose b and c are both inverses of a
Then b = b  e = b  (a  c) = (b  a)  c = c

34. A group G=(S,) is finite if S is a finite set
Define |G| = |S| to be the order of the group
(i.e. the number of elements in the group)
What is the group with the least number of
elements?
How many groups of order 2 are there?
G = ({e},) where e  e = e
e
f
e f
e
f
f
e

35. Generators
A set T  S is said to generate the group
G = (S,) if every element of S can be
expressed as a finite product of elements in T
Question: Does {R90} generate YSQ?
Question: Does {S|, R90} generate YSQ?
A single element g  S is called a generator
of G=(S,) if {g} generates G
Does YSQ have a generator?
NO!
YES!
NO!

36. Generators For (Zn,+)
Any a  Zn such that GCD(a,n) = 1 generates Zn
Claim: If GCD(a,n) =1, then the numbers
a, 2a, …, (n-1)a, na are all distinct modulo n
Proof (by contradiction):
Suppose xa = ya (mod n) for x,y  {1,…,n} and x ≠ y
Then n | a(x-y)
Since GCD(a,n) = 1, then n | (x-y), which cannot
happen

37. There are exactly 8 distinct
multiples of 3 modulo 8.
7
5 3
1
0
6 2
4
hit all numbers  3 is a generator for Z8

38. There are exactly 2 distinct
multiples of 4 modulo 8
7
5 3
1
0
6 2
4
4 does not generate Z8

39. There are exactly
LCM(n,c)/c = n/GCD(c,n)
distinct multiples of c modulo n
and hence
elements c with GCD(c,n) = 1
generate Zn

40. If G = (S,), we use an denote (a  a  …  a)
n times
Definition: The order of an element a of G is
the smallest positive integer n such that an = e
Order of an element
Lemma: a is a generator of G if order(a) = |G|

41. If G = (S,), we use an denote (a  a  …  a)
n times
Definition: The order of an element a of G is
the smallest positive integer n such that an = e
The order of an element can be infinite!
Example: The order of 1 in the group (Z,+)
is infinite
What is the order of F| in YSQ? 2
What is the order of R90 in YSQ? 4

42. Orders
What if G is a finite group:
is the order of any element of G finite?
Yes: consider a, a2, a3, a4, a5, …
Since G is finite, at some point aj = ak for some j < k.
Hence ak-j = identity.

43. There are exactly
LCM(n,c)/c = n/GCD(c,n)
distinct multiples of c modulo n
and hence
order(Zn,+)(c) = n/GCD(c,n)

44. What about (Z_n^*, *) ?
What is order of the group Zn
*?
|Zn
*| = φ(n)
Does Zn
* have generators?
What are the orders of elements in Zn
*?

45. Z7
* = {1,2,3,4,5,6}
20 = 1; 21 = 2; 22 = 4; 23 = 1
30=1; 31 = 3; 32 = 2; 33 = 6; 34 =4;
35 = 5; 36 = 1
2 generates {1, 2, 4} Order 3
3 generates {1,2,3,4,5,6} Order 6
3 is a generator, but 2 is not.

46. Theorem (Non-trivial)
Thm: There are φ(n-1) generators of the group (Zn
*, *)
E.g.,
for Z7
*, φ(7-1) = φ(2*3) = 2.
Generators: 3,5
You can check that:
Z7
* = {1, 2, 3, 4, 5, 6}
Orders: 1, 3, 6, 3, 6, 2

47. Theorem:
Let x be an element of G.
The order of x divides the order of G.
Orders
proof coming soon…

48. Subgroups
Given a group G = (S, ), a subset S’  S forms
a subgroup if H = (S’, ) satisfies the group
properties.
That is,
S’ is closed under the group operation 
The identity element of G is also in S'.
The inverse of every element in S’ is also in S’.

49. Examples
Yrot = { R0, R90, R180, R270 }
is a subgroup of
Quick check:
Closure?
Identity?
Inverses?
YSQ = { R0, R90, R180, R270, F|, F—, F , F }

50. Examples
Z8,even = {0, 2, 4, 6}
with the + operation is a subgroup of
Z8 = {0,1,2,3,4,5,6,7}
Quick check:
Closure?
Identity?
Inverses?

51. Lagrange’s Theorem
Theorem: if H is a subgroup of G, then
|H| divides |G|.
Fact: The set generated by any element x  G is a
subgroup of G.
Corollary: the order of any element x  G divides |G|.

52. Proof of Lagrange’s Theorem

53. We can define more than one operation on a set
For example, in Zn we can do addition and
multiplication modulo n
A ring is a set together with two operations
(usually called + and *)
Lord Of The Rings

54. Definition:
A ring R is a set together with two binary
operations + and *, satisfying the following
properties:
1. (R,+) is a commutative group
2. * is associative
3. The distributive laws hold in R:
(a + b) * c = (a * c) + (b * c)
a * (b + c) = (a * b) + (a * c)

55. Examples
Do the integers  form a ring?
(, +) is a commutative group.
* is associative
+ distributes over *…

56. Definition:
A field F is a set together with two binary
operations + and *, satisfying the following
properties:
1. (F,+) is a commutative group
2. (F-{0},*) is a commutative group
3. The distributive law holds in F:
(a + b) * c = (a * c) + (b * c)
Fields

57. Examples
Do the integers  form a field?
(, +) is a commutative group.
but ({0}, *) do not form a group!
there are no multiplicative inverses…

58. Examples
Zp (for prime p) is a field.
(Zp, +) is a commutative group.
(Zp
* = Zp{0}, *) is a commutative group.
The distributive law holds.

59. Examples
The real numbers  form a field.
(, +) is a commutative group.
({0}, *) is a commutative group.
The distributive law holds.

60. CRYPTOGRAPHY based on the
presumed computational difficulty of a
number theoretic problem.
Let p be prime. g be a generator for (Zp
*, *)
DHp.g(x) = gx mod p is fast to compute.
DISCRETE-LOGp,g(r) = x means that gx =r mod p.
No one knows a fast algorithm given a random r to
compute x.

61. Diffie and Hellman [1976]
“New Directions In Cryptography.”
Let p be prime. g be a generator mod p.
Alice: Picks random x 2 Zp-1
Publishes gx mod p
Bob: Picks random y 2 Zp-1
Publishes gy mod p
Both parties can compute (mod p)
(gx)y = (gy)x = gxy mod p-1
Eve sees both
published strings.
Can she figure out
gxy mod p?

62. Diffie Hellman has an *amazing* feature.
Two people who have never met and have no prior
shared secrets can use the system.
Without this property, commerce on the net would
be impossible.
Typical use: Agree on a random string r.
Use r as your secret-key in a more conventional
private-key crypto system

63. Why should I care about any of this?
Groups, Rings and Fields are examples of the
principle of abstraction: the particulars of
the objects are abstracted into a few simple
properties
All the results carry over to any group
In The End…
Ideas central to crypto and other areas!

64. Study Bee
Symmetries of the Square
Compositions
Groups
Binary Operation
Identity and Inverses
Basic Facts: Inverses Are Unique
Generators
Rings and Fields
Definition