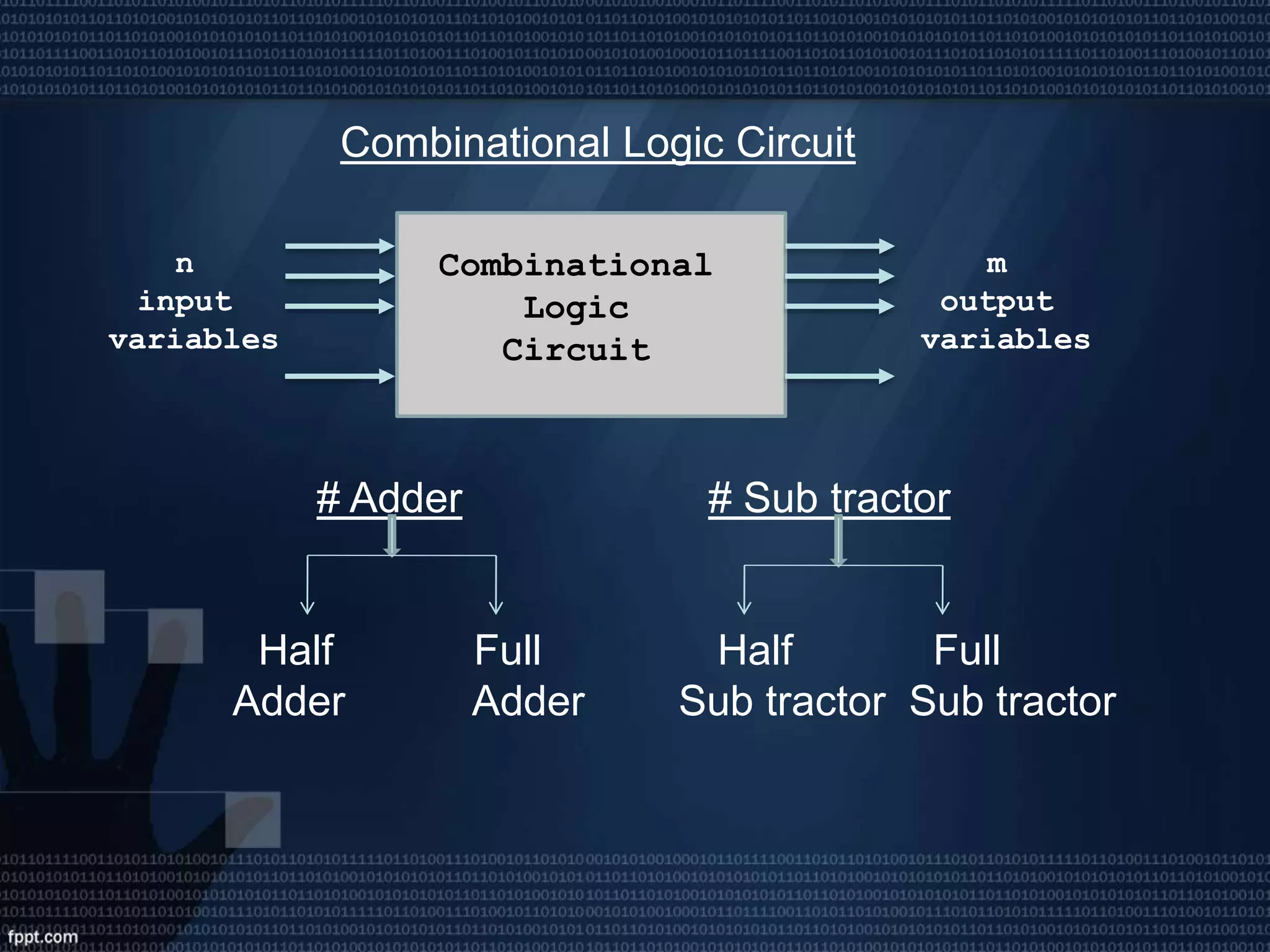
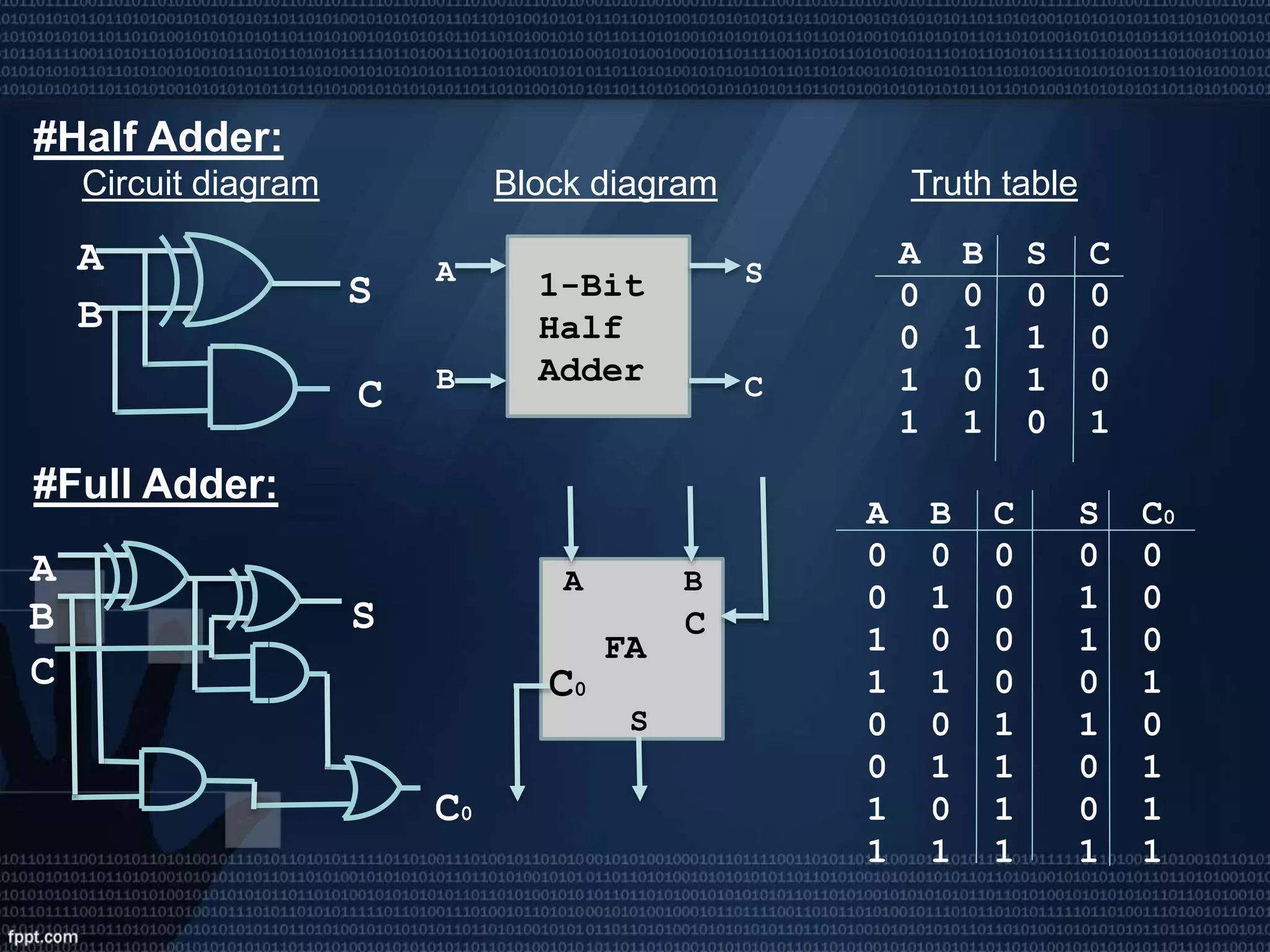
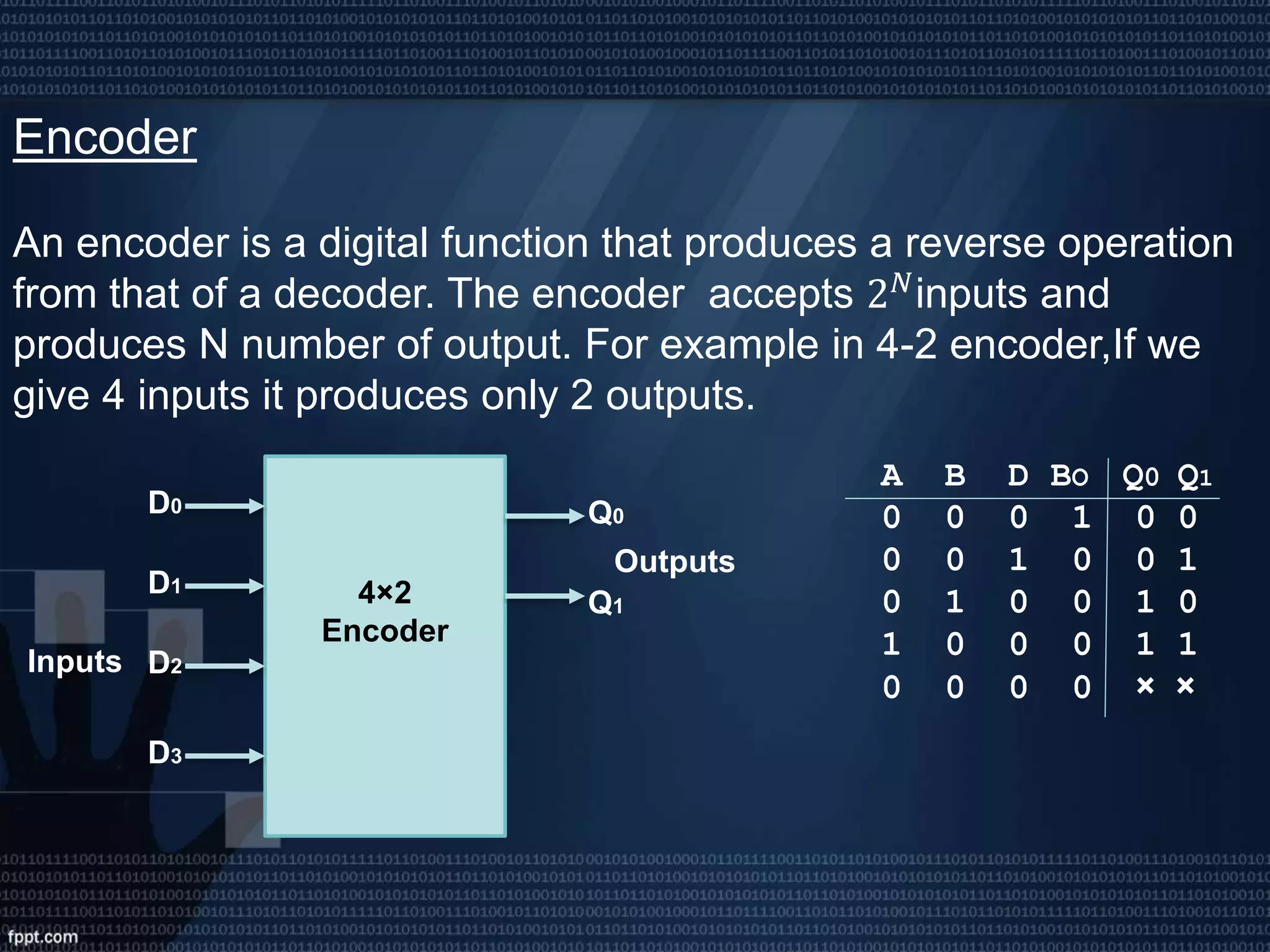
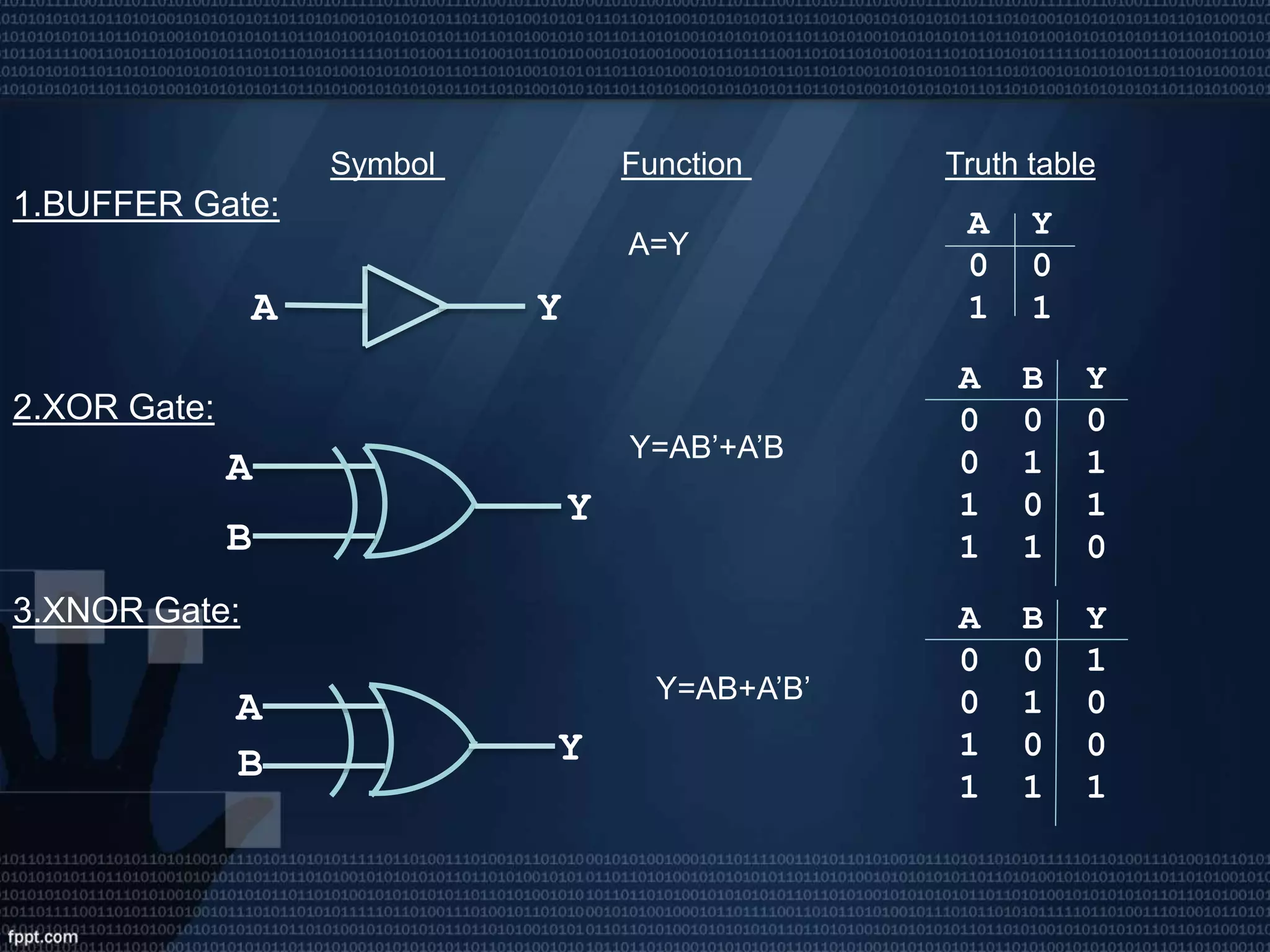
This presentation introduces digital logic circuits such as encoders, decoders, multiplexers, demultiplexers and logic gates. It is presented by a group consisting of 5 members whose names and student IDs are listed. The topics covered include the definitions of complements, combinational logic circuits, encoder and decoder functions, how multiplexers and demultiplexers work, and the truth tables of common logic gates.

1. “Welcome To Our
Presentation”

2. Group Name: A
Group Members
Name ID
• Rafiqul Islam 152-33-2802
• Saurav Roy 152-33-2818
• Mehedi Hasan 152-33-2808
• Raysul Islam Tuhin 152-33-2807
• Tahmina Akter Jui 152-33-2831

3. Presentation Topic:
• Complement
• Combinational Logic Circuit
• Encoder/Decoder
• Multiplexer/De multiplexer
• Logic Gate

4. Complements
# Complements are used in digital computer for simplifying the subtraction
operation and for logical manipulations.
# There are two types of complements
1.The r’s complements
2.The (r-1)’s complements
2’s and 1’s complement for binary number
10’s and 9’s complement for decimal number

5. The r’s complements
A positive number N is base r with an integer part of n digits, the r’s
complement of N is defined as:
𝑟 𝑛
- N
Example:
1.The 10’s complement of (52520) 10 =47180
2. The 2’s complement of (101100) 2 =(10100)2

6. The (r-1)’s complements
A positive number N is base r with an integer part of n digits and a fraction part
of m digits ,the (r-1)’s complement of N is defined as:
𝑟 𝑛
- 𝑟−𝑚
- N
Example:
1.The 9’s complement of (0.3267) 10 =.6732
2. The 1’s complement of (101100) 2 =(010011) 2

7. Combinational Logic Circuit
# Adder # Sub tractor
Half Full Half Full
Adder Adder Sub tractor Sub tractor
n
input
variables
m
output
variables
Combinational
Logic
Circuit

8. A
B
S
C
A B S C
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
A S1-Bit
Half
AdderB C
A
B S
C
C0
#Half Adder:
Circuit diagram Block diagram Truth table
#Full Adder:
A
S
FA
B
C
C0
A B C S C0
0 0 0 0 0
0 1 0 1 0
1 0 0 1 0
1 1 0 0 1
0 0 1 1 0
0 1 1 0 1
1 0 1 0 1
1 1 1 1 1

9. #Half Sub tractor :
Circuit diagram Block diagram Truth table
#Full Sub tractor :
A
B
D
BO
A D
Half
Subtractor
B BO
A B D BO
0 0 0 0
0 1 1 1
1 0 1 0
1 1 0 0
A B Bi D B0
0 0 0 0 0
0 0 1 1 1
0 1 0 1 1
0 1 1 0 1
1 0 0 1 0
1 0 1 0 0
1 1 0 0 0
1 1 1 1 1
A D
Full
SubtractorB
BOBi
A
B D
BO
Bi

10. Encoder
An encoder is a digital function that produces a reverse operation
from that of a decoder. The encoder accepts 2 𝑁inputs and
produces N number of output. For example in 4-2 encoder,If we
give 4 inputs it produces only 2 outputs.
D3
D0
D1
D2
Q0
Q14×2
Encoder
Inputs
Outputs
A B D BO Q0 Q1
0 0 0 1 0 0
0 0 1 0 0 1
0 1 0 0 1 0
1 0 0 0 1 1
0 0 0 0 × ×

11. Decoder
A decoder is a combinational circuit that converts binary
information from n input lines to a maximum of 2 𝑛unique output
line. The decoder accepts N inputs and produces 2 𝑁
number of
output. For example in 3-8 encoder, If we give 3 inputs it produces
8 outputs.
Enable
A
B
C
D0
𝟐 𝟎
D7
D6
D1
D2
D3
D5
D4
0
𝟐 𝟏
𝟐 𝟐
EN
1
2
3
4
5
6
7
Decimal Binary inputs
A B C
Outputs
D0 D1 D2 D3 D4 D5 D6 D7
0 0 0 0 1 0 0 0 0 0 0 0
1 0 0 1 0 1 0 0 0 0 0 0
2 0 1 0 0 0 1 0 0 0 0 0
3 0 1 1 0 0 0 1 0 0 0 0
4 1 0 0 0 0 0 0 1 0 0 0
5 1 0 1 0 0 0 0 0 1 0 0
6 1 1 0 0 0 0 0 0 0 1 0
7 1 1 1 0 0 0 0 0 0 0 1

12. Multiplexer
A digital multiplexer is a combinational circuit that selects binary
information from one to many input liner and directs it to a single
output lines. Normally, there are 2 𝑛input lines and n selection liner.
S0
Enable
S2
8:1
MUX
S1
D0
D7
D1
YD3
D4
Datainputs
Select Inputs
Outputs
Enable
E
Select Inputs
S2 S1 S0
Outputs
Y
0 × × × 0
1 0 0 0 D0
1 0 0 1 D1
1 0 1 0 D2
1 0 1 1 D3
1 0 0 0 D4
1 0 0 1 D5
1 0 1 0 D6
1 0 1 1 D7

13. De multiplexer
A decoder with an enable input is referred to as a decoder.
Normally, there are n input lines and 2 𝑛selection liner. If there are
n data output lines and m select lines then 2 𝑚
=n.
I
S0
D0
D1
D2
D3
1-to-4
DEMUX
S1
Inputs
I
Select
S0 S1
Outputs
D0 D1 D2 D3
1 0 0 1 0 0 0
1 0 1 0 1 0 0
1 1 0 0 0 1 0
1 1 1 0 0 0 1

14. Logic Gate
*A large number of electronic circuits are made up of logic gates. These process signals
which represent true or false.
*There are Three types of basic gate:
Symbol Function Truth table
1.AND Gate:
Y=A.B
2.OR Gate:
Y=A+B
3.NOT Gate:
Y=A’
X Y Z
0 0 0
0 1 0
1 0 0
1 1 1
A
B
Y
X Y Z
0 0 0
0 1 1
1 0 1
1 1 1
X 𝑿′
0 1
1 0
A
B
Y
YA

15. *There are two types of Universal logic gate:
Symbol Function Truth table
1.NAND Gate:
Y= (A.B)’
2.NOR Gate:
Y= (A+B)’
A
B
Y
A
B
Y
A B Y
0 0 1
0 1 1
1 0 1
1 1 0
A B Y
0 0 1
0 1 0
1 0 0
1 1 0

16. Symbol Function Truth table
1.BUFFER Gate:
A=Y
2.XOR Gate:
Y=AB’+A’B
3.XNOR Gate:
Y=AB+A’B’
A Y
0 0
1 1A Y
A
B
Y
A B Y
0 0 0
0 1 1
1 0 1
1 1 0
A
B Y
A B Y
0 0 1
0 1 0
1 0 0
1 1 1