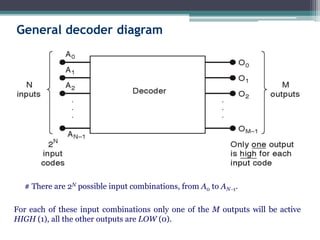
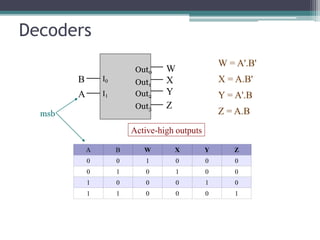
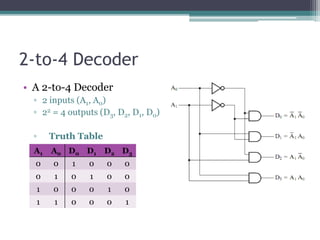
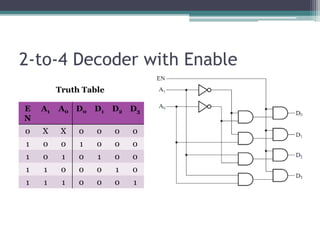
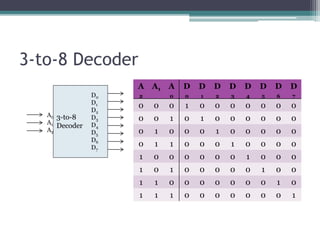
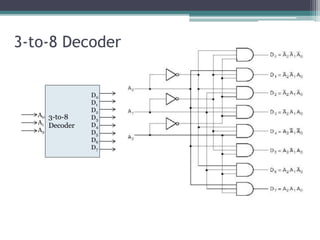
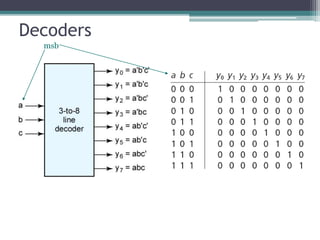
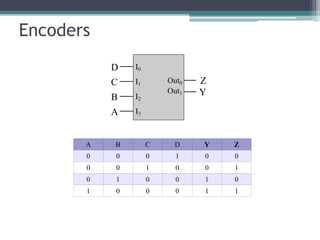
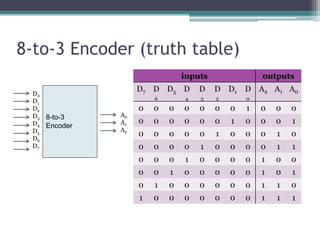
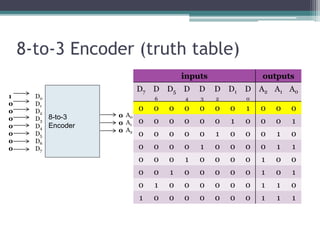
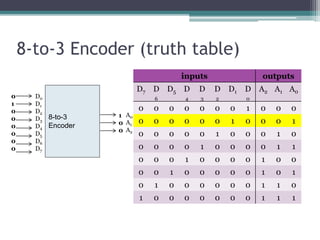
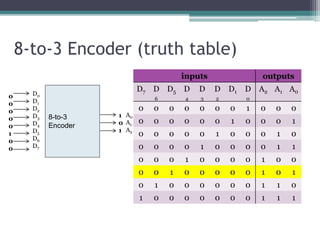
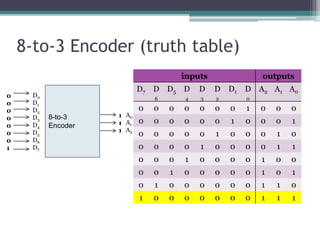
The truth table is not complete because it is missing the encoding for when no inputs are active. A complete truth table would include a row for all zero inputs to specify the output in that case. The output equations are: A0 = D7 A1 = D6 + D5 + D4 + D3 A2 = D2 + D1 + D0 This encodes the highest priority input on the lowest two bits, with the next two highest priorities on the middle bit, and any active input setting the highest bit.

2. Encoder, Decoder, Multiplexor, De-multiplexor

3. Name ID
Muhammad Numan Yousaf 13003065009
Qasim Shehzad 13003065028
Waqar-ul-Malik 13003065050
Seharyar Munir 13003065049
Haseeb-ur-Rehman 13003065034

4. Multiplexer and De-Multiplexer
• A multiplexer is a circuit that accept many input but give
only one output. A de-multiplexer function exactly in the
reverse of a multiplexer, that is a de-multiplexer accepts
only one input and gives many outputs. Generally
multiplexer and de-multiplexer are used together, because
of the communication systems are bi directional.

5. Multiplexer
Multiplexer means many
into one. A multiplexer is a
circuit used to select and
route any one of the several
input signals to a signal
output. An simple example
of an non electronic circuit
of a multiplexer is a single
pole multi position switch.
Single Pole Multi Position
Switch

6. Uses of Multiplexers
Multi-position switches are
widely used in many
electronics circuits. However
circuits that operate at high
speed require the multiplexer
to be automatically selected. A
mechanical switch cannot
perform this task satisfactorily.
Therefore, multiplexer used to
perform high speed switching
are constructed of electronic
components. Multiplexer

7. Types of Multiplexer
• Multiplexer handle two type of data that is analog
and digital. For analog application, multiplexer
are built of relays and transistor switches. For
digital application, they are built from standard
logic gates.
• The multiplexer used for digital applications, also
called digital multiplexer, is a circuit with many
input but only one output. By applying control
signals, we can steer any input to the output. Few
types of multiplexer are 2-to-1, 4-to-1, 8-to-1, 16-
to-1 multiplexer.

8. 4-to-1 Multiplexer
The 4-to-1 multiplexer has 4
input bit, 2 control bits, and 1
output bit. The four input
bits are I0,I1,I2 and I3. only
one of this is transmitted to
the output y. The output
depends on the value of S0
and S1 which is the control
input. The control input
determines which of the
input data bit is transmitted
to the output.
4-to-1 multiplexer

9. 4-to-1 Multiplexer
S1 S0 F
0 0 I0
0 1 I1
1 0 I2
1 1 I3

10. 4-to-1 Multiplexer
• An example of 4-to-1 multiplexer is IC 74153 in
which the output is same as the input.
• Another example of 4-to-1 multiplexer is 45352
in which the output is the compliment of the
input.
• Example of 16-to-1 line multiplexer is IC74150.

11. Applications of Multiplexer
• Multiplexer are used in various fields where
multiple data need to be transmitted using a
single line. Following are some of the
applications of multiplexers
• Communication system
• Telephone network
• Computer memory
• Transmission from the computer system of a
satellite

12. De-multiplexer
De-multiplexer means one to
many. A de-multiplexer is a
circuit with one input and
many output. By applying
control signal, we can steer
any input to the output. Few
types of de-multiplexer are 1-
to 2, 1-to-4, 1-to-8 and 1-to
16 de-multiplexer 1-to-4
De- multiplexer

13. 1-to-4 De-Multiplexer
A B Y0 Y1 Y2 Y3
0 0 I 0 0 0
0 1 0 I 0 0
1 0 0 0 I 0
1 1 0 0 0 I

14. Applications of De-Multiplexer
• De-multiplexer is used to connect a single
source to multiple destinations. The main
application area of de-multiplexer is
communication system where multiplexer are
used.
• Communication System
• ALU (Arithmetic Logic Unit)
• Serial to parallel converter

15. Decoders
 A decoder has
 N inputs
 2N
outputs
 A decoder selects one of 2N
outputs by
decoding the binary value on the N inputs.
 The decoder generates all of the min-terms of
the N input variables.
 Exactly one output will be active for each
combination of the inputs.

16. Decoders
•A decoder is a logic circuit that accepts a set of inputs that
represents a binary number and activates only the output that
corresponds to the input number.
•In other words, a decoder circuit looks at its inputs,
determines which binary number is present there, and activates
the one output that corresponds to that number ; all other
outputs remain inactive

17. General decoder diagram
# There are 2N possible input combinations, from A0 to AN1.
For each of these input combinations only one of the M outputs will be active
HIGH (1), all the other outputs are LOW (0).

18. Decoders
A B W X Y Z
0 0 1 0 0 0
0 1 0 1 0 0
1 0 0 0 1 0
1 1 0 0 0 1
Active-high outputs
B
W
X
Y
Z
I0
I1A
Out0
Out1
Out2
Out3
W = A'.B'
X = A.B'
Y = A'.B
Z = A.Bmsb

19. 2-to-4 Decoder
• A 2-to-4 Decoder
▫ 2 inputs (A1, A0)
▫ 22 = 4 outputs (D3, D2, D1, D0)
▫ Truth Table
A1 A0 D0 D1 D2 D3
0 0 1 0 0 0
0 1 0 1 0 0
1 0 0 0 1 0
1 1 0 0 0 1

20. 2-to-4 Decoder with Enable
E
N
A1 A0 D0 D1 D2 D3
0 X X 0 0 0 0
1 0 0 1 0 0 0
1 0 1 0 1 0 0
1 1 0 0 0 1 0
1 1 1 0 0 0 1
Truth Table

21. 3-to-8 Decoder
A
2
A1 A
0
D
0
D
1
D
2
D
3
D
4
D
5
D
6
D
7
0 0 0 1 0 0 0 0 0 0 0
0 0 1 0 1 0 0 0 0 0 0
0 1 0 0 0 1 0 0 0 0 0
0 1 1 0 0 0 1 0 0 0 0
1 0 0 0 0 0 0 1 0 0 0
1 0 1 0 0 0 0 0 1 0 0
1 1 0 0 0 0 0 0 0 1 0
1 1 1 0 0 0 0 0 0 0 1
3-to-8
Decoder
D0
D1
D2
D3
D4
D5
D6
D7
A0
A1
A2

22. 3-to-8 Decoder
3-to-8
Decoder
D0
D1
D2
D3
D4
D5
D6
D7
A0
A1
A2

23. Decoders
msb

24. Encoders
 An encoder has
 2N
inputs
 N outputs
 An encoder outputs the binary value of the selected
(or active) input.
 An encoder performs the inverse operation of a
decoder.
 Issues
 What if more than one input is active?
 What if no inputs are active?

25. Encoders
A B C D Y Z
0 0 0 1 0 0
0 0 1 0 0 1
0 1 0 0 1 0
1 0 0 0 1 1
D
Z
Y
I0
I1C
B I2
I3A
Out0
Out1

26. Priority Encoders
 If more than one input is active, the higher-order
input has priority over the lower-order input.
 The higher value is encoded on the output
 A valid indicator, d, is included to indicate whether
or not the output is valid.
 Output is invalid when no inputs are active
 d = 0
 Output is valid when at least one input is active
 d = 1

27. 8-to-3 Encoder (truth table)
8-to-3
Encoder
D0
D1
D2
D3
D4
D5
D6
D7
A0
A1
A2
inputs outputs
D7 D
6
D5 D
4
D
3
D
2
D1 D
0
A2 A1 A0
0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0 0 1
0 0 0 0 0 1 0 0 0 1 0
0 0 0 0 1 0 0 0 0 1 1
0 0 0 1 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0 1 0 1
0 1 0 0 0 0 0 0 1 1 0
1 0 0 0 0 0 0 0 1 1 1

28. 8-to-3 Encoder (truth table)
8-to-3
Encoder
D0
D1
D2
D3
D4
D5
D6
D7
A0
A1
A2
1
0
0
0
0
0
0
0
0
0
0
inputs outputs
D7 D
6
D5 D
4
D
3
D
2
D1 D
0
A2 A1 A0
0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0 0 1
0 0 0 0 0 1 0 0 0 1 0
0 0 0 0 1 0 0 0 0 1 1
0 0 0 1 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0 1 0 1
0 1 0 0 0 0 0 0 1 1 0
1 0 0 0 0 0 0 0 1 1 1

29. 8-to-3 Encoder (truth table)
8-to-3
Encoder
D0
D1
D2
D3
D4
D5
D6
D7
A0
A1
A2
0
1
0
0
0
0
0
0
1
0
0
inputs outputs
D7 D
6
D5 D
4
D
3
D
2
D1 D
0
A2 A1 A0
0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0 0 1
0 0 0 0 0 1 0 0 0 1 0
0 0 0 0 1 0 0 0 0 1 1
0 0 0 1 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0 1 0 1
0 1 0 0 0 0 0 0 1 1 0
1 0 0 0 0 0 0 0 1 1 1

30. 8-to-3 Encoder (truth table)
8-to-3
Encoder
D0
D1
D2
D3
D4
D5
D6
D7
A0
A1
A2
0
0
0
0
0
1
0
0
1
0
1
inputs outputs
D7 D
6
D5 D
4
D
3
D
2
D1 D
0
A2 A1 A0
0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0 0 1
0 0 0 0 0 1 0 0 0 1 0
0 0 0 0 1 0 0 0 0 1 1
0 0 0 1 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0 1 0 1
0 1 0 0 0 0 0 0 1 1 0
1 0 0 0 0 0 0 0 1 1 1

31. 8-to-3 Encoder (truth table)
8-to-3
Encoder
D0
D1
D2
D3
D4
D5
D6
D7
A0
A1
A2
0
0
0
0
0
0
0
1
1
1
1
inputs outputs
D7 D
6
D5 D
4
D
3
D
2
D1 D
0
A2 A1 A0
0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0 0 1
0 0 0 0 0 1 0 0 0 1 0
0 0 0 0 1 0 0 0 0 1 1
0 0 0 1 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0 1 0 1
0 1 0 0 0 0 0 0 1 1 0
1 0 0 0 0 0 0 0 1 1 1

32. 8-to-3 Encoder (equations)
8-to-3
Encoder
D0
D1
D2
D3
D4
D5
D6
D7
A0
A1
A2
inputs outputs
D7 D
6
D5 D
4
D
3
D
2
D1 D
0
A2 A1 A0
0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0 0 1
0 0 0 0 0 1 0 0 0 1 0
0 0 0 0 1 0 0 0 0 1 1
0 0 0 1 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0 1 0 1
0 1 0 0 0 0 0 0 1 1 0
1 0 0 0 0 0 0 0 1 1 1
Note: This truth table is not complete! Why?
Output equations:
A0 = ?
A1 = ?
A2 = ?

33. 8-to-3 Encoder (equations)
8-to-3
Encoder
D0
D1
D2
D3
D4
D5
D6
D7
A0
A1
A2
inputs outputs
D7 D
6
D5 D
4
D
3
D
2
D1 D
0
A2 A1 A0
0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0 0 1
0 0 0 0 0 1 0 0 0 1 0
0 0 0 0 1 0 0 0 0 1 1
0 0 0 1 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0 1 0 1
0 1 0 0 0 0 0 0 1 1 0
1 0 0 0 0 0 0 0 1 1 1
Output equations:
A0 = D1 + D3 + D5 + D7
A1 = ?
A2 = ?

34. 8-to-3 Encoder (equations)
8-to-3
Encoder
D0
D1
D2
D3
D4
D5
D6
D7
A0
A1
A2
inputs outputs
D7 D
6
D5 D
4
D
3
D
2
D1 D
0
A2 A1 A0
0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0 0 1
0 0 0 0 0 1 0 0 0 1 0
0 0 0 0 1 0 0 0 0 1 1
0 0 0 1 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0 1 0 1
0 1 0 0 0 0 0 0 1 1 0
1 0 0 0 0 0 0 0 1 1 1
Output equations:
A0 = D1 + D3 + D5 + D7
A1 = D2 + D3 + D6 + D7
A2 = ?

35. 8-to-3 Encoder (equations)
8-to-3
Encoder
D0
D1
D2
D3
D4
D5
D6
D7
A0
A1
A2
inputs outputs
D7 D
6
D5 D
4
D
3
D
2
D1 D
0
A2 A1 A0
0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0 0 1
0 0 0 0 0 1 0 0 0 1 0
0 0 0 0 1 0 0 0 0 1 1
0 0 0 1 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0 1 0 1
0 1 0 0 0 0 0 0 1 1 0
1 0 0 0 0 0 0 0 1 1 1
Output equations:
A0 = D1 + D3 + D5 + D7
A1 = D2 + D3 + D6 + D7
A2 = D4 + D5 + D6 + D7