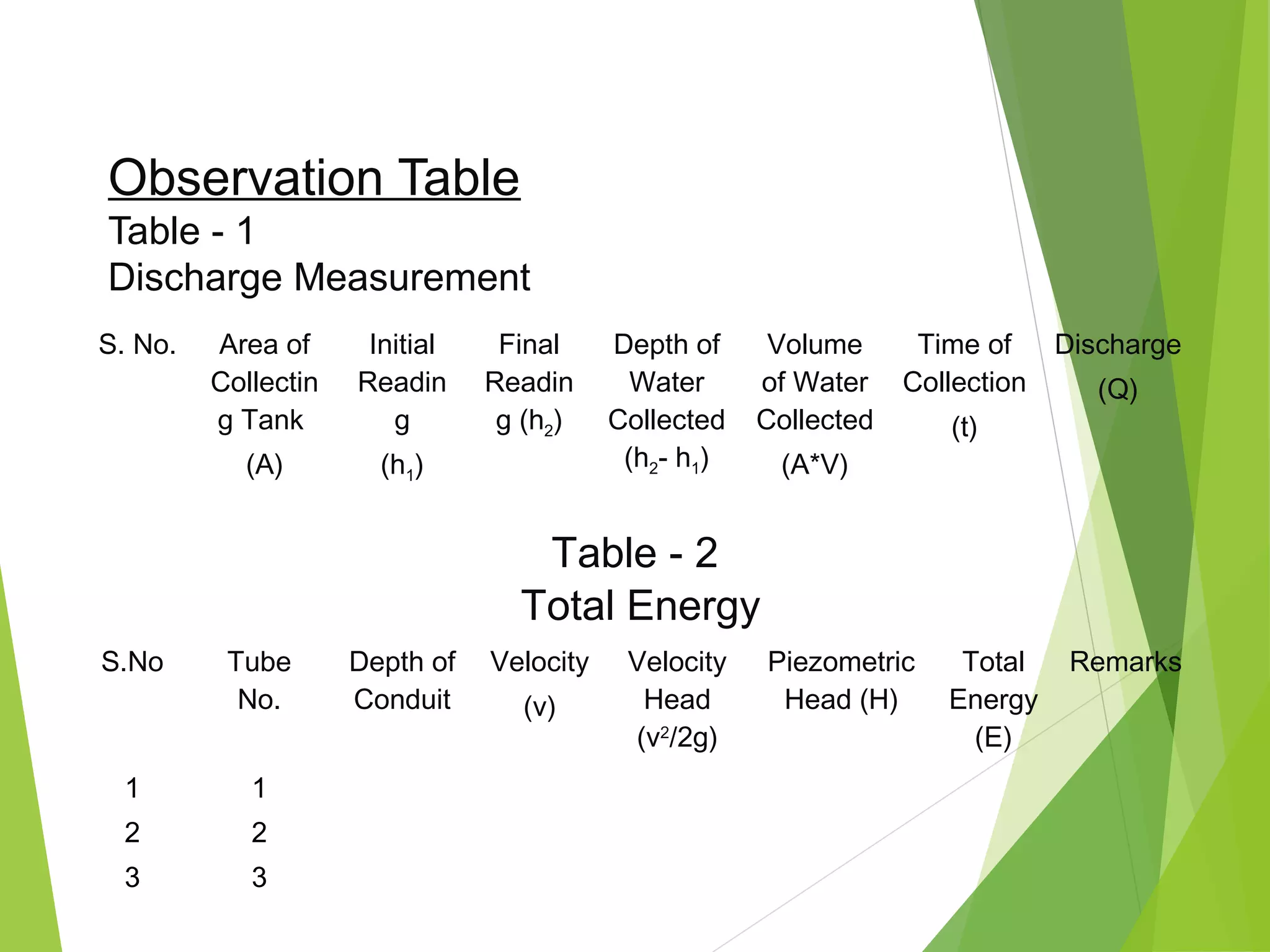
This document describes an experiment to verify Bernoulli's theorem. Bernoulli's theorem states that for an inviscid, incompressible fluid flowing steadily through a closed passage, the total energy at any point remains constant. The experiment involves measuring the pressure, velocity, and elevation at different points in a diverging duct carrying water. Observations are recorded and used to plot the total energy line, which should be horizontal according to Bernoulli's theorem. The results support the theorem by showing the total energy remains constant despite changes in pressure, velocity, and elevation along the duct.

1. Verification of Bernoulli’s Theorem
Bernoulli’s equation states that in a steady, irrotational flow of an ideal
incompressible fluid, the total energy at any point/ section is constant.

2. Object

To verify the Bernoulli's Theorem experimentally.

3. Theory
The principle of conversation of energy gives rise to Bernoulli's
theorem which states that in a pipe flow
if an incompressible ideal fluid flows through a closed passage,
the total head, i.e. the sum of datum head ‘z’, pressure head
(p/w) and velocity head (v2/2g) will be the constant at all
points, i.e.
H= (p/w) +z + (v2/2g)
The validity of above theorem is subject to the following
conditions
(i) the flow being steady,
(ii) fluid being frictionless, i.e. non-viscous
(iii) flow being irrotational, and,
(iv) no external work on the flow system is done by any
external machine

4. Experimental setup
The apparatus consist of diverging duct (e.g. 38mm
width) issuing out of a water container and discharging
into another. peizometric connections are made at
small equal intervals to show pressure heads at
different sections. The discharge is measured by
collecting a known volume of water in time t.

5. The water is supplied to apparatus from the laboratory storage tank
which can be regulated by inlet valve. Another valve is fitted at the
end of duct to get sufficiently low pressure at the central tube. A
graph is attached to vertical board to take the piezometric readings.
Alternatively, a scale may be used for same purpose.

8. Procedure
1. Open the inlet valve to obtain a steady flow. Collect
the water in tank for certain time ‘t’.
(col. 2,3)
2. Consider the base of the apparatus as base datum;
measure the height of water level in the tube above
base, (p/w) +z
(col. 9)
Note: (p/w) is the pressure head and ‘z’ is the datum
head and the sum of these two quantities is called
piezometric head. By proper adjustment of outlet
valve, sufficiently deep curve can be obtained.
3. Note down the width ‘b’, and depth ‘d’ of the duct at
various cross sectional
(col. 5)

9. Formula used
• Q = A1v1=A2v2
• E = z+(p/w)+(v2 /2g) ….
• E1= E2 = E3 =… = constant
where,
(continuity equation)
( total energy of flow)
(Bernoulli equation)
z = datum head
(p/w) = pressure head
(v2/2g) = velocity head

10. Observation Table
Table - 1
Discharge Measurement
S. No.
Area of
Collectin
g Tank
Initial
Readin
g
(A)
Final
Readin
g (h2)
(h1)
Depth of
Water
Collected
(h2- h1)
Volume
of Water
Collected
(A*V)
Time of
Discharge
Collection
(Q)
(t)
Table - 2
Total Energy
S.No
Tube
No.
1
1
2
2
3
3
Depth of
Conduit
Velocity
(v)
Velocity
Head
(v2/2g)
Piezometric
Head (H)
Total
Energy
(E)
Remarks

11. Presentation of Results
1.
Mark on the graph the ordinate of (p/w+z)
on a suitably chosen horizontal scale which
is called Hydraulic Gradient Line (H.G.L.).
2.
Mark velocity head (v2/2g) over (p/w+z)
curve. It is called Total Energy Line
(T.E.L.).
3.
Show that the resulting curve is a mildly
sloping straight-line adding to it the loss of
head, result in a horizontal line. Thus, it
proves the Bernoulli's theorem.

12. Precautions
1.
Discharge should be kept constant throughout one
set of observation.
2.
Depth of passage should be very carefully observed.

13. Viva-voce
1.
2.
3.
4.
5.
6.
7.
8.
What is meant by incompressible and ideal fluid?
What difference does it make to the Bernoulli's theorem if the
flowing medium is not ideal fluid but real one?
Is the theorem applicable to gases and vapors too?
Discuss this point ?
Are the datum, pressure and velocity energies interconvertible ?
Give example of each ?
What is meant by irrotational flow?
If a prime mover or any other machine is installed between
any two flow sections, how is it accounted for in Bernoulli's
theorem?