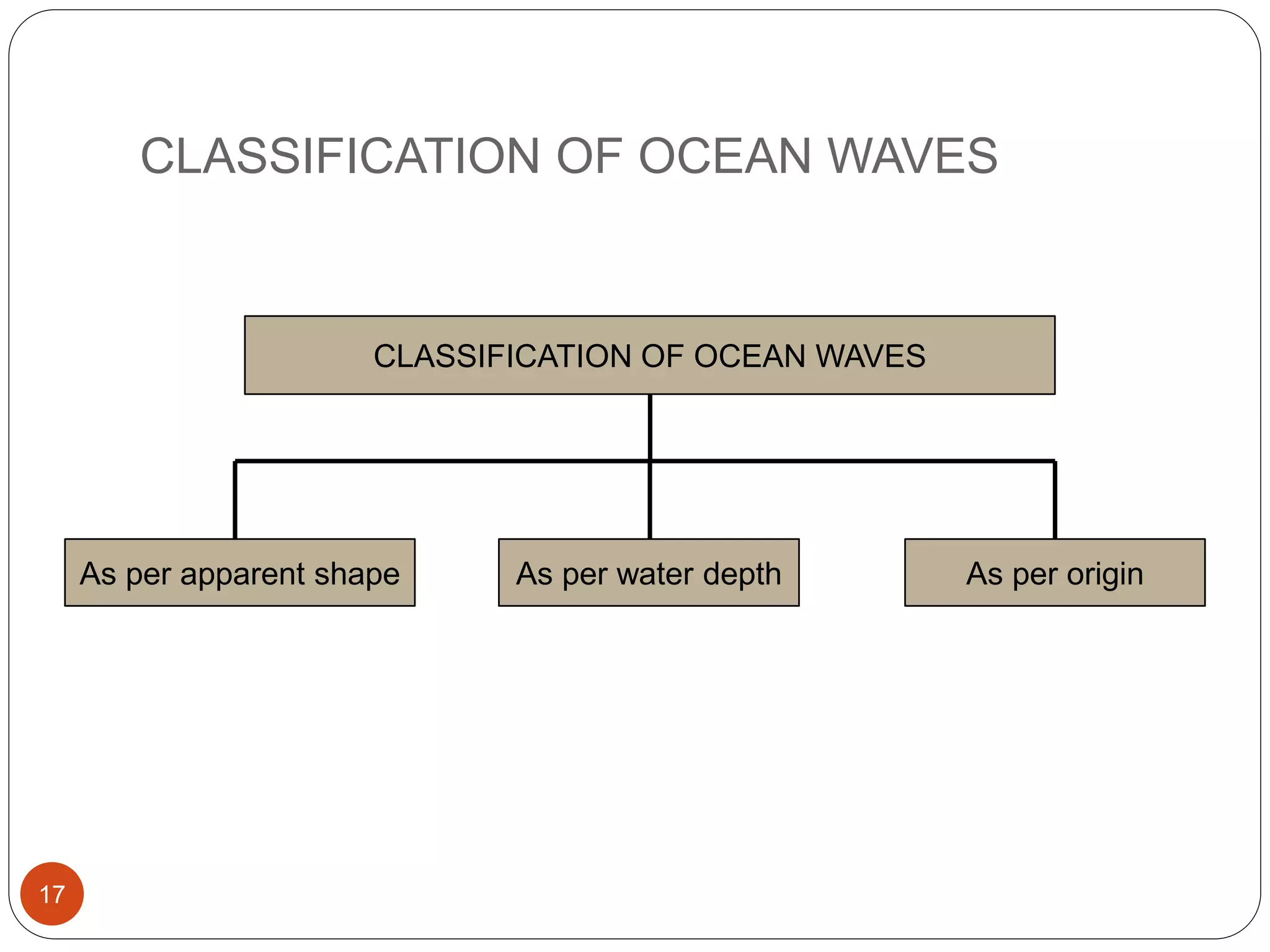
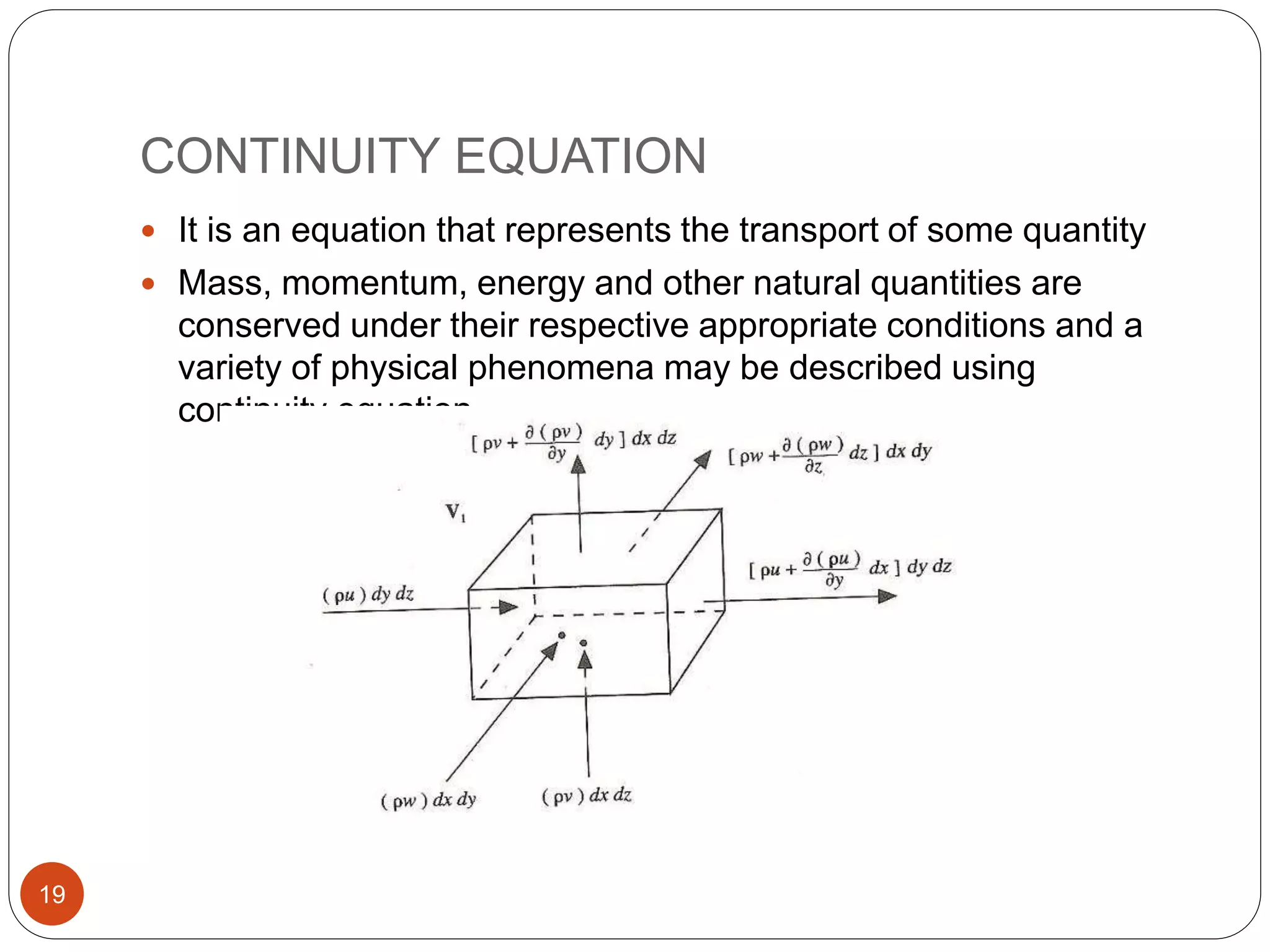
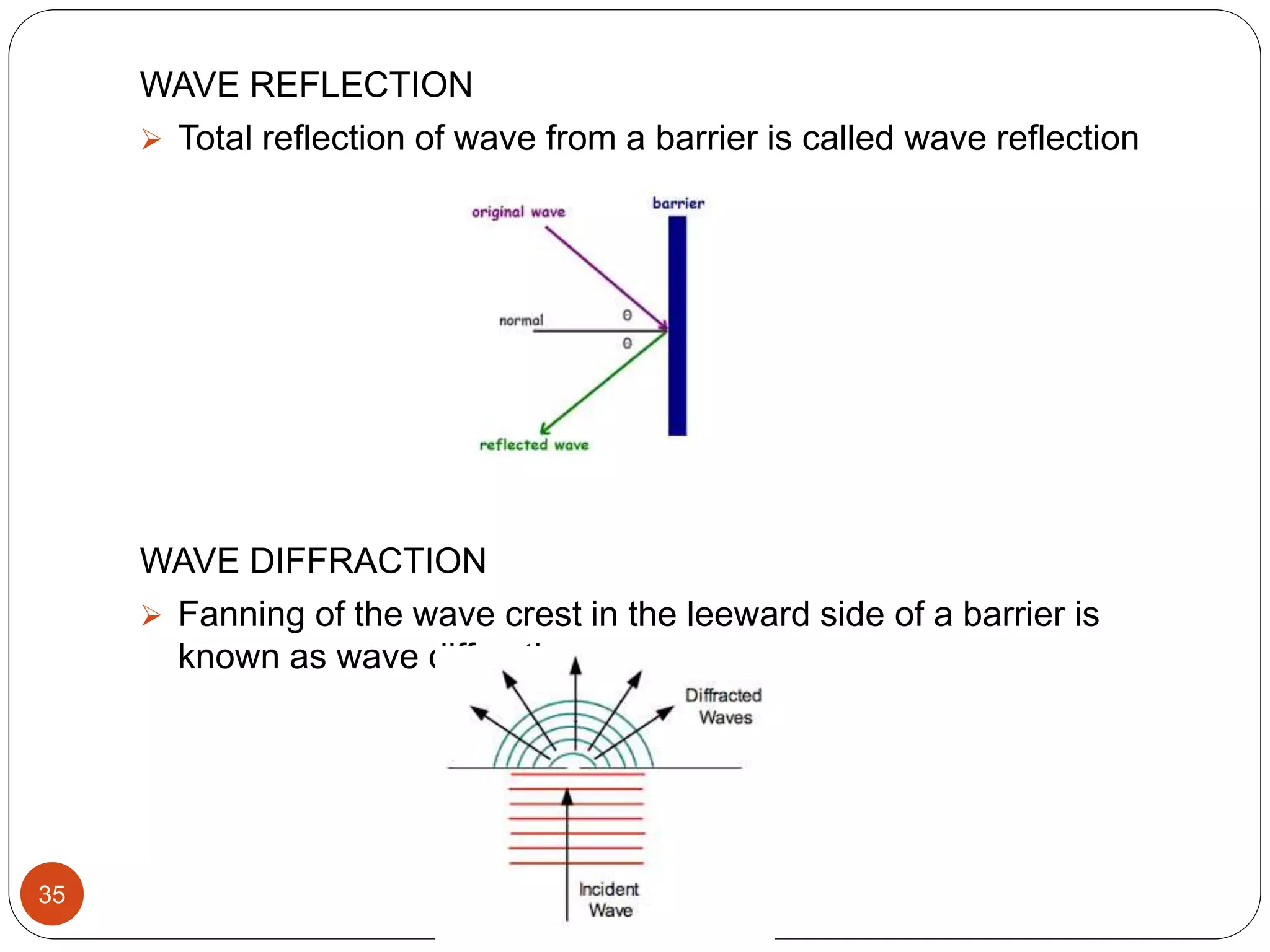
This document provides an overview of fluid mechanics and wave hydrodynamics. It defines key terms like fluids, waves, currents and tides. It describes the fundamental equations of fluid mechanics including continuity, Euler, Navier-Stokes and Bernoulli's equations. It also covers topics like classification of flows, wave generation, propagation and transformation processes like refraction, reflection and diffraction. The document is intended as an introduction to fluid mechanics and wave concepts for students of coastal and harbour engineering.

1. Mridula G M
Mtech Coastal &Harbour Engineering
KUFOS
WAVE HYDRODYNAMICS
1

2. FLUID MECHANICS
2

3. INTRODUCTION
 The behaviour of waves in the ocean governs the driving forces
responsible for the different kinds of phenomena in the marine
environment
 Three states of matter that exists in nature -- solid, liquid and gas
 Liquid and gas are referred to as fluids.
 Main distinction between liquid and gas lies in their rate of change of
density
 If the change of the density of a fluid is negligible, it is then defined
as incompressible.
3

4. TYPES OF FLUID
1. Ideal fluid : a fluid with no viscosity, no surface tension and is
incompressible.
2. Real fluid : A fluid that has viscosity, surface tension and is
compressible.
3. Compressible fluid : will reduce its volume in the presence of
external pressure.
4. Incompressible fluid : is a fluid that does not change the volume of
the fluid due to external pressure.
4

5. HISTORY OF FM
 Real fluid does not yield good estimates on the forces on
structures due to fluid flow
 It was realised by Navier (1822)
 Thus the viscous flow theory was introduced including a viscous
term to the momentum conservation equation.
 Similarly after few years Stokes (1845) also developed viscous
flow theory
 This momentum conservation equation describing viscous flow is
termed as Navier -Stokes Equation
5

6. TYPES OF FLOW
1. Steady and unsteady flow ( change of fluid characteristics with
respect to time)
2. Uniform and non uniform flow (change of fluid characteristics
with respect to space)
3. Laminar and turbulent flow (movement of particles in layers
and zig-zag
motion)
4. Rotational and irrotational flow (rotation of fluid particles about
their mass centers)
6

7. 7

8. FORCES ACTING ON FLUIDS IN MOTION
1. Gravity force, Fg
2. Pressure force, Fp
3. Viscous force, Fv
4. Turbulent force, Ft
5. Surface tension force, Fs
6. Compressibility force or elastic force, Fe
 By Newton’s law of motion for fluids, ie , rate of change of
momentum is equal to force causing the motion, we have the
equation of motion as:
Ma = Fg + Fp + Fv + Ft + Fs + Fe
Where M is the mass and a is the acceleration of the fluid8

9.  In most of the fluid problems Fe and Fs may be neglected, hence
Ma = Fg + Fp + Fv + Ft
 Then above equation is known as Reynold’s Equation of Motion
 For laminar flows, Ft is negligible, hence
Ma = Fg + Fp + Fv
 Then the above equation is known as Navier Stokes Equation
 In case of ideal fluids, Fv is zero, hence
Ma = Fg + Fp
 Then the above equation is known as the Euler’s Equation of
Motion
9

10. INTRODUCTION TO HYDRODYNAMICS
 Oceans cover 71% of Earth’s surface and contain 97% of Earth’s
water
 Largest ocean is the Pacific ocean and covers about 30% of
Earth’s surface
 In order to explore and exploit the resources, a knowledge on the
ocean environment is essential
 To have a knowledge on the physics of waves ,tides and
currents, the subject of wave hydrodynamics is important.
10

11. TIDES
 The rise and fall of water surface due to the combined effect of
the gravitational forces exerted by the Sun ,Moon and the
rotation of the Earth
 From Newton’s law of universal gravitation
 Therefore, greater the mass of objects and the closer they are to
each other, the greater the gravitational attraction between them.
 Because of this, Sun’s tide generating force is about half that of
the Moon
1 2
2
m m
F
d

11

12.  TIDAL RANGE: the vertical distance between high tide and low tide.
Range is upto 15m.
 CLASSIFICATION
1. Diurnal: have one HT and one LT daily
2. Semidiurnal: have two HT and two LT daily
3. Mixed: there will two HT and two LT daily
but of unequal shape
12

13. CURRENTS
 The flow of mass of water due to the existence of a gradient, ie,
variation of any of the following
• Temperature
• Pressure
• Salinity
• Waves
• Density
 Have magnitude and direction
 We need the information on current because:
o Current exerts forces on structures
o Presence of current in an environment dominated by waves, the characteristics of
wave will be altered
13

14. ACCORDING TO THE FORCES BY WHICH THEY
ARE CREATED
Wind force Tides Waves Density differences
Permanent
Periodical
Accidental
Rotating
Reversing
Hydraulic
Shoreward
Longshore
Seaward
Surface
Sub surface
Deep
CLASSIFICATION OF CURRENTS
14

15. WAVES
 Wave is an oscillation accompanied by the transfer of energy
 Wind gives energy for the growth of ocean waves
 The motion of the surface of waves are considered to be oscillatory
 Water droplet move in a vertical circle as the wave passes. The
droplet moves forward with the wave's crest and backward with the
trough
Waves oscillatory
motion
15

16. GENERATION OF OCEAN WAVES
 Winds pumps in energy for the growth of the ocean waves
 Wind energy is partly transformed into wave energy by
surface(normal and tangential) shear.
 As wind continuously blows over the surface, more energy is
transferred and wave energy increases, ie, wave height increases
 Thus generation is depended on 3 factors:
• Fetch (area where wind blows)
• Velocity
• duration
16

17. CLASSIFICATION OF OCEAN WAVES
CLASSIFICATION OF OCEAN WAVES
As per water depth As per originAs per apparent shape
17

18. FUNDAMENTALS OF FLUID FLOW
1. Conservation of mass ( Continuity Equation)
2. Euler’s Equation
3. Navier Stokes equation (Conservation of Momentum)
4. Bernoulis Equation ( Conservation of Energy)
18

19. CONTINUITY EQUATION
 It is an equation that represents the transport of some quantity
 Mass, momentum, energy and other natural quantities are
conserved under their respective appropriate conditions and a
variety of physical phenomena may be described using
continuity equation
19

20.  Simplify and we get:
𝜕𝜌
𝜕𝑡
+
𝜕(𝜌𝑢)
𝜕𝑥
+
𝜕(𝜌𝑣)
𝜕𝑦
= 0
For three dimensions,
𝜕𝜌
𝜕𝑡
+
𝜕(𝜌𝑢)
𝜕𝑥
+
𝜕(𝜌𝑣)
𝜕𝑦
+
𝜕(𝜌𝑤)
𝜕𝑧
= 0
 The continuity equation is applicable for steady , unsteady flows and
uniform, non-uniform flows and compressible and incompressible
fluids.
 For steady flows,
𝜕ρ
𝜕𝑡
= 0
𝜕(𝜌𝑢)
𝜕𝑥
+
𝜕(𝜌𝑣)
𝜕𝑦
+
𝜕(𝜌𝑤)
𝜕𝑧
= 0
Above equation becomes,
20

21.  For incompressible fluids,
𝜕𝑢
𝜕𝑥
+
𝜕𝑣
𝜕𝑦
+
𝜕𝑤
𝜕𝑧
= 0
 This equation is the continuity equation, ie, “net mass of fluid flowing
across boundaries into an element over a short period must be equal
to the amount by which the mass of element increases during the
same period”.
The mass density of the fluid does not change with x, y, z and t,
hence the above equation simplifies to,
21

22. EULER’S EQUATION OF MOTION
 Only pressure forces and the fluid weight or in general, the body
force are assumed to be acting on the mass of the fluid motion.
Ma = Fg + Fp
 Mass of fluid in the medium is considered as (ρ.Δx. Δy. Δz)
 Component of body force in x direction =X(ρ.Δx. Δy. Δz)
 Net pressure force Fpx acting on the fluid mass :
 Pressure force per unit volume
px
p
F . x. y. z
x

    

px
p
F
x

 

22

23.  For Euler’s equation of motion in X direction
 On solving in X, Y and Z direction we get,
X direction =
Y direction =
Z direction =
 These equations are called Euler’s equation of motion.
 ax, ay, az are termed as total accelerations in respective directions
Max = Fgx + Fpx
x
1 p
X a
x

 

y
1 p
Y a
y

 

z
1 p
Z a
z

 

23

24.  Total acceleration has two components with respect to space and
time
 Euler equations are applicable to compressible and incompressible,
non-viscous in steady or unsteady state of flow.
x
u u u u
a u v w
t x y z
   
   
   
y
v v v v
a u v w
t x y z
   
   
   
z
w w w w
a u v w
t x y z
   
   
   
local acceleration
or
temporal acceleration convective acceleration
24

25. NAVIER -STOKES EQUATION
 It is a generalisation of Euler’s equation of motion (inviscid)
Ma = Fg + Fp + Fv
 It is the most important equation in fluid mechanics
 Rate of change of momentum in an element = sum of net momentum
flux in the element and
external forces
 When shear forces are included along with Euler’s equation, an extra
force term is introduced
𝐷𝑢
𝐷𝑡
=
𝜕𝑢
𝜕𝑡
+ 𝑢
𝜕𝑢
𝜕𝑥
+ 𝑣
𝜕𝑢
𝜕𝑦
+ 𝑤
𝜕𝑢
𝜕𝑧
= −
1
𝜌
𝜕𝑃
𝜕𝑥
+ 𝛻2 𝑢 + 𝑓𝑥
25

26. 26
𝜇
𝜕2 𝑣
𝜕𝑥2
+ 𝜇
𝜕2 𝑣
𝜕𝑦2
+ 𝜇
𝜕2 𝑣
𝜕𝑧2
− 𝛻𝑝 = 𝜌
𝜕𝑣
𝜕𝑡
+ 𝜌𝑣. 𝛻𝑣
 In vector notation ,this can be written as
𝜇 𝛻. 𝛻 𝑣 − 𝛻𝑝 = 𝜌
𝜕𝑣
𝜕𝑡
+ 𝜌𝑣. 𝛻𝑣
 This is the navier stokes equation
𝜕𝑣
𝜕𝑡
+ 𝑣. 𝛻𝑣 = −
1
𝜌
𝛻𝑝 +
𝜇
𝜌
𝛻2 𝑣

27. BERNOULI’S EQUATION
 Bernouli’s equation is related with pressure, velocity and elevation
changes of a fluid in motion.
 “In an ideal fluid, when the flow is steady and continuous, the sum of
pressure energy, kinetic energy and potential energy is a constant”.
Where,
v- fluid flow speed
g- acceleration due to gravity
z- elevation of the point above a reference plane
p- pressure
ρ- density of the fluid
27

28.  Bernouli’s equation is called as the law of conservation of energy.
 APPLICATIONS
It is mainly applied in incompressible fluid problems and also in areas involving
energy. The application of Bernouli’s equation is used in measuring devices such as
 Venturimeter
 Pitot tube
 Orificemeter
28

29. CLASSIFICATION OF FLOW PROBLEMS
Based on flow characteristics and degree of complexity:
1. Laminar and turbulent
2. Time dependent (steady/ transient)
3. Nature of flow field (parabolic/ elliptic)
4. Dimensionality of flow field ( 1D, 2D, 3D)
5. Newtonian and non newtonian
6. Single phase or multiphase flow
29

30. INTRODUCTION TO WAVES
30

31. PARAMETERS TO DEFINE A WAVE
 The main parameters are:
1. Wave height: vertical distance between crest and trough
2. Wave period: time taken to travel one wavelength
3. Wavelength: distance between two successive crest or trough
31

32. WAVE THEORY
LINEAR WAVE THEORY
 Developed by Airy in 1845 gave a mathematical description for the
progressive waves applicable for a wide range of depth to
wavelength ratio.
 It is assumed that water surface elevation is very small when
compared with wave length and water depth and thus it is also
known as ‘small amplitude wave theory’.
 The condition is to obtain the solution to Laplace equation
 The boundary conditions specified are:
o Bottom boundary condition : vertical velocity at bed is zero
o Kinematic free surface boundary condition: surface elevation= vertical water
particle velocity
o Dynamic free surface boundary condition: specifies pressure distribution over free
2 2
2 2
0
x z
  
 
 
32

33. SOLUTION TO LAPLACE EQUATION
 Velocity potential function is given by
∅ =
𝑎𝑔𝑐𝑜𝑠ℎ 𝑘(ℎ + 𝑧)
𝜎 cosh 𝑘ℎ
{Sin kx − σ𝑡 }
 Wave surface elevation
η = a cos(𝑘𝑥 − 𝜎𝑡)
 Wave celerity
 Dispersion relation
𝜎2 = 𝑔𝑘 tanh(𝑘ℎ)
x 2 L L
C
t k T 2 T
 

   
33

34. WAVE TRANSFORMATION
 As wave enters from deep to coastal waters wavelength, celerity
and approach angle reduces.
 Wave height decreases or increases depending upon the
configuration of the coast
 Wave transformation processes are refraction, diffraction and
reflection
WAVE REFRACTION
 A change in alignment of the wave crest line as wave advances
from deep to shallow waters is called wave refraction.
34

35. WAVE REFLECTION
 Total reflection of wave from a barrier is called wave reflection
WAVE DIFFRACTION
 Fanning of the wave crest in the leeward side of a barrier is
known as wave diffraction.
35

36. WAVE BREAKING
 A phenomena in which the surface of the waves folds or rolls
over and intersects itself.
 They are of four types
1. Plunging breaker : wave crest advances faster than celerity
2. Spilling breaker : crest separates and starts rolling down to the
front face of the wave
3. Surging breaker : along steeper coast, the wave rolls up and
down along the steeper face
4. Collapsing breaker : breaking other than above fall under this
category.
plunging breaker spilling breaker
36

37. DELFT 3D
37

38. DELFT3D - WAVE
 Computes the evolution of random short crested waves in
coastal regions with deep, intermediate and shallow waters and
surrounding currents.
 Waves are described with action balance equations
 All information about sea surface is contained in wave energy
density spectrum E(σ,Ɵ) distributing wave energy over
frequencies(σ) and propagation direction (Ɵ).
 The spectrum used is action density spectrum, since, in the
presence of currents, action density is conserved, ie. N(σ,Ɵ).
 It is assumed that current is uniform with respect to vertical
coordinate
 The variables are relative frequency σ and wave direction Ɵ
𝐴𝑐𝑡𝑖𝑜𝑛 𝑑𝑒𝑛𝑠𝑖𝑡𝑦 =
𝐸𝑛𝑒𝑟𝑔𝑦 𝑑𝑒𝑛𝑠𝑖𝑡𝑦
𝑅𝑒𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦38

39.  It is given by
𝜕𝑁
𝜕𝑡
+
𝜕𝑐 𝑥 𝑁
𝜕𝑥
+
𝜕𝑐 𝑦 𝑁
𝜕𝑦
+
𝜕𝑐 𝜎 𝑁
𝜕𝜎
+
𝜕𝑐 𝜃 𝑁
𝜕𝜃
=
𝑆
𝜎
where 𝑐 𝑥, 𝑐 𝑦 are propagation velocity in X and Y direction

𝜕𝑁
𝜕𝑡
- local rate of change of action density with time

𝜕𝑐 𝑥 𝑁
𝜕𝑥
,
𝜕𝑐 𝑦 𝑁
𝜕𝑦
- propagation of action in geographical space

𝜕𝑐 𝜎 𝑁
𝜕𝜎
- shifting of relative frequency with respect to depth and
currents

𝜕𝑐 𝜃 𝑁
𝜕𝜃
- depth induced and current induced refraction
 S – represents generation, dissipation and non linear wave-
wave interactions
wind by whitecapping
bottom friction
depth induced breaking
39

40. DELFT3D - FLOW
 Models 2D and 3D unsteady flow and transports resulted from
tidal or meteorological forces.
 Used to predict flow in shallow seas, coastal waters, estuaries,
lagoons, rivers and lakes.
 For interaction between waves and currents , coupled with
DELFT3D- WAVE.
 If fluid is vertically homogeneous 2D approach is made. Eg storm
surge, tsunami, seiches
 3D modelling is used where flow field is not vertically
homogeneous. Eg dispersion of cooling water in lakes, salt
intrusion in estuary, thermal stratification40

41. PHYSICAL PROCESS
 Solves unsteady shallow water equation in 2D and 3D obtained
by solving Navier-Stokes 3D equation for incompressible flows
 The system of equations include continuity equation, horizontal
equation of motion and transport equation
 Includes mathematical formulations to account for certain
phenomena
 Free surface gradients
 Coriolis force
 Turbulence
 Transport of salt and heat
 Tidal force at open boundaries
 Radiation stresses
 Flow through hydraulic structures ..etc
41

42. FLOW MODEL
 Uses Navier-Stokes equation since it is used to model water
flows
Ma = Fg + Fp + Fv
 It is given by
 This equation is valid if density is constant or Boussinesq
approximation is applied.
ASSUMPTION 1: BOUSSINESQ APPROXIMATION
 “If density variations are small then it may be assumed to be a
constant in all terms except gravitational term”42

43.  Reynold’s averages NS equation is obtained by
ASSUMPTION 2: SHALLOW WATER
1. Horizontal length scale is much larger than the vertical length
scale
2. Vertical velocity is small in comparison with horizontal velocity
 Thus the momentum equation in vertical direction reduces to
hydrostatic pressure distribution
 Integrating and neglecting the atmospheric and horizontal
pressure gradients we obtain
43

44.  And along with this the incompressible continuity equation
are called shallow water equations.
44

45. CONCLUSION
45
 Delft3d Wave solves action balance equation and Flow solves
Navier Stokes equation for incompressible fluids.
 From wave model we obtain significant wave height, mean
wavelength, wave steepness etc.
 From Flow model we obtain depth averaged velocity, bed shear
stress, horizontal viscosity etc.
 These models are run for determining fluid velocity and pressure
in a given geometry.

46. THANK YOU