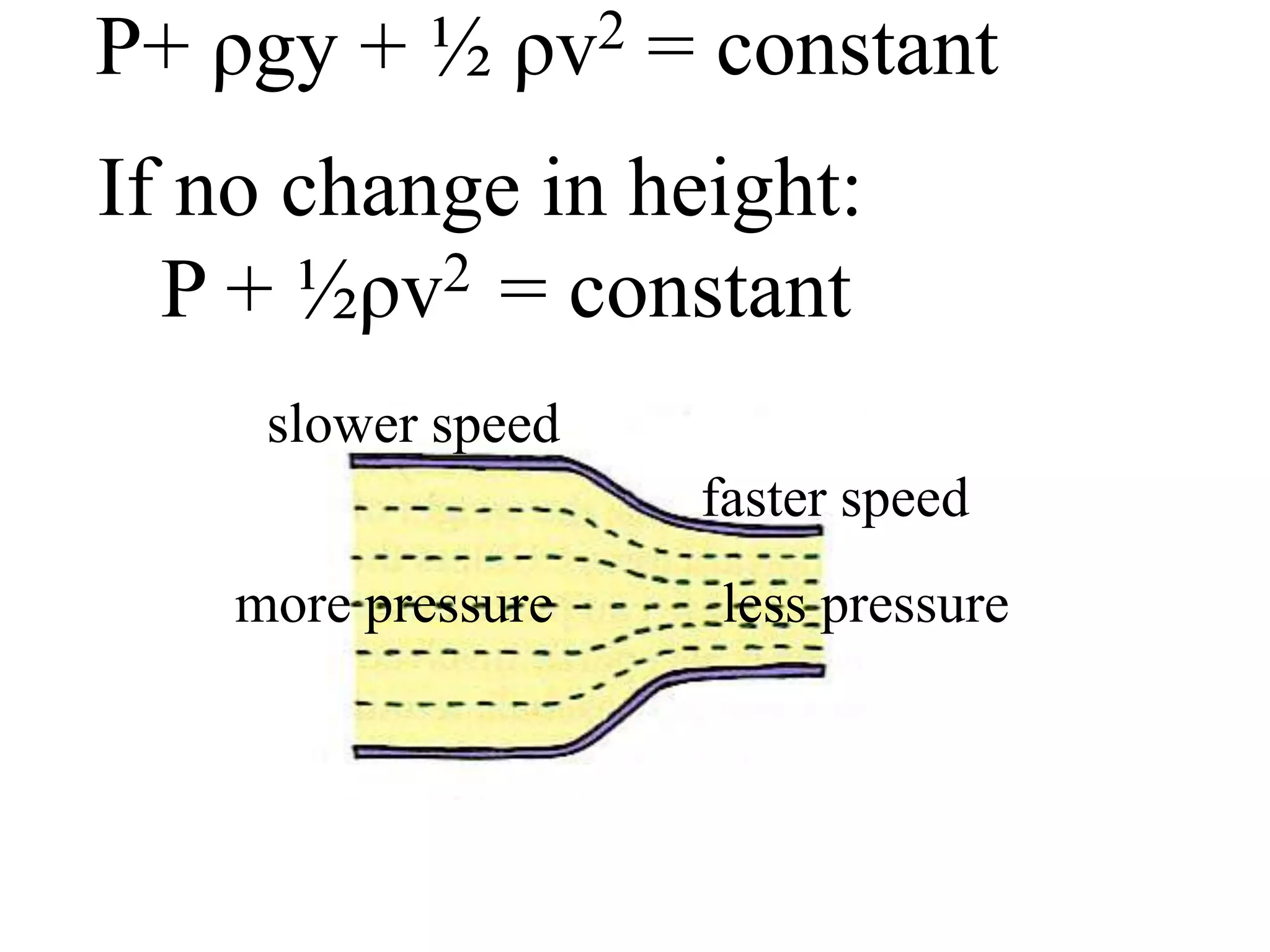
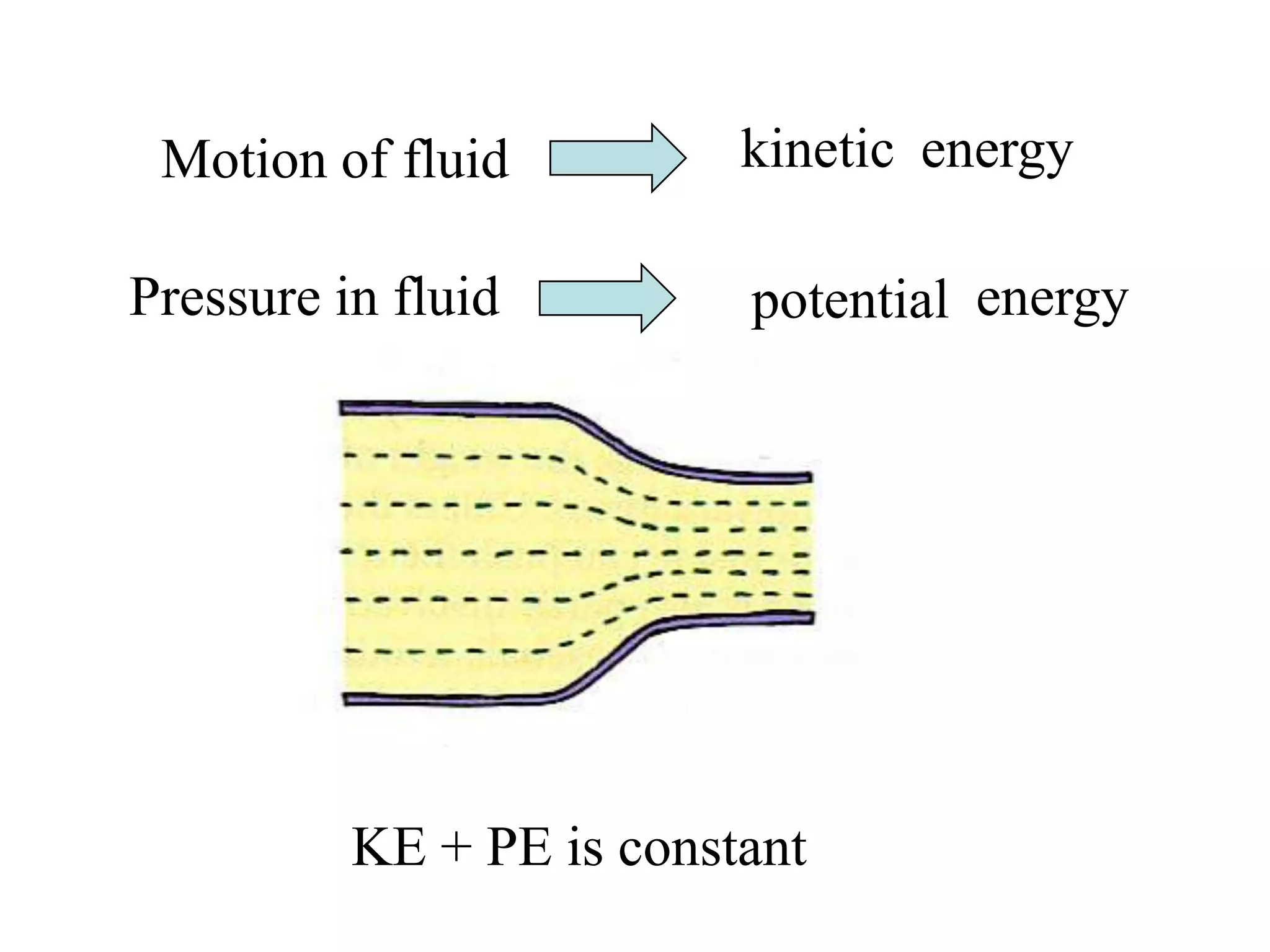
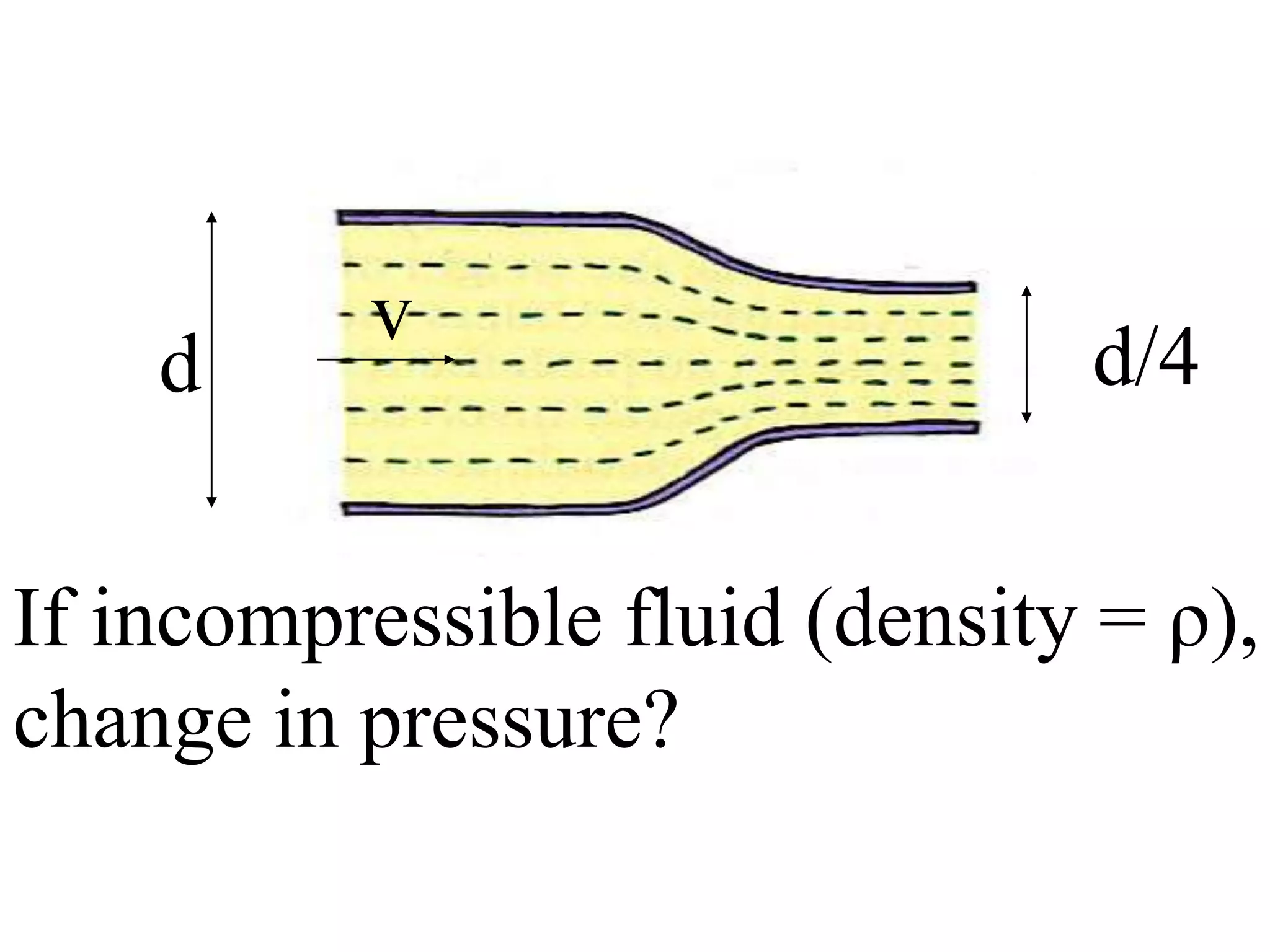
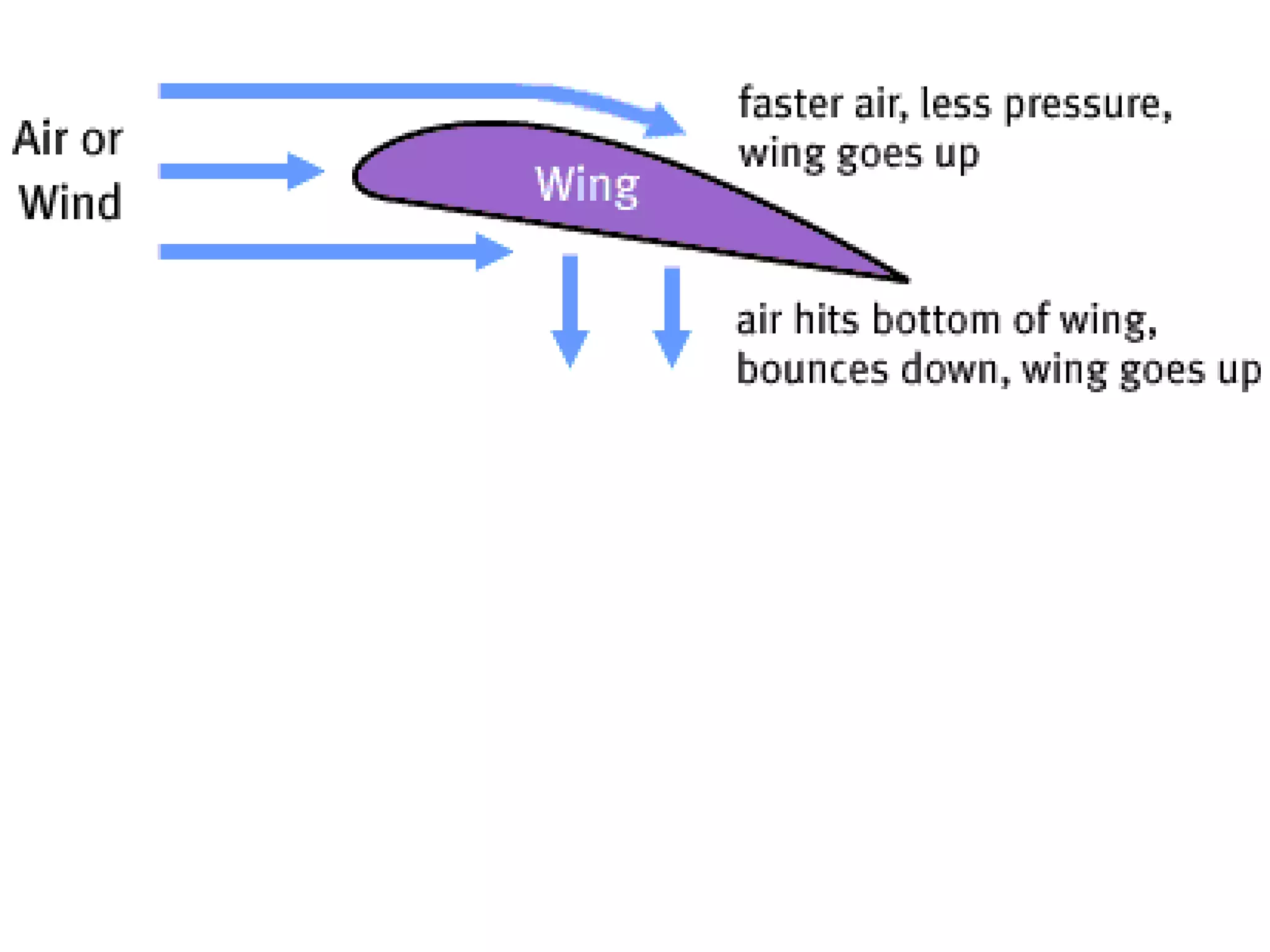
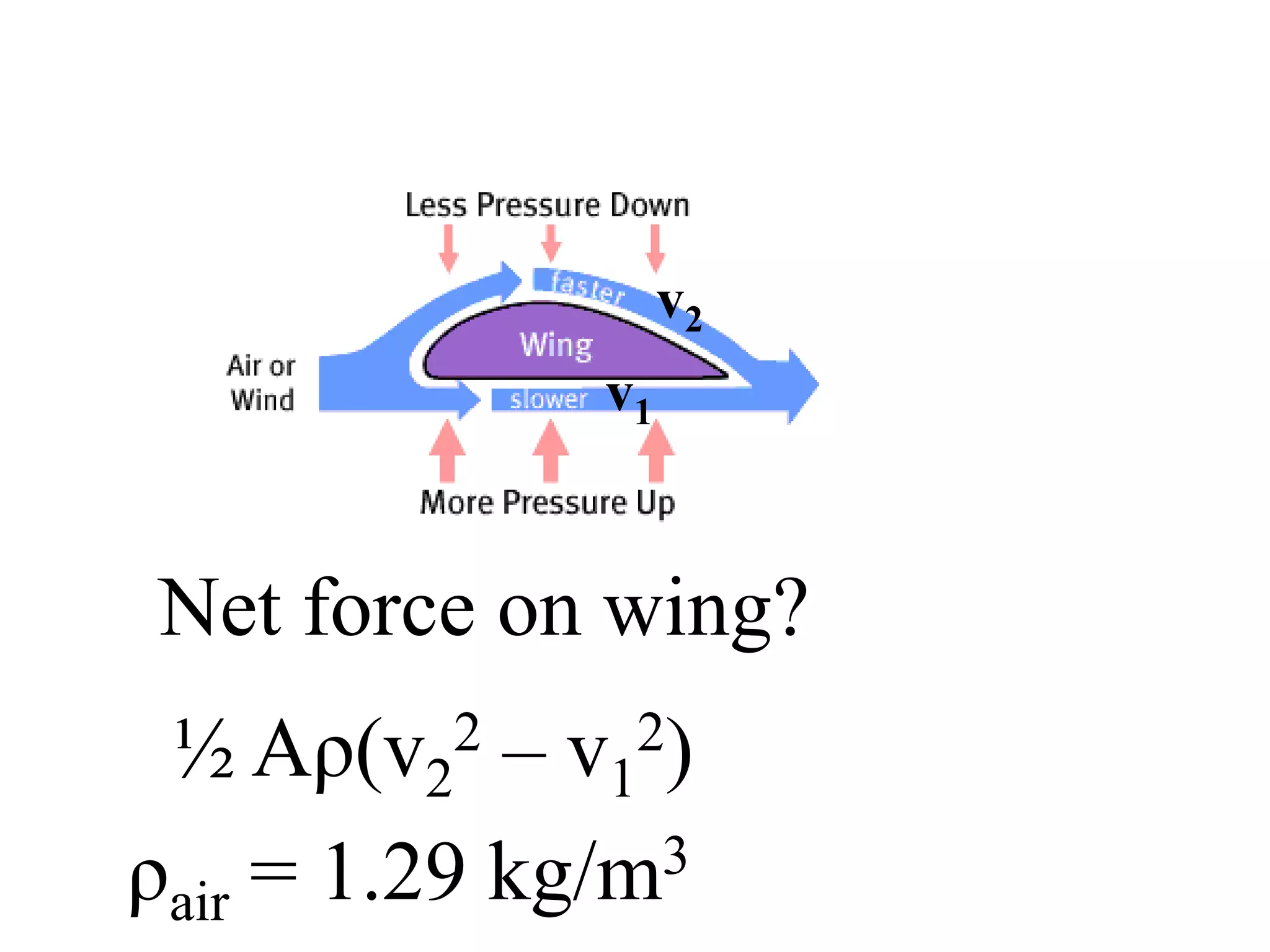
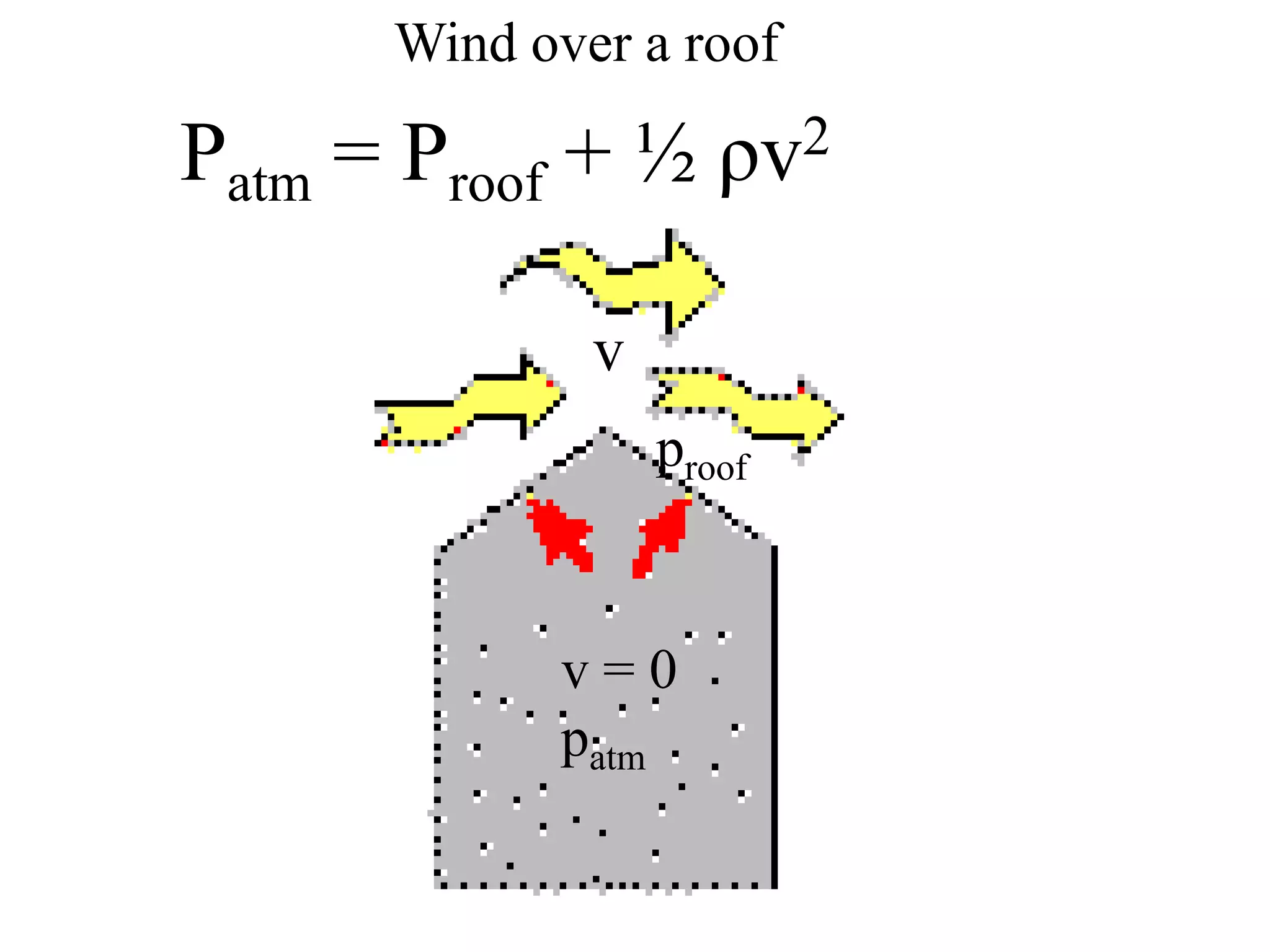
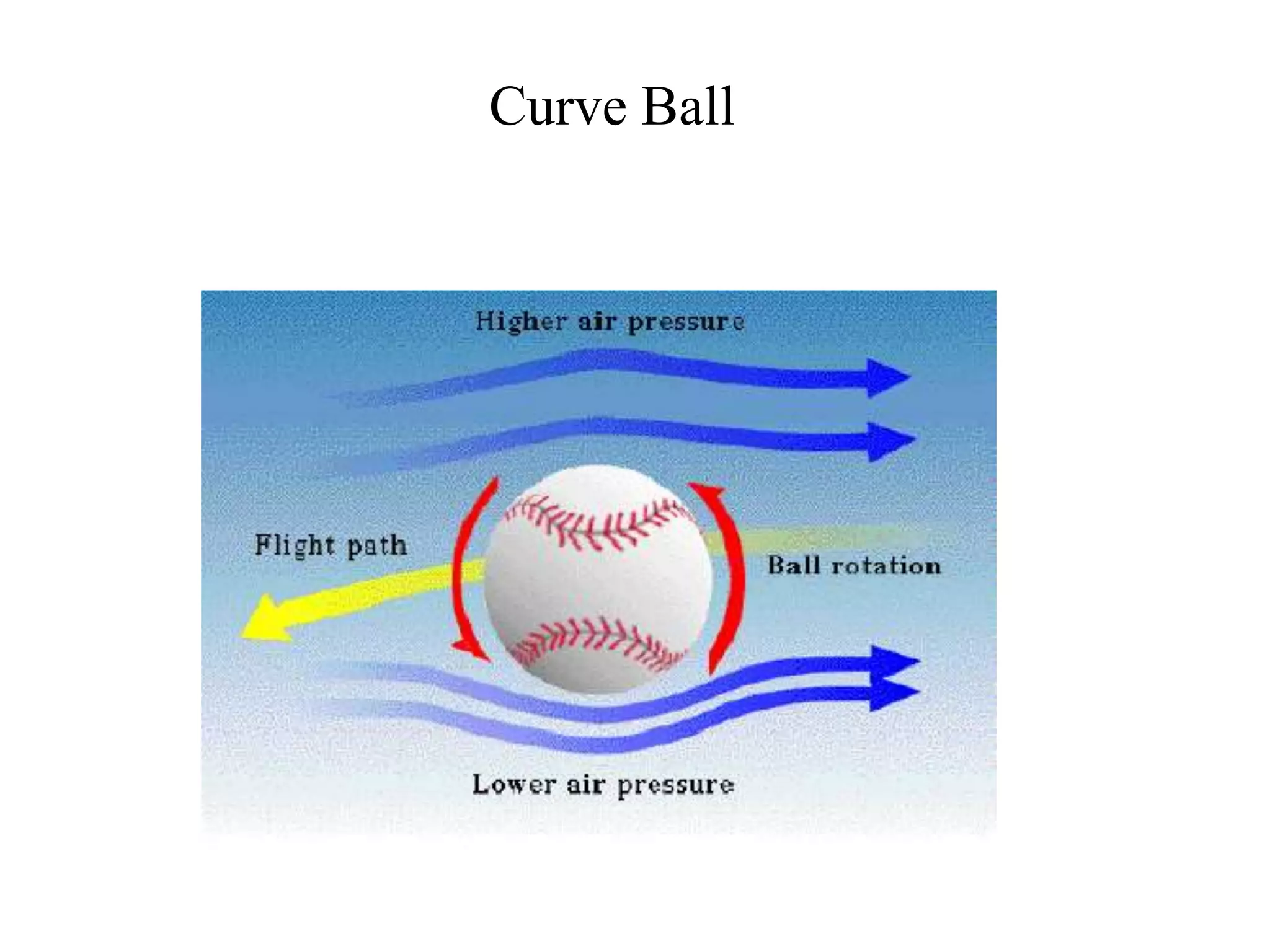
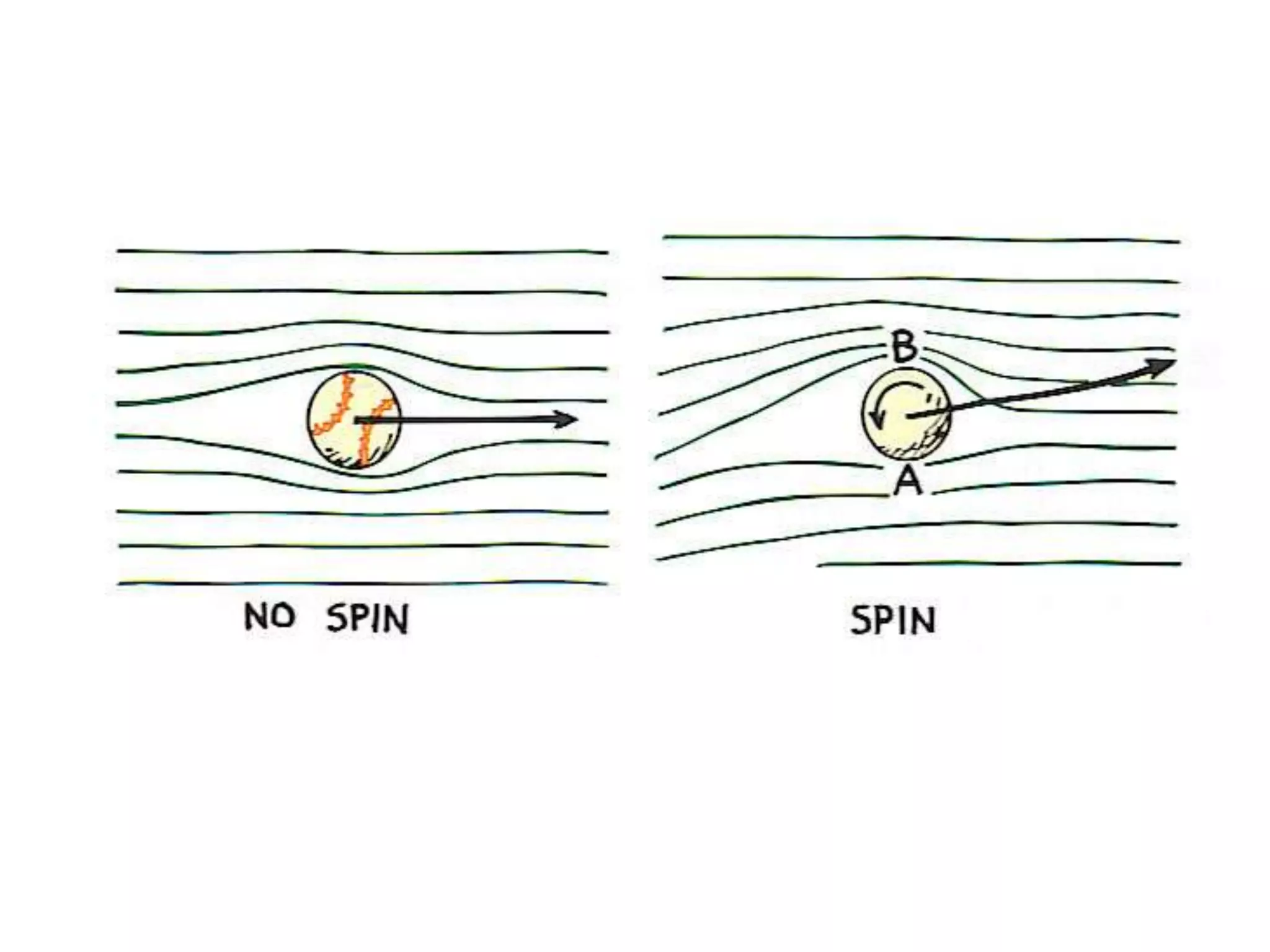
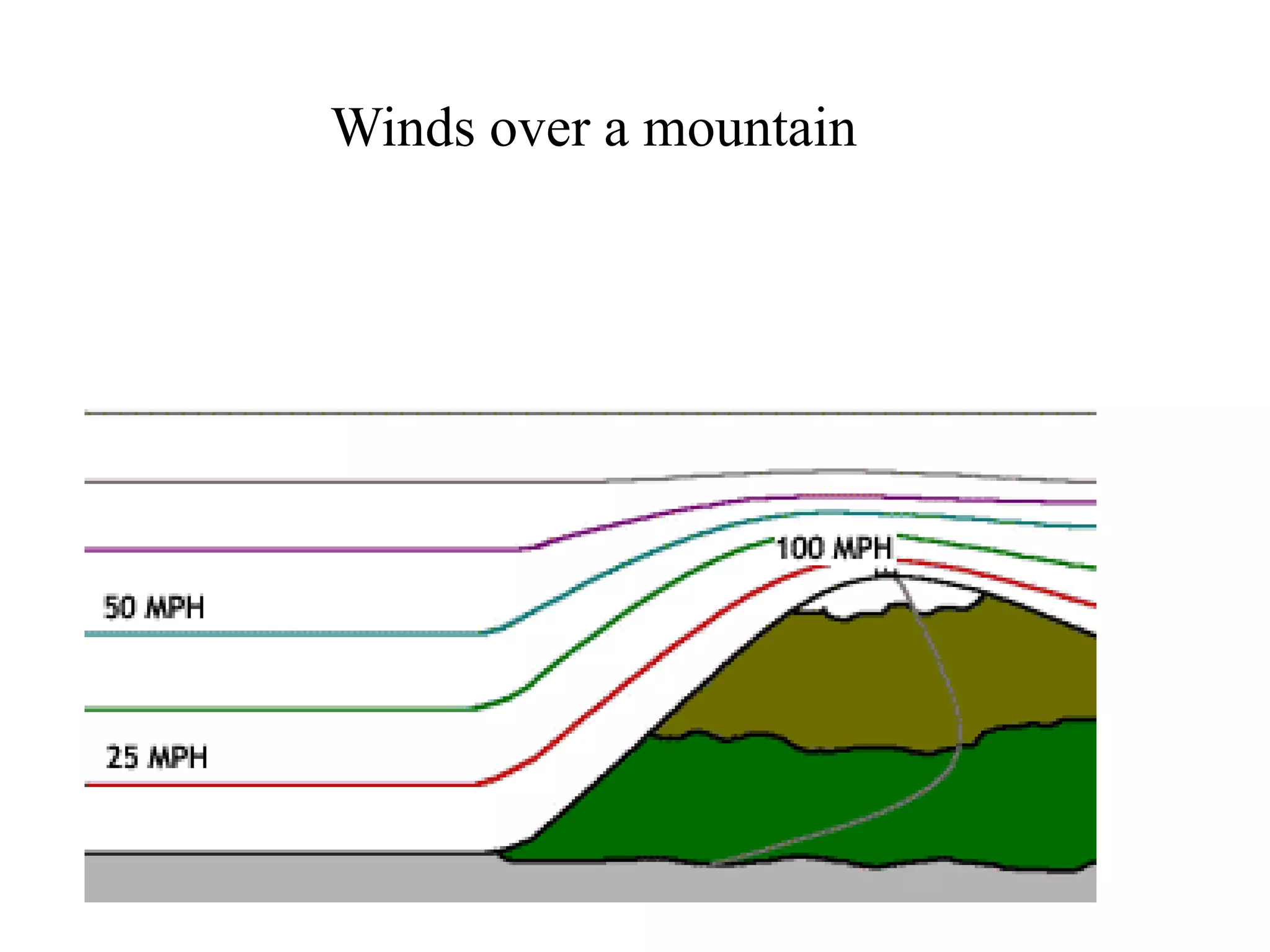
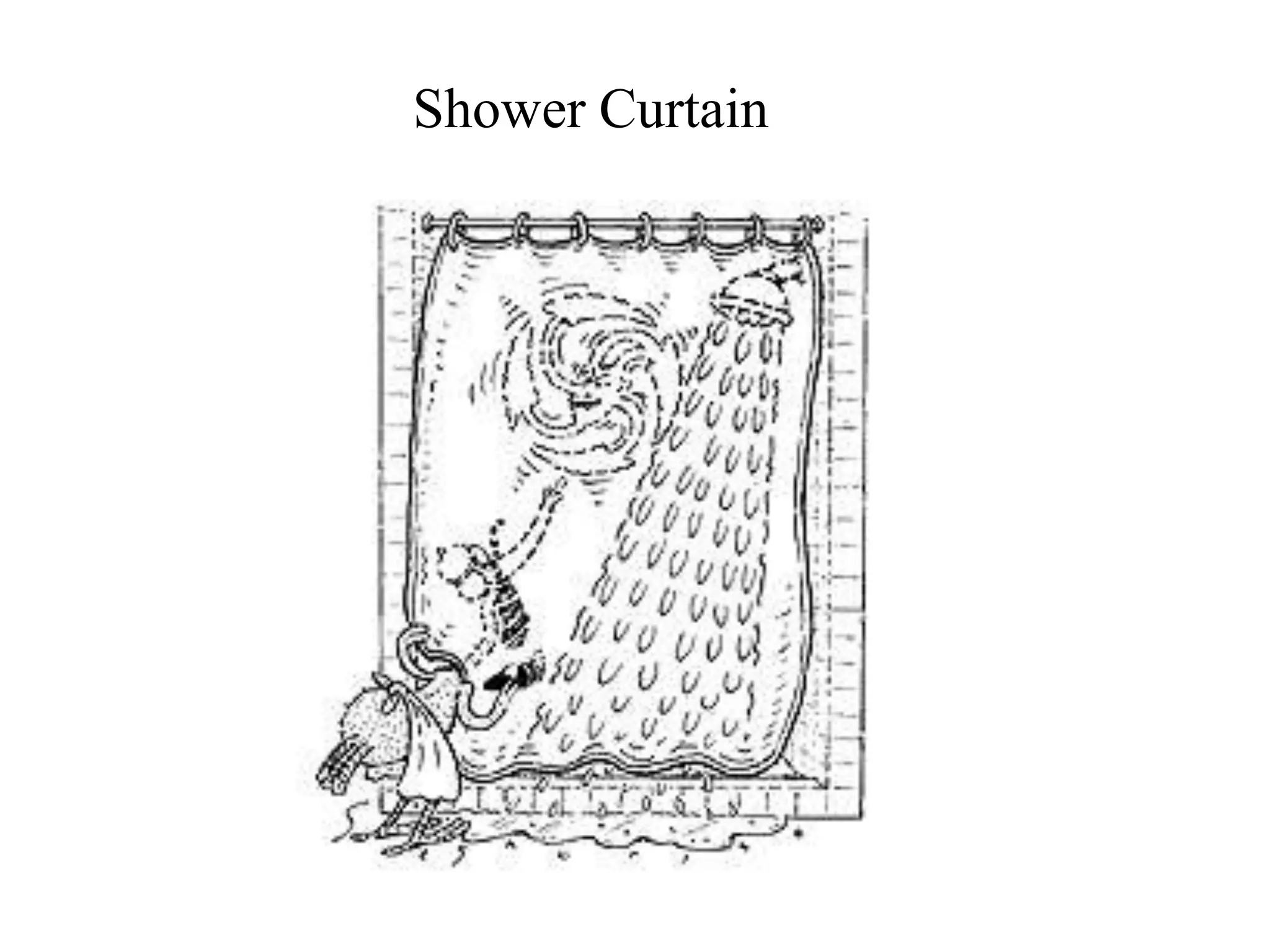
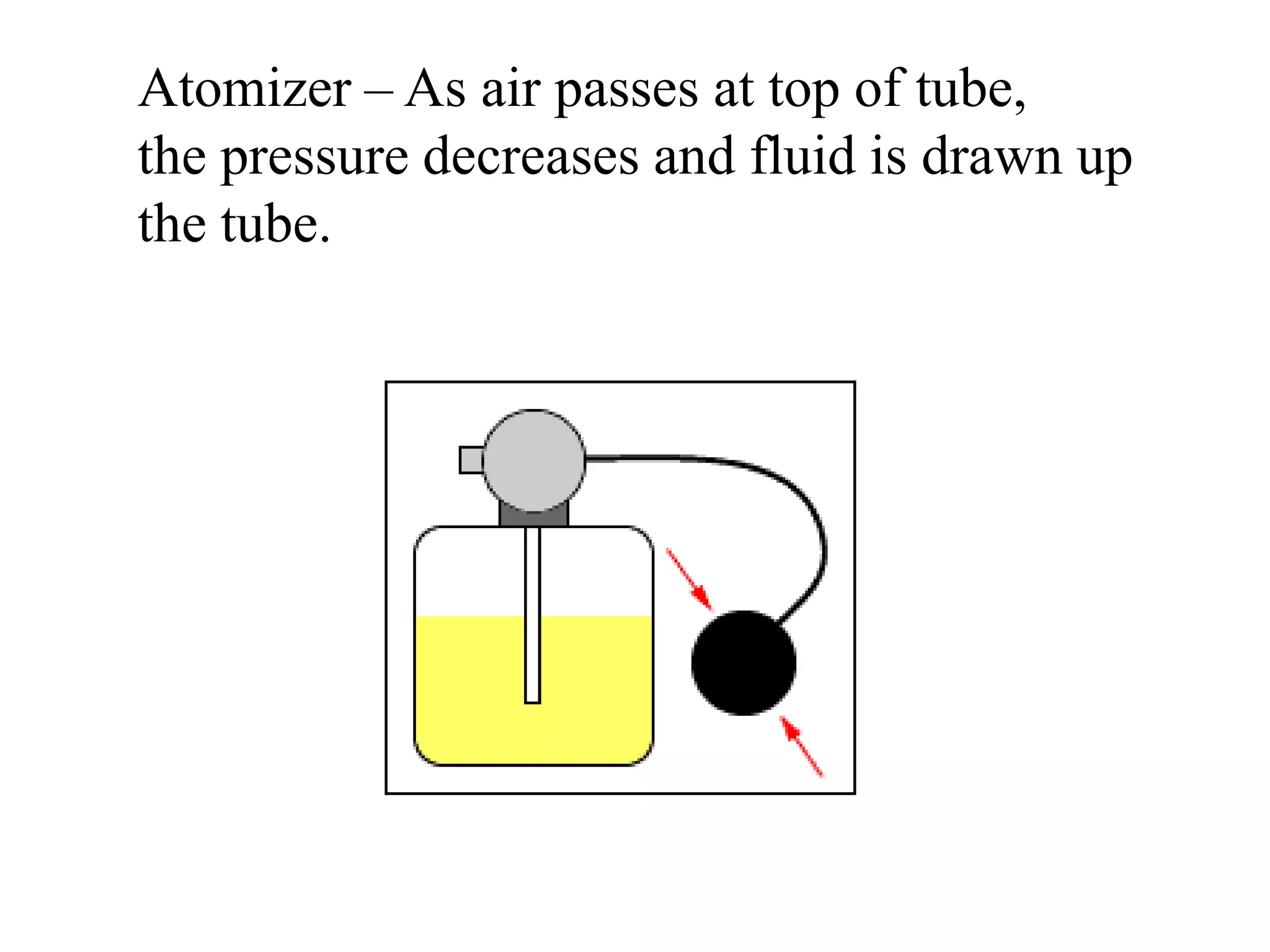
Bernoulli's principle states that as the speed of a fluid increases, the pressure within the fluid decreases. This principle explains how birds and airplanes can fly - the air moves faster over the top of the wing compared to the bottom, creating lower pressure above and higher pressure below, resulting in an upward lift force. It also describes how spoilers on racecars work to provide better traction by creating downward force. Bernoulli's principle is applied in many everyday examples like wind over roofs, curveballs, golf ball dimples, shower curtains, and atomizers.

1. Applications of Bernoulli’s
Principle

2. P+ ρgy + ½
2
ρv
= constant
If no change in height:
P + ½ρv2 = constant
slower speed
faster speed
more pressure
less pressure

3. As the speed of a fluid increases,
the pressure in the fluid decreases.
P α 1/v

4. Motion of fluid
Pressure in fluid
kinetic energy
potential energy
KE + PE is constant

5. d
v
d/4
If incompressible fluid (density = ρ),
change in pressure?

6. Bernoulli & Flight
• Bernoulli’s
Principle is
what allows
birds and
planes to fly.
• The secret
behind flight is
‘under the

8. AIRFOIL
On top: greater air speed and
less air pressure
On bottom: less air speed and
more air pressure

9. LIFT
THRUST
DRAG
GRAVITY

10. v2
v1
Net force on wing?
½ Aρ(v2 – v1
3
ρair = 1.29 kg/m
2
2)

11. Spoiler – airfoil reversed
less air speed
more pressure
greater air speed
less pressure
net force: downward

12. Racecar
Spoiler provides better traction
and avoids lift

13. Wind over a roof
Patm = Proof + ½
2
ρv
v
proof
v=0
patm

14. slow air speed
fast air speed

15. Curve Ball

17. Golf ball dimples

18. Winds over a mountain

19. Shower Curtain

21. Atomizer – As air passes at top of tube,
the pressure decreases and fluid is drawn up
the tube.