Downloaded 1,514 times
Uploaded byEngr.Muhammad Zaroon
Bernoulli's Principle
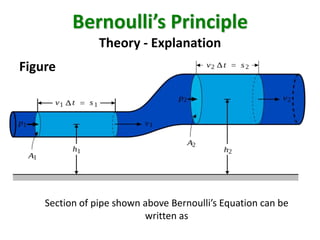
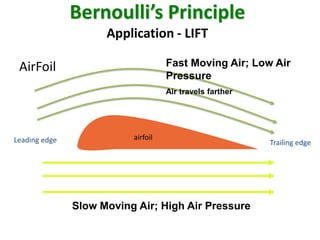
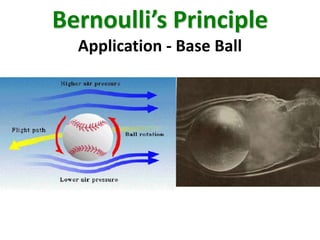
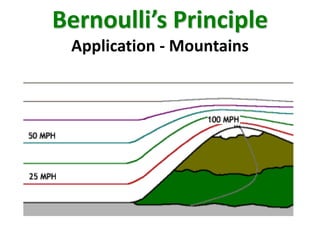
Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in pressure. The principle was introduced by Daniel Bernoulli in 1738 and describes the behavior of incompressible, non-viscous fluids. It explains various phenomena like aircraft lift, spoiler function, tennis ball motion, and carburetor/venturi tube operation. The document covers the theory, equation, and various applications of Bernoulli's principle.
More Related Content
Similar to Bernoulli's Principle
Bernoulli's Principle
- 1. FLUID MECHANICS Presentation Bernoulli’s Principle UmarTariq Husnnain Javeed Adil Faraz Muhammad Zaroon
- 2.
- 3. Bernoulli’s Principle Theory -Introduction Presented by Daniel Bernoulli in his book Hydrodynamica in 1738
- 4. Bernoulli’s Principle Theory -Statement Increase in the speed of the fluid occur simultaneously with a decrease in pressure or a decrease in the fluid's potential energy. OR In a horizontal pipe, the highest fluid pressure is in the section where the flow speed is the lowest, and the lowest pressure is at the section where the flow speed is the biggest. APPLICABLE : INCOMPRESSIBLE - NON VISCOS - NON STEADY
- 5. Bernoulli’s Principle Theory -Explanation Figure Section of pipe shown above Bernoulli’s Equation can be written as
- 6. Bernoulli’s Principle Theory -Equation Where (in SI units) P= static pressure of fluid at the cross section ρ= density of the flowing fluid g= acceleration due to gravity; v= mean velocity of fluid flow at the cross section h= elevation head of the center of the cross section with respect to a datum.
- 7.
- 8.
- 9.
- 10. Bernoulli’s Principle Application -LIFT Fast Moving Air; Low Air Pressure AirFoil Air travels farther Leading edge airfoil Slow Moving Air; High Air Pressure Trailing edge
- 11. Bernoulli’s Principle Application -Spoilers Spoiler provides better stability and avoids lift
- 12. Bernoulli’s Principle Application -Spoilers less air speed more pressure greater air speed less pressure
- 13. Bernoulli’s Principle Application -Tennis Ball
- 14. Bernoulli’s Principle Application -Tennis Ball
- 15. Bernoulli’s Principle Application -Base Ball
- 16. Bernoulli’s Principle Application -Mountains
- 17. Bernoulli’s Principle Application –Ping Pong Ball
- 18.
- 19. Bernoulli’s Principle Application –Carburetor
- 20.
- 21. Bernoulli’s Principle Application –Venturitube • A2 < A1 ; V2 > V1 • According to Bernoulli’s Law, pressure at A2 is lower. • Choked flow: Because pressure cannot be negative, total flow rate will be limited. This is useful in controlling fluid velocity.
- 22. Bernoulli’s Principle Conclusions Aerodynamics Sports RacingIndustry Daily life significance.
- 23.