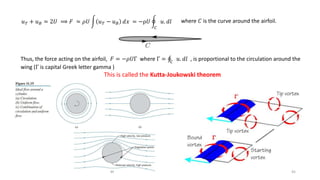
The document provides an overview of topics related to compressible fluid flow, including: - Continuity, impulse-momentum, and energy equations for compressible fluids under isothermal and adiabatic conditions. - Basic thermodynamic relationships like the ideal gas law, processes like isothermal and adiabatic, and concepts like internal energy and entropy. - Propagation of elastic waves in fluids due to compression, and how the velocity of sound depends on factors like pressure, temperature, and fluid properties. - Additional topics covered include stagnation properties, flow through converging-diverging passages, shock waves, and external aerodynamic flows.

1. Greetings, dear viewers
Name & ID of the presenter :
Razin Sazzad Molla 13107010
13107010@iubat.edu
razin505@gmail.com
1

2. Topics to be covered
Compressible flow of fluids, Introduction of thermodynamics to the study
of compressible fluids, Continuity equation, Impulse momentum
equation, Energy equation for isothermal & adiabatic condition,
Propagation of elastic wave, velocity of sound, Mach number its
significance, Stagnation point& pressure, Flow of compressible fluid with
negligible friction through a pipe of varying cross section, Flow through
convergent divergent passages, Shock waves, Measurement of
compressible fluid flow, Fluid flow around submerged objects (external
flow), Drag & lift, Types of drag, Drag coefficients of general geometry,
generation of lift, Airfoil theory, Drag & lift on airfoils, Induced drag on an
airfoil of finite length, Design of wings, Streamlined body
2

3. Compressible fluid
In general all the fluids are compressible, but in any fluid flow if the density of the fluid
does not change appreciably then the fluid may be treated as incompressible. However
when the density changes are appreciable the compressibility of the fluid needs to be
taken into account in the analysis of such fluid phenomena. Significant density changes
may usually be produced in a gas if the velocity (either of the gas itself or of a body moving
through it) approaches or exceeds the speed of propagation of sound through the gas, if
the gas is subjected to sudden acceleration or if there are very large change in elevation.
Compressible flow combines fluid dynamics and thermodynamics in that both are
necessary to the development of the required theoretical background.
Basic relationships of thermodynamics
When the physical properties of a gas such as pressure
density& temperature are changed due to compression or
expansion of the gas it is said to undergo a process. A gas may
be compressed or expanded either by isothermal process or
adiabatic process. An isothermal process is that in which the
temperature is held constant and is governed by Boyle’s law
𝑝𝑣 = 𝑝1 𝑣1 = 𝑝2 𝑣2=constant
𝑝/𝜌 = 𝑝1/𝜌1 = 𝑝2/𝜌2 =constant
𝑝/𝑤 = 𝑝1/𝑤1 = 𝑝2/𝑤2 =constant
During an adiabatic process the gas neither absorbs
heat from, nor gives heat to its surroundings
𝑝𝑣 𝑘
= 𝑝1 𝑣1
𝑘
= 𝑝2 𝑣2
𝑘
=constant
𝑝/𝜌 𝑘 = 𝑝1/𝜌1
𝑘
= 𝑝2/𝜌2
𝑘
=constant
𝑝/𝑤 𝑘 = 𝑝1/𝑤1
𝑘
= 𝑝2/𝑤2
𝑘
=constantIn the above equations:
𝑝 =pressure, 𝑣 =specific volume, 𝜌 = mass density,
𝑤=weight density,k=adiabatic heat index (𝑐 𝑝
/𝑐 𝑣
) 3

4. The process is said to be reversible if the gas and its surroundings could subsequently be
completely restored to their initial conditions by adding to (or extracting from)the gas exactly
the same amount of heat & work taken from (or added to)it during the process. A frictionless
adiabatic process is a reversible process and often called isentropic process as the entropy
remains constant. However a reversible process is merely hypothetical/ideal(never achieved in
real practice)
Equation of state: The density 𝜌 of a particular gas is related to its absolute pressure 𝑝 and
absolute temperature 𝑇 by the equation of state which for a perfect gas takes the form 𝑝 =
𝜌𝑅𝑇 or 𝑝𝑉 = 𝑚𝑅𝑇 in which 𝑅 is gas constant and 𝑉 is the volume occupied by the mass 𝑚 of
the gas.
Internal energy: the energy possessed by the molecules of a fluid due to intermolecular
activity. Its distinguished from external energies (kinetic and potential energy). It can not be
measured directly but manifests itself in terms of temperature
4

5. First law of thermodynamics
It states that:
Heat and mechanical work are mutually convertible. According to this law when a closed system
undergoes a thermodynamic cycle the net heat transfer is equal to the net work transfer. Mathematically,
𝛿𝑄 = 𝛿𝑊
When a system undergoes a change of state (or a thermodynamic process)then both heat transfer &work
transfer takes place. The net energy transfer is stored within the system and is known as stored energy or
total energy of the system. Mathematically,
𝛿𝑄 − 𝛿𝑊 = 𝑑𝐸 / TdS − pdV = ∆𝐸
For isothermal process since the temperature remains constant 𝛿𝑄 = 0 so, 𝛿𝑊 + 𝑑𝐸 = 0
The work done by a gas in expanding(or on a gas in contracting)is given by,
𝑊 = 𝑣1
𝑣2
𝑝𝑑𝑉
Integrating this equation we obtain the equations of work done for isothermal and adiabatic processes.
𝑊 = 𝑝1 𝑣1 log 𝑒
𝑣2
𝑣1
= 𝑝1 𝑣1 log 𝑒
𝑝1
𝑝2
5

6. Or, 𝑊 = 𝐾 log 𝑒
𝑣2
𝑣1
= 𝐾 log 𝑒
𝑝1
𝑝2
in which 𝐾 is the constant from Boyle’s equation.
Similarly for adiabatic process ,
𝑊 =
1
𝑘 − 1
(𝑝1 𝑣1 − 𝑝2 𝑣2)
Entropy:
Entropy of a gas may be defined as the measure of the maximum heat energy available
for conversion into work.it is a property of the gas and it varies with its absolute
temperature and its state. 𝛿𝑄 = 𝑇𝑑𝑆
Where, 𝑇 =absolute temperature
𝑑𝑆 =increase in entropy
6

7. Continuity Equation
The continuity equation is actually
mathematical statement of the principle
of conservation of mass which states
that mass can neither be destroyed nor
be created
Continuity equation in Cartesian
coordinates: Consider an elementary rectangular parallelepiped with sides of length
𝛿𝑥, 𝛿𝑦 & 𝛿𝑧 as shown in figure. Let the center of the parallelepiped be at a point
𝑃(𝑥, 𝑦, 𝑧) where the velocity components in the 𝑥, 𝑦, 𝑧 directions are 𝑢, 𝑣 & 𝑤
respectively and 𝜌 be the mass density of the fluid. The continuity equation is
obtained as
𝜕𝜌
𝜕𝑡
+
𝜕 𝜌𝑢
𝜕𝑥
+
𝜕 𝜌𝑣
𝜕𝑦
+
𝜕 𝜌𝑤
𝜕𝑧
= 0 this equation represents
the continuity equation in its most general from and is applicable for steady
/unsteady/uniform/non-uniform/incompressible/compressible
multidimensional flows. In vector notation the continuity equation may be
expressed as
𝐷𝜌
𝐷𝑡
+ ρ𝛻. 𝑉 = 0 in which
𝐷𝜌
𝐷𝑡
=
𝜕𝜌
𝜕𝑡
+ 𝑢
𝜕𝜌
𝜕𝑥
+
𝜕𝜌
𝜕𝑦
+
𝜕𝜌
𝜕𝑧
and 𝛻. 𝑉 = div𝑉 =
𝜕𝑢
𝜕𝑥
+
𝜕𝑣
𝜕𝑦
+
𝜕𝑤
𝜕𝑧
7

8. Continuity Equation for one dimensional flow
Consider a tube shaped elementary parallelepiped along a
stream-tube of length 𝛿𝑠 as shown in figure. Since the flow
through a stream-tube is always along the tangential direction
there is no component of velocity in the normal direction. If at
the central section of the elementary stream-tube ,𝐴 is the
cross sectional area, 𝑉 is the mean velocity of flow, 𝜌 is the
mass density of the fluid then the mass of fluid passing this
section per unit time is equal to 𝜌𝐴𝑉
The mass of fluid entering the tube per unit time at section
𝑁𝑀 = [𝜌𝐴𝑉 −
𝜕
𝜕𝑠
(𝜌𝐴𝑉)
𝛿𝑠
2
]
Similarly the mass of fluid leaving the tube per unit
time at section 𝑁′ 𝑀′ = [𝜌𝐴𝑉 +
𝜕
𝜕𝑠
(𝜌𝐴𝑉)
𝛿𝑠
2
]
Therefore the net mass of fluid that has remained
per unit time= −
𝜕
𝜕𝑠
(𝜌𝐴𝑉) 𝛿𝑠 The mass of fluid in
the tube = 𝜌𝐴 𝛿𝑠 and its rate of increase with time
=
𝜕
𝜕𝑡
𝜌𝐴 𝛿𝑠 =
𝜕
𝜕𝑡
𝜌𝐴 𝛿𝑠 8

9. Since the net mass of fluid that has remained in the parallelepiped per unit time is equal to
the rate of increase of mass with time ,
−
𝜕
𝜕𝑠
(𝜌𝐴𝑉) 𝛿𝑠 =
𝜕
𝜕𝑡
𝜌𝐴 𝛿𝑠
Dividing both sides of the above expression by 𝛿𝑠 and taking the limit so as to reduce the
parallelepiped to a point the continuity equation is obtained as
𝜕
𝜕𝑡
𝜌𝐴 +
𝜕
𝜕𝑠
𝜌𝐴𝑉 = 0
This equation represents continuity equation for one dimensional flow in a most general
form which will be applicable for steady or unsteady flow, uniform od non-uniform flow and
for compressible fluids.
For steady flow as there’s no variation with respect to time the equation reduces to :
𝜕
𝜕𝑠
𝜌𝐴𝑉 = 0
From which we obtain:
𝜌𝐴𝑉 = constant
𝜌𝐴𝑉 = 𝜌1 𝐴1 𝑉1 = 𝜌2 𝐴2 𝑉2=constant
9

10. Impulse momentum equation
The impulse momentum equations are derived from the
impulse momentum principle or simply momentum principle
which states that the impulse exerted on any body is equal to
the resulting change in momentum of the body. Thus for an
arbitrarily chosen direction 𝑥 it maybe expressed as :
𝐹𝑥 =
𝑑(𝑀 𝑥)
𝑑𝑡
in which 𝐹𝑥 represents the resultant external force
and 𝑀 𝑥 represents the momentum in the 𝑥 direction.
𝐹𝑥 =
𝐴2
𝜌2 𝑣2 𝑑𝑡 𝑑𝐴2 (𝑉2) 𝑥−
𝐴1
𝜌1 𝑣1 𝑑𝑡 𝑑𝐴1(𝑉1) 𝑥
Where 𝜌2 𝑣2 𝑑𝑡𝑑𝐴2 and 𝜌1 𝑣1 𝑑𝑡𝑑𝐴1 represent the mass of flow
of fluid during the time interval 𝑑𝑡 in a stream tube across
section 2-2 and 1-1 as shown in figure
To simplify the equation becomes:
𝐹𝑥 = (𝜌𝐴𝑉𝑉𝑥)2−(𝜌𝐴𝑉𝑉𝑥)1
10

11. Energy Equation
The total energy 𝐸1at a point in a compressible fluid flow system comprises the following:
1. Kinetic energy 𝐸 𝑘
2. Potential energy 𝐸𝑒
3. Flow or pressure energy 𝐸 𝑝
4. Molecular energy 𝐸 𝑚
This maybe expressed as 𝐸𝑡 = 𝐸 𝑘 + 𝐸𝑒 + 𝐸 𝑝 + 𝐸 𝑚
According to the law of conservation of energy the total energy at one point in a fluid flow system
plus the energy added 𝐸 𝑎 minus the energy subtracted 𝐸𝑠 between two points must be equal to
the total energy at the second point in the system. That is (𝐸 𝑘 + 𝐸𝑒 + 𝐸 𝑝 + 𝐸 𝑚)1+𝐸 𝑎 − 𝐸𝑠 =
𝐸 𝑘 + 𝐸𝑒 + 𝐸 𝑝 + 𝐸 𝑚 2
… … … … (1)
This equation shows that energy can neither be created nor be destroyed but can be changed from
one from to another on the two sides of the equation but the total number must be same.
Equation (1) can be written in terms of energy per unit weight of the following fluid as
(
𝑣2
2𝑔
+ 𝑧 + 𝐸 𝑛)1+(𝐸 𝑛-𝐸𝑠) = (
𝑣2
2𝑔
+ 𝑧 + 𝐸 𝑛)2 in which
𝑣2
2𝑔
is kinetic energy, 𝑧 is potential energy and
𝐸 𝑛 is enthalpy each of these being per unit weight of the fluid.
11

12. In the case of isothermal flow since the temperature remains constant so 𝐸1 =
𝐸2 and we know 𝑝1/𝑤1 = 𝑝2/𝑤2 therefore 𝐸 𝑛1 = 𝐸 𝑛2. Further 𝐸 𝑎 is usually
the heat energy 𝐻,which for isothermal flow is equal to the work done. Now if
there is no loss of energy (𝐸𝑠= 0) then for a frictionless isothermal flow of fluid
the energy equation becomes 𝐾 log 𝑒
𝑝1
𝑝2
=
𝑣2
2
2𝑔
−
𝑣1
2
2𝑔
+ (𝑧2 − 𝑧1)
In the case of adiabatic flow there being neither removal nor addition of heat
energy 𝐸 𝑎 = 𝐻 = 0 and we know work done 𝑊 =
1
𝑘−1
(
𝑝1
𝑤1
−
𝑝2
𝑤 2
) thus for
this case 𝐸 𝑛1 − 𝐸 𝑛2 =
𝑘
𝑘−1
(
𝑝1
𝑤1
−
𝑝2
𝑤 2
) again if there is no loss of energy 𝐸𝑠 =
0, then for a frictionless adiabatic flow of fluid the energy equation becomes
𝑘
𝑘−1
𝑝1
𝑤1
−
𝑝2
𝑤 2
=
𝑣2
2
2𝑔
−
𝑣1
2
2𝑔
+ (𝑧2 − 𝑧1)
12

13. Propagation of elastic waves due to
compression of fluid, velocity of sound
If the pressure at a point in a fluid is changed the new pressure is rapidly transmitted
throughout the rest of the fluid is so happens because any change in pressure causes an
elastic or pressure wave reflecting this change to travel through the fluid at a certain
velocity. In a completely incompressible fluid the transmission of new pressure would take
place instantaneously and hence the elastic or pressure wave would be propagated with
infinite velocity. However in a compressible fluid the elastic or pressure wave is
propagated with finite velocity but even in a compressible fluid the changes of pressure
are transmitted quite rapidly and as indicated ,the velocity of propagation of the elastic
wave in a compressible fluid is equal to the velocity of sound in that fluid medium
13

14. Consider a long rigid tube of uniform cross sectional area 𝐴 fitted with a piston at one end as
shown in figure. The tube is filled with a compressible fluid initially at rest. If the piston is
moved suddenly to the right with a velocity 𝑣 𝑝 a pressure wave would be propagated
through the fluid at a velocity 𝐶. During a small time interval 𝑑𝑡 the piston moves through a
distance 𝑑𝑥 = (𝑣 𝑝 𝑑𝑡) while the pressure wave travels ahead of the piston through a distance
𝑑𝐿 = (𝐶𝑑𝑡)
14

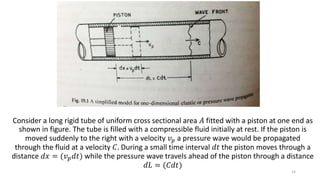
15. Before the sudden motion of the piston the fluid within the length 𝑑𝐿 has an initial
density 𝜌 and its total mass is (𝜌 𝑑𝐿 𝐴) .after the piston is moved through a distance 𝑑𝑥
the fluid density within the compressed region of length (𝑑𝐿 − 𝑑𝑥) will be increased and
becomes (𝜌 + 𝑑𝜌). Thus the total mass of fluid in the compressed region will be [(𝜌 +
𝑑𝜌) 𝑑𝐿 − 𝑑𝑥 𝐴] therefore according to the principle of continuity 𝜌 (𝑑𝐿) 𝐴 = (𝜌 + 𝑑𝜌)
𝑑𝐿 − 𝑑𝑥 𝐴
Or, 𝜌 (𝑑𝐿) =(𝜌 + 𝑑𝜌) 𝑑𝐿 − 𝑑𝑥
But 𝑑𝐿 = Cdt and 𝑑𝑥 = 𝑣 𝑝 𝑑𝑡 the above equation becomes,
𝜌 (𝐶𝑑𝑡) =(𝜌 + 𝑑𝜌) 𝐶 − 𝑣 𝑝 𝑑𝑡
Or, 0 = Cd𝜌 − 𝜌𝑣 𝑝 − 𝑑𝜌𝑣 𝑝
Since the velocity 𝑣 𝑝 of the piston is much smaller than the elastic wave velocity 𝐶 the
term 𝑑𝜌𝑣 𝑝 maybe neglected and hence 𝐶 𝑑𝜌 = 𝜌𝑣 𝑝 or 𝐶 =
𝜌𝑣 𝑝
𝑑𝜌
………………….(1)
15

16. Further in the region of compressed fluid the fluid particles have acquired velocity which
is apparently equal to the velocity of the piston accompanied by an increase in pressure
𝑑𝑝 due to the sudden motion of the piston. Thus applying the impulse momentum
equation for the fluid in the compressed region during 𝑑𝑡, we get
𝑑𝑝𝐴𝑑𝑡 = 𝜌𝑑𝐿𝐴(𝑣 𝑝−0)
Which maybe simplified as, 𝑑𝑝 = 𝜌
𝑑𝐿
𝑑𝑡
× 𝑣 𝑝 = 𝜌𝐶𝑣 𝑝
Since 𝑑𝐿 = 𝐶𝑑𝑡
Thus 𝐶 =
𝑑𝑝
𝜌𝑣 𝑝
……………….(2)
By combining equations 1&2 𝑐2 =
𝑑𝑝
𝑑𝜌
Or, 𝐶 =
𝑑𝑝
𝑑𝜌
………………..(3)
Thus the velocity of propagation of elastic or pressure wave in a compressible fluid is
given by this equation.
16

17. Again we know that bulk modulus of elasticity of fluid is defined as 𝐾 = −
𝑑𝑝
𝑑𝑣/𝑣
Since volume 𝑣 ∝
1
𝜌
or 𝑣𝜌 =constant
Differentiating both sides we get 𝑣𝑑𝜌 + 𝜌𝑑𝑣 = 0
𝑑𝑣
𝑣
= −
𝑑𝜌
𝜌
So, 𝐾 = −
𝑑𝑝
𝑑𝜌/𝜌
……….(4)
Putting this value to the e𝑞 𝑛 3 we get,
𝐶 =
𝐾
𝜌
This equation shows that velocity of elastic or pressure wave depends on the bulk modulus
of elasticity and the density of the fluid in which it is propagated. Furthermore the velocity
of sound (which is also composed of elastic waves of this nature) in any fluid medium is
also equal to
𝐾
𝜌
17

18. For isothermal process we know that
𝑝
𝜌
=constant
Or,
𝑑𝑝
𝜌
−
𝑝𝑑𝜌
𝜌2 = 0
Or,
𝑑𝑝
𝑑𝜌
=
𝑝
𝜌
………….(5)
From equation 4&5 we get for isothermal process 𝐾 = 𝑝 so we can write,
𝐶 =
𝑝
𝜌
= 𝑅𝑇
Since for perfect gas from the equation of state 𝑝 = 𝜌𝑅𝑇
18

19. Similarly for isentropic process we know
𝑝
𝜌 𝑘 =constant
Or,
𝑑𝑝
𝜌 𝑘 −
𝑘𝑝𝑑𝜌
𝜌 𝑘+1 = 0
Or,
𝑑𝑝
𝑑𝜌
=
𝑘𝑝
𝜌
…………….(6)
From equation 4&6 we get , 𝐾 = 𝑘𝑝
So we can write 𝐶 = (𝑘𝑝/𝜌) = 𝑘𝑅𝑇
19

20. Mach number and its significance
The Mach number Ma (or 𝑁 𝑀) at a point in the flow is defined as the ratio of velocity 𝑉 of flow at the point to
the velocity of sound or sonic velocity 𝐶 in that fluid medium corresponding to the values of 𝐾 and 𝜌 existing
at the point where 𝑉 is measured that is,
𝑀𝑎 =
𝑉
𝐶
The Mach number is a dimensionless parameter which is the square root of the ratio of inertia force of the
flow to the elastic force of fluid. Therefore for two geometrically similar compressible flow systems the
dynamic similarity can be obtained when the ratio (𝑉/𝐶) or 𝑀𝑎 is a constant for corresponding points in two
systems. Further it maybe mentioned that Mach number is important in those problems in which the velocity
of flow is comparable with the velocity of sound or sonic velocity. It may happen in the case of airplanes
travelling at very high speed, bullets ,projectiles etc. however if for any flow system the Mach number is less
than about 0.4 the effect of compressibility may be neglected for that flow system. Depending on the value of
Mach number the flow can be classified as follows,
Subsonic flow : 𝑀𝑎 < 1
Sonic flow : 𝑀𝑎 = 1
Supersonic flow : 1 < 𝑀𝑎 < 3
Hypersonic flow : 𝑀𝑎 > 4
When the mach number in a flow region is slightly less to slightly greater than unity , the flow is termed as
transonic flow.
20

21. Categories of compressible flow
we learned that the effects of
compressibility become more significant
as the Mach number increases. we can
conclude that incompressible flows can
only occur at low Mach numbers.
Experience has also demonstrated that
compressibility can have a large
influence on other important flow
variables. For example, in Fig. 11.2 the
variation of drag coefficient with
Reynolds number and Mach number is
shown for air flow over a sphere.
Compressibility effects can be of
considerable importance.
21

22. To further illustrate some curious features of compressible flow, a simplified example is
considered. Imagine the emission of weak pressure pulses from a point source. These pressure
waves are spherical and expand radially outward from the point source at the speed of sound,
c. If a pressure wave is emitted at different times, we can determine where several waves will
be at a common instant of time, t, by using the relationship
𝑟 = 𝑡 − 𝑡 𝑤𝑎𝑣𝑒 𝑐
where r is the radius of the sphere-shaped wave emitted at time For a stationary point source,
the symmetrical wave pattern shown in Fig. 11.3a is involved.
22

23. 23

24. When the point source moves to the left with a constant velocity, V, the wave pattern is no
longer symmetrical. In Figs. 11.3b, 11.3c, and 11.3d are illustrated the wave patterns at s for
different values of Also shown with a “ ” are the positions of the moving point source at values of
time, t, equal to 0 s, 1 s, 2 s, and 3 s. Knowing where the point source has been at different
instances is important because it indicates to us where the different waves originated.
From the pressure wave patterns of Fig. 11.3, we can draw some useful conclusions.
When the point source and the fluid are stationary, the pressure wave pattern is symmetrical (Fig.
11.3a) and an observer anywhere in the pressure field would hear the same sound frequency from
the point source.
When the point source moves in fluid at rest (or when fluid moves past a stationary point source),
the pressure wave patterns vary in asymmetry, with the extent of asymmetry depending on the
ratio of the point source (or fluid) velocity and the speed of sound. When 𝑉/𝑐 < 1 the wave pattern
is similar to the one shown in Fig. 11.3b. This flow is considered subsonic and compressible. A
stationary observer will hear a different sound frequency coming from the point source depending
on where the observer is relative to the source because the wave pattern is symmetrical.
24

25. When (
𝑉
𝑐
= 1) pressure waves are not present ahead of the moving point source. The
flow is sonic. If you were positioned to the left of the moving point source, you would
not hear the point source until it was coincident with your location. For flow moving past
a stationary point source at the speed of sound (
𝑉
𝑐
= 1) the pressure waves are all
tangent to a plane that is perpendicular to the flow and that passes through the point
source. The concentration of pressure waves in this tangent plane suggests the
formation of a significant pressure variation across the plane. This plane is often called a
Mach wave. Note that communication of pressure information is restricted to the region
of flow downstream of the Mach wave. The region of flow upstream of the Mach wave is
called the zone of silence and the region of flow downstream of the tangent plane is
called the zone of action.
25

26. When 𝑉 > 𝑐 the flow is supersonic and the pressure wave pattern resembles the one depicted in Fig.
11.3d. A cone (Mach cone) that is tangent to the pressure waves can be constructed to represent the
Mach wave that separates the zone of silence from the zone of action in this case. The communication
of pressure information is restricted to the zone of action. From the sketch of Fig. 11.3d, we can see
that the angle of this cone 𝛼, is given by
sin 𝛼 =
𝑐
𝑉
=
1
𝑀𝑎
This discussion about pressure wave patterns suggests the following categories of fluid flow:
1. Incompressible flow: 𝑀𝑎 ≤ 0.3 Unrestricted, nearly symmetrical and instantaneous pressure
communication.
2. Compressible subsonic flow: 0.3 < 𝑀𝑎 < 1.0 Unrestricted but noticeably asymmetrical
pressure communication.
3. Compressible supersonic flow: 𝑀𝑎 ≥ 1.0 Formation of Mach wave; pressure communication
restricted to zone of action.
In addition to the above-mentioned categories of flows, two other regimes are commonly referred to:
namely, transonic flows (0.9 ≤ 𝑀𝑎 ≤ 1.2) and hypersonic flows (𝑀𝑎 > 5).
Modern aircraft are mainly powered by gas turbine engines that involve transonic flows. When a space
shuttle reenters the earth’s atmosphere, the flow is hypersonic. Future aircraft may be expected to
operate from subsonic to hypersonic flow conditions.
26

27. Sonic boom
A sonic boom is the sound associated with the shock waves created by an object traveling through the air
faster than the speed of sound. Sonic booms generate enormous amounts of sound energy, sounding
much like an explosion. The crack of a supersonic bullet passing overhead or the crack of a bullwhip are
examples of sonic boom in miniature
The sound source is traveling at 1.4
times the speed of sound(𝑀𝑎 1.4).
Since the source is moving faster
than the sound waves it creates, it
leads the advancing wavefront.
A sonic boom produced by an aircraft moving at 𝑀𝑎 = 2.92 calculated
from the cone angle of 20 degrees. An observer hears nothing until the
shock wave on the edges of the cone crosses their location. 27

28. Sonic boom created by US navy
fighter jet F/A-18F super hornet
which has a top speed of 1190 mph
F-14 Tomcat breaking the sound
barrier over water
28

29. STAGNATION PROPERTIES
When analyzing control volumes, we find it very convenient to combine the
internal energy and the flow energy of a fluid into a single term, enthalpy,
defined per unit mass as ℎ = 𝑢 + 𝑝/𝜌. Whenever the kinetic and potential energies of the fluid are
negligible, as is often the case, the enthalpy represents the total energy of a fluid. For high-speed
flows, such as those encountered in jet engines, the potential energy of the fluid is still negligible,
but the kinetic energy is not. In such cases, it is convenient
to combine the enthalpy and the kinetic energy of the fluid into a single term called stagnation (or
total) enthalpy ℎ0 , defined per unit mass as
ℎ0 = ℎ +
𝑣2
2
When the potential energy of the fluid is negligible, the stagnation enthalpy
represents the total energy of a flowing fluid stream per unit mass. Thus it
simplifies the thermodynamic analysis of high-speed flows.
During a stagnation process, the kinetic energy of a fluid is converted to
enthalpy (internal energy + flow energy), which results in an increase in the
fluid temperature and pressure. The properties of a fluid at the stagnation
state are called stagnation properties (stagnation temperature, stagnation pressure, stagnation
density, etc.). The stagnation state and the stagnation
properties are indicated by the subscript 0
29

30. Converging–Diverging Nozzles
When we think of nozzles, we ordinarily think of flow passages whose
cross-sectional area decreases in the flow direction. However, the highest
velocity to which a fluid can be accelerated in a converging nozzle is limited to the sonic velocity (𝑀𝑎 =
1), which occurs at the exit plane (throat) of the nozzle. Accelerating a fluid to supersonic velocities
(𝑀𝑎 > 1) can be accomplished only by attaching a diverging flow section to the subsonic nozzle at the
throat. The resulting combined flow section is a converging–diverging nozzle, which is standard
equipment in supersonic aircraft and rocket propulsion (Fig. 12–20).
30

31. Fluid flow around submerged objects (external flow)
Fluid flow over solid bodies frequently occurs in practice, and it is responsible for numerous physical
phenomena such as the drag force acting on automobiles, power lines, trees, and underwater pipelines;
the lift developed by bird or airplane wings; upward draft of rain, snow, hail, and dust particles in high
winds; the transportation of red blood cells by blood flow; the entrainment and disbursement of liquid
droplets by sprays; the vibration and noise generated by bodies moving in a fluid; and the power
generated by wind turbines (Fig. 11–1). Therefore, developing a good understanding of external flow is
important in the design of many engineering systems such as aircraft, automobiles, buildings, ships,
submarines, and all kinds of turbines. Late-model cars, for example, have been designed with particular
emphasis on aerodynamics. This has resulted in significant reductions in fuel consumption and noise, and
considerable improvement in handling. Sometimes a fluid moves over a stationary body (such as the
wind blowing over a building), and other times a body moves through a quiescent fluid (such as a car
moving through air). These two seemingly different processes are equivalent to each other; what matters
is the relative motion between the fluid and the body. Such motions are conveniently analyzed by fixing
the coordinate system on the body and are referred to as flow over bodies or external flow. The
aerodynamic aspects of different airplane wing designs, for example, are studied conveniently in a lab by
placing the wings in a wind tunnel and blowing air over them by large fans.
31

32. 32

33. Also, a flow can be classified as being steady or unsteady, depending on the reference
frame selected. Flow around an airplane, for example, is always unsteady with respect to
the ground, but it is steady with respect to a frame of reference moving with the airplane at
cruise conditions. The flow fields and geometries for most external flow problems are too
complicated to be solved analytically, and thus we have to rely on correlations based on
experimental data. Such testing is done in wind tunnels. H. F. Phillips (1845–1912) built the
first wind tunnel in 1894 and measured lift and drag. The velocity of the fluid approaching a
body is called the free-stream velocity and is denoted by 𝑉. It is also denoted by 𝑢∞or 𝑈∞
when the flow is aligned with the 𝑥-axis since 𝑢 is used to denote the x-component of
velocity. The fluid velocity ranges from zero at the body surface (the no slip condition) to
the free-stream value away from the body surface, and the subscript “infinity” serves as a
reminder that this is the value at a distance where the presence of the body is not felt. The
free-stream velocity may vary with location and time (e.g., the wind blowing past a
building). But in the design and analysis, the free-stream velocity is usually assumed to be
uniform and steady for convenience. The shape of a body has a profound influence on the
flow over the body and the velocity field.
33

34. The flow over a body is said to be two-dimensional when the body is very long and of
constant cross section and the flow is normal to the body. The wind blowing over a long
pipe perpendicular to its axis is an example of two-dimensional flow. A bullet piercing
through air is an example of axisymmetric flow. The velocity in this case varies with the
axial distance x and the radial distance r. Flow over a body that cannot be modeled as two-
dimensional or axisymmetric, such as flow over a car, is three-dimensional (Fig. 11–2).
Flow over bodies can also be classified as incompressible flows (e.g., flows over
automobiles, submarines, and buildings) and compressible flows (e.g., flows over high-
speed aircraft, rockets, and missiles). Bodies subjected to fluid flow are classified as being
streamlined or bluff, depending on their overall shape. A body is said to be streamlined if a
conscious effort is made to align its shape with the anticipated streamlines in the flow.
Streamlined bodies such as race cars and airplanes appear to be contoured and sleek.
Otherwise, a body (such as a building) tends to block the flow and is said to be bluff or
blunt. Usually it is much easier to force a streamlined body through a fluid, and thus
streamlining has been of great importance in the design of vehicles and airplanes (Fig. 11–
3)
34

35. DRAG AND LIFT
A fluid may exert forces and moments on a body in and about various directions. The force a
flowing fluid exerts on a body in the flow direction is called drag. The drag force can be
measured directly by simply attaching the body subjected to fluid flow to a calibrated spring
and measuring the displacement in the flow direction (just like measuring weight with a
spring scale). Drag is usually an undesirable effect, like friction, and we do our best to
minimize it. Reduction of drag is closely associated with the reduction of fuel consumption in
automobiles, submarines, and aircraft; improved safety and durability of structures subjected
to high winds; and reduction of noise and vibration.
A stationary fluid exerts only normal pressure forces on the surface of a body immersed in it.
A moving fluid, however, also exerts tangential shear forces on the surface because of the no-
slip condition caused by viscous effects. Both of these forces, in general, have components in
the direction of flow, and thus the drag force is due to the combined effects of pressure and
wall shear forces in the flow direction. The components of the pressure and wall shear forces
in the direction normal to the flow tend to move the body in that direction, and their sum is
called lift.
35

36. The fluid forces may also generate moments and cause the body to rotate. The
moment about the flow direction is called the rolling moment, the moment about the
lift direction is called the yawing moment, and the moment about the side force
direction is called the pitching moment. For bodies that possess symmetry about the
lift–drag plane such as cars, airplanes, and ships, the time-averaged side force, yawing
moment, and rolling moment are zero when the wind and wave forces are aligned with
the body. What remain for such bodies are the drag and lift forces and the pitching
moment. For axisymmetric bodies aligned with the flow, such as a bullet, the only time-
averaged force exerted by the fluid on the body is the drag force.
36

37. Consider a body held stationary in a stream of real fluid moving at a uniform velocity 𝑉. The force
acting at any point on the small element 𝑑𝐴 of the surface of the body can be considered to have
two components 𝜏𝑑𝐴 and 𝑝𝑑𝐴 acting along the directions tangential and normal to the surface
respectively as shown in figure. The tangential components are ‘shear forces’ and the normal
components are ‘pressure forces’. The drag on the body is therefore given by the summation of the
components of these forces acting over the entire surface of the body in the direction of the fluid
motion. The sum of the components of the shear forces in the direction of flow of fluid is called the
friction drag 𝐹 𝐷 𝑓
which may be expressed as:
Friction drag : 𝐹 𝐷 𝑓
= 𝐴
𝜏𝑑𝐴 cos 𝜃
Similarly the sum of the components of the pressure forces in the direction of the fluid motion is
called the pressure drag 𝐹 𝐷 𝑝
which maybe expressed as:
Pressure drag 𝐹 𝐷 𝑝
= 𝐴
𝑝𝑑𝐴 sin 𝜃
The total drag 𝐹 𝐷 acting on the body is therefore equal to the sum of the friction drag and the
pressure drag. Thus, 𝐹 𝐷 = 𝐹 𝐷 𝑓
+ 𝐹 𝐷 𝑝
=
𝐴
𝜏𝑑𝐴 cos 𝜃 +
𝐴
𝑝𝑑𝐴 sin 𝜃
37

38. 38

39. The relative magnitude of the two components of
the total drag friction drag and pressure drag
depends on the shape and the position of the
immersed body. Thus if a thin plate is held
immersed in a fluid parallel to the direction of
flow as shown in figure 18.3 (a), the pressure drag
( 𝐴
𝑝𝑑𝐴 sin 𝜃) is practically equal to zero. As such
in this case the total drag is equal to the friction
drag. On the other hand if the same plate is held
perpendicular to the flow as shown in figure
18.3(b), the friction drag ( 𝐴
𝜏𝑑𝐴 cos 𝜃) is
practically equal to zero and the total drag is due
to the pressure difference between the upstream
and downstream sides of the plate. In between
these two extreme cases there are several body
shapes for which the contribution of the two
components to the total drag varies considerably
depending on the shape and position of the
immersed body, and the flow and fluid
characteristics.
39

40. The lift on the body is given by the summation of the components of the shear and the pressure
forces acting over the entire surface of the body in the direction perpendicular to the direction of the
fluid motion. Thus following expression is obtained for the total lift 𝐹𝐿 acting on the body shown in
figure 18.2
𝐹𝐿 =
𝐴
𝜏𝑑𝐴 sin 𝜃 +
𝐴
𝑝𝑑𝐴 cos 𝜃
For a body moving through a fluid of mass density 𝜌, at a uniform velocity 𝑉 the mathematical
expressions for the calculation of the drag and the lift may also be written as follows:
𝐹 𝐷 = 𝐶 𝐷 𝐴
𝜌𝑉2
2
𝐹𝐿 = 𝐶𝐿 𝐴
𝜌𝑉2
2
In the above expressions 𝐶 𝐷 and 𝐶𝐿 are known as drag and lift coefficients respectively both of which
are dimensionless. The area 𝐴 is a characteristic area which is usually taken as either the largest
projected area of the immersed body on a plane perpendicular to the direction of flow of fluid. The
term (𝜌𝑉2/2) is the dynamic pressure of the flowing fluid.
40

41. Reducing Drag by Streamlining
Streamlining reduces air resistance by providing a smooth surface over which air flows easily and uniformly. Without
streamlining, eddies formed on the trailing edges of objects create turbulent, low-pressure areas and increase air resistance,
also known as drag
Streamlining allows objects to move more efficiently through the air by parting the air ahead of them and allowing it to
recombine as the objects pass, according to Science Learning Hub. The typical teardrop shape is an example of streamlining in
which the air is allowed to slip back together smoothly in the wake of the object. The teardrop shape keeps the flow of air
close to the surface at all times, resulting in a smooth recombination of the air displaced. Other shapes, such as circles, force
the oncoming air upward as it moves towards the trailing edge. This not only creates eddies, but also disrupts the flow of air
above the surface, further increasing aerodynamic drag.
Streamlining is very apparent within the sport of cycling and in the design of airplanes and modern automobiles. The
streamlined shapes of planes and vehicles take advantage of the lowered air resistance to reduce fuel consumption. In the
same way, a cyclist with a teardrop-shaped helmet crouches down to allow the air to slip over him smoothly and recombine,
increasing his speed. 41

42. An airfoil (in American English) or aerofoil (in British English) is the shape of a wing, blade (of a
propeller, rotor, or turbine), or sail (as seen in cross-section).
An airfoil-shaped body moved through a fluid produces an aerodynamic force. The component of
this force perpendicular to the direction of motion is called lift. The component parallel to the
direction of motion is called drag. Subsonic flight airfoils have a characteristic shape with a rounded
leading edge, followed by a sharp trailing edge, often with a symmetric curvature of upper and
lower surfaces. Foils of similar function designed with water as the working fluid are called
hydrofoils.
The lift on an airfoil is primarily the result of its angle of attack and shape. When oriented at a
suitable angle, the airfoil deflects the oncoming air (for fixed-wing aircraft, a downward force),
resulting in a force on the airfoil in the direction opposite to the deflection. This force is known as
aerodynamic force and can be resolved into two components: lift and drag. Most foil shapes require
a positive angle of attack to generate lift, but cambered airfoils can generate lift at zero angle of
attack. This "turning" of the air in the vicinity of the airfoil creates curved streamlines, resulting in
lower pressure on one side and higher pressure on the other. This pressure difference is
accompanied by a velocity difference, via Bernoulli's principle, so the resulting flow field about the
airfoil has a higher average velocity on the upper surface than on the lower surface. The lift force
can be related directly to the average top/bottom velocity difference without computing the
pressure by using the concept of circulation and the Kutta-Joukowski theorem.
Airfoil
42

43. 43

44. 44
Theory of lift (Two-dimensional thin airfoils)
Consider a 2-D flow past a thin airfoil and assume that the flow does not separate and can be modelled as a potential
flow (i.e. airfoil is smooth). We can use Bernoulli’s theorem to calculate the pressure — recall that there is no drag
force acting on a solid body placed in a potential flow.
For a flat airfoil, the force in the upward vertical direction will be the difference between pressure forces on the
bottom and on the top of the airfoil. This force per unit length is
𝐹 = 𝑃𝐵 − 𝑃 𝑇 𝑑𝑥
Using Bernoulli’s theorem,
𝑃 𝐵
𝜌
+
1
2
𝑢 𝐵
2
=
𝑃 𝑇
𝜌
+
1
2
𝑢 𝑇
2
𝐹 =
𝜌
2
𝑢 𝑇
2
− 𝑢 𝐵
2
𝑑𝑥 =
𝜌
2
𝑢 𝑇 − 𝑢 𝐵 𝑢 𝑇 + 𝑢 𝐵 𝑑𝑥
For a thin airfoil, both 𝑢 𝑇 and 𝑢 𝐵 and will be close to U (the free stream velocity), so that

45. 45
𝑢 𝑇 + 𝑢 𝐵 ≃ 2𝑈 ⟹ 𝐹 ≃ 𝜌𝑈 𝑢 𝑇 − 𝑢 𝐵 𝑑𝑥 = −ρ𝑈
𝐶
𝑢. 𝑑𝑙 where 𝐶 is the curve around the airfoil.
Thus, the force acting on the airfoil, 𝐹 = −𝜌𝑈Γ where Γ = 𝐶
𝑢. 𝑑𝑙 , is proportional to the circulation around the
wing (Γ is capital Greek letter gamma )
This is called the Kutta-Joukowski theorem

46. 46
The End