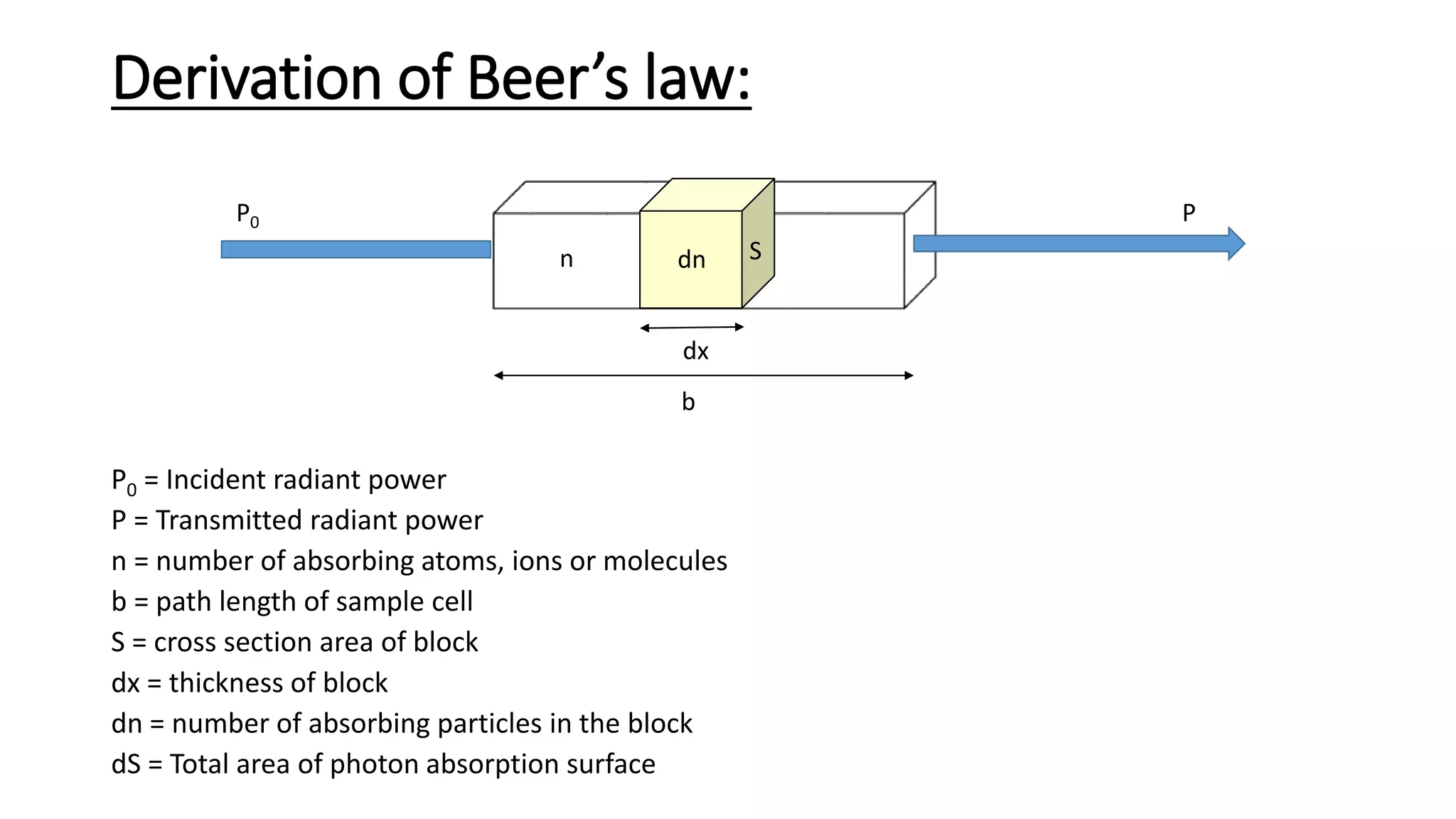
This document discusses Beer's law, which states that absorbance of a solution is directly proportional to the concentration of the absorbing material in the solution. It defines Beer's law, derives the mathematical equation, and lists some limitations and sources of deviation from the law, including high concentrations, dissociation/association reactions, use of polychromatic radiation, stray light, and mismatched sample cells. The derivation shows how the Beer's law equation is obtained based on probability of photon absorption in thin sections of the sample.

1. Beer’s Law
By- Krishan Kumar Verma, Assistant Professor
Ram-Eesh Institute of Vocational & Technical Education

2. Learning Outcomes:
The learners will be able to-
• Define Beer’s law
• Derive Beer’s law

3. Introduction
• UV-Visible spectroscopy is a type of absorption spectroscopy.
• Absorption spectroscopy involves measurement of absorbance or
transmittance of sample contained in a transparent cell with path length
of b cm.
• Absorbance is inversely proportional to transmittance.
• Absorption of light is mainly governed by Beer’s law

4. A = log
1
T
= − log T = log (Po/P) = ε b c
A = Absorbance
T = Transmittance
P0 = Incident radiant power
P = Transmitted radiant power
ε = Molar absorptivity (previously molar extinction coefficient)
b = Path length of sample cell(cm)
C = Concentration of sample (mol L-1)

5. Derivation of Beer’s law:
P0 = Incident radiant power
P = Transmitted radiant power
n = number of absorbing atoms, ions or molecules
b = path length of sample cell
S = cross section area of block
dx = thickness of block
dn = number of absorbing particles in the block
dS = Total area of photon absorption surface
b
P0 P
n
dx
Sdn

6. • The ratio of photon capture are to the total area =
dS
S
This represents the probability for capture of photon with in the section.
• The power of beam entering the section, Px, is proportional to the
number of photons per unit area and dPx represents the power
absorbed with in the section.
Therefore, the fraction absorbed = −
dPx
Px
(- sign indicates decrease in power after absorption)
• This ratio is equal to the average probability of photon capture;
−
𝑑𝑃𝑥
𝑃𝑥
=
𝑑𝑆
𝑆
1

7. dS α dn
dS = a dn
Replacing the dS to equation 1,
−
𝑑𝑃𝑥
𝑃𝑥
=
𝑎 𝑑𝑛
𝑆
− ln
𝑃
𝑃0
=
𝑎 𝑛
𝑆
log
𝑃0
𝑃
=
𝑎 𝑛
2.303 𝑆
𝑃0
𝑃
𝑑𝑃𝑥
𝑃𝑥
=
0
𝑛
𝑎 𝑑𝑛
𝑆

8. log
𝑃0
𝑃
=
𝑎 𝑛
2.303 𝑆
log
𝑃0
𝑃
=
𝑎 𝑛 𝑏
2.303 𝑉
𝑠𝑖𝑛𝑐𝑒, 𝑆 =
𝑉 𝑐𝑚3
𝑏 𝑐𝑚
Now
𝑛
𝑉
may be converted to concentration (mol L-1)
Number of mol =
n particles
6.022 x 1023 particles per mol
C = 𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑚𝑜𝑙𝑒𝑠
𝐿𝑖𝑡𝑟𝑒𝑠
=
n particles
6.022 x 1023 particles per mol
1000 cm3 L−1
V cm3
2

9. After replacing
𝑛
𝑉
concentration (mol/L)
log
𝑃0
𝑃
=
6.022 x 1023
𝑎 𝑏 𝑐
2.303 x 1000
Finally, after combining all the constants;
log
𝑃0
𝑃
= ε b c = A (Beer’s law equation)
ε = molar absorptivity

10. For multicomponent systems:
• When more than one absorbing species are present.
• The absorbing species must not interact with each other.
Total absorbance (A Total) = A1 + A2 + A3 + …………….An
= ε1bc + ε2bc + ε3bc + ……………. εnbc

11. Limitations & Deviations-
Beer’s Law
By- Krishan Kumar Verma, Assistant Professor
Ram-Eesh Institute of Vocational & Technical Education

12. Limitations to Beer’s law:
According to Beer’s law, A α C (linear relation)
Concentration
Absorbance

13. Real limitations to Beer’s law:
• Beer’s law is applicable only at very low concentration (≤ 0.01M).
• At high concentrations, average distance between molecules or ions
decreases.
• The solute-solute, solute-solvent, hydrogen bonding and electrostatic
interactions may increase that can alter absorptivity and hence may
cause deviations from linear relation.
• Absorptivity also depends on refractive index of the medium, that can
be altered by varying concentration.
Correction to be done: use
ε 𝑛
𝑛2
+2 2 instead of ε

14. Apparent chemical deviations:
• Involves dissociation or association of analyte.
• Reaction of analyte with solvent to produce a product with different
absorption spectrum than analyte.
e.g. In acid-base indicators
HIn H+ + In-
(color I) (color II)
For unbuffered solution,
At 430 nm, absorption is due to In-
At 570 nm, absorption is due to HIn
Indicator concentration
Absorbance
-ve deviation
(at 570 nm)
+ve deviation
(at 430 nm)

15. Instrumental deviations:
1. Due to polychromatic radiation:
Consider a beam with two wavelength, λ’ and λ’’
For λ’
A’ = ε’ b c
𝑃0
′
𝑃′ = 10 -ε’bc
P’ = P0’10 ε’bc
For λ’’
P’’ = P0’’10 ε’’bc
The overall combined absorbance can be written as-
Am = log (
𝑃0
′
+𝑃0
′′
𝑃′
+𝑃′′ )

16. Am = log
(𝑃0
′+𝑃0
′′)
(𝑃0
′10
_
εbc + 𝑃 0
′′
10
_
ε′′bc)
When molar absorptivity's are same at two wavelengths, Beer’s law is
followed.
Am = ε′bc = ε′′bc
But when ε′ and ε′’ are not equal, relationship becomes non linear.
Concentration
Absorbance
ε′ = ε′′ = 1000
ε′ = 1500, ε′′ = 500
ε′ = 1750, ε′′ = 250

17. 2. Due to stray radiation:
• Radiation coming from monochromator is usualy contaminated with
small amounts of scattered or stray radiation.
• Stray light is the radiation from instrument that is outside the nominal
wavelength band chosen for determination.
• Stray light may be observed due to scattering, reflections of gratings
surfaces, lens or mirrors.
• Stray radiation wavelength often differs from principal radiation and
may not have passed through sample.
• Necessary correction:
A’ = log (
𝑃0+𝑃𝑆
𝑃+𝑃𝑆
)
PS = power of stray radiation

18. 3. Due to mismatched cell:
• Mismatch between analyte and blank cell.
• Unequal path lengths and optical properties
• Can be corrected by linear regression, use of single beam instrument
or addition of intercept in Beer’s law equation.
A = εbc + k
Concentration
Absorbance
0 %
0.2 %
1 %
5 %
𝑃 𝑆
𝑃0
x100 %

19. THANK YOU