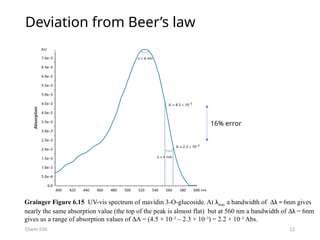
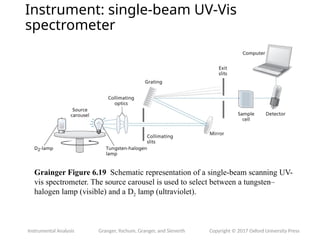
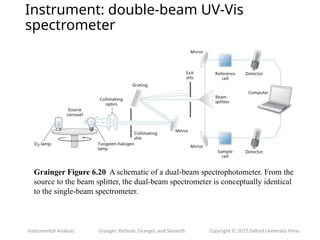
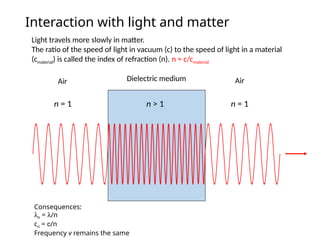
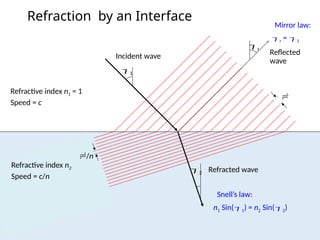
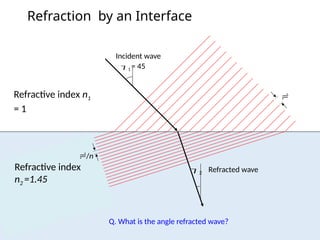
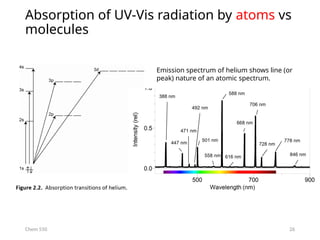
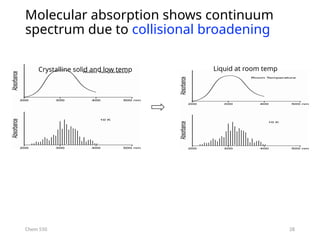
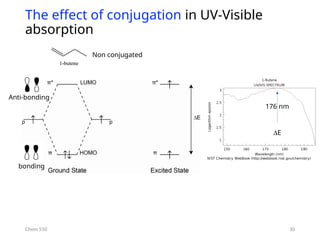
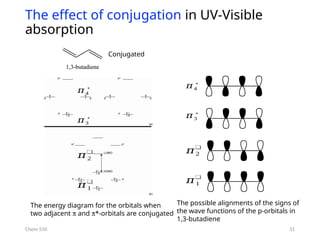
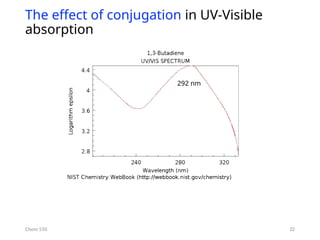
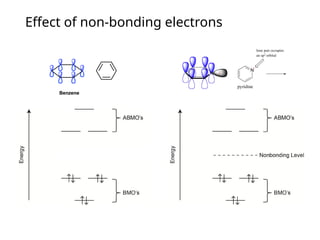
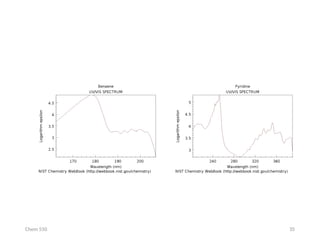
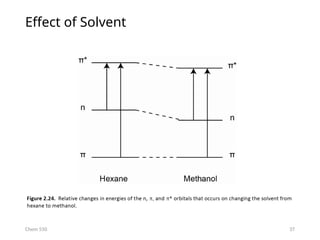
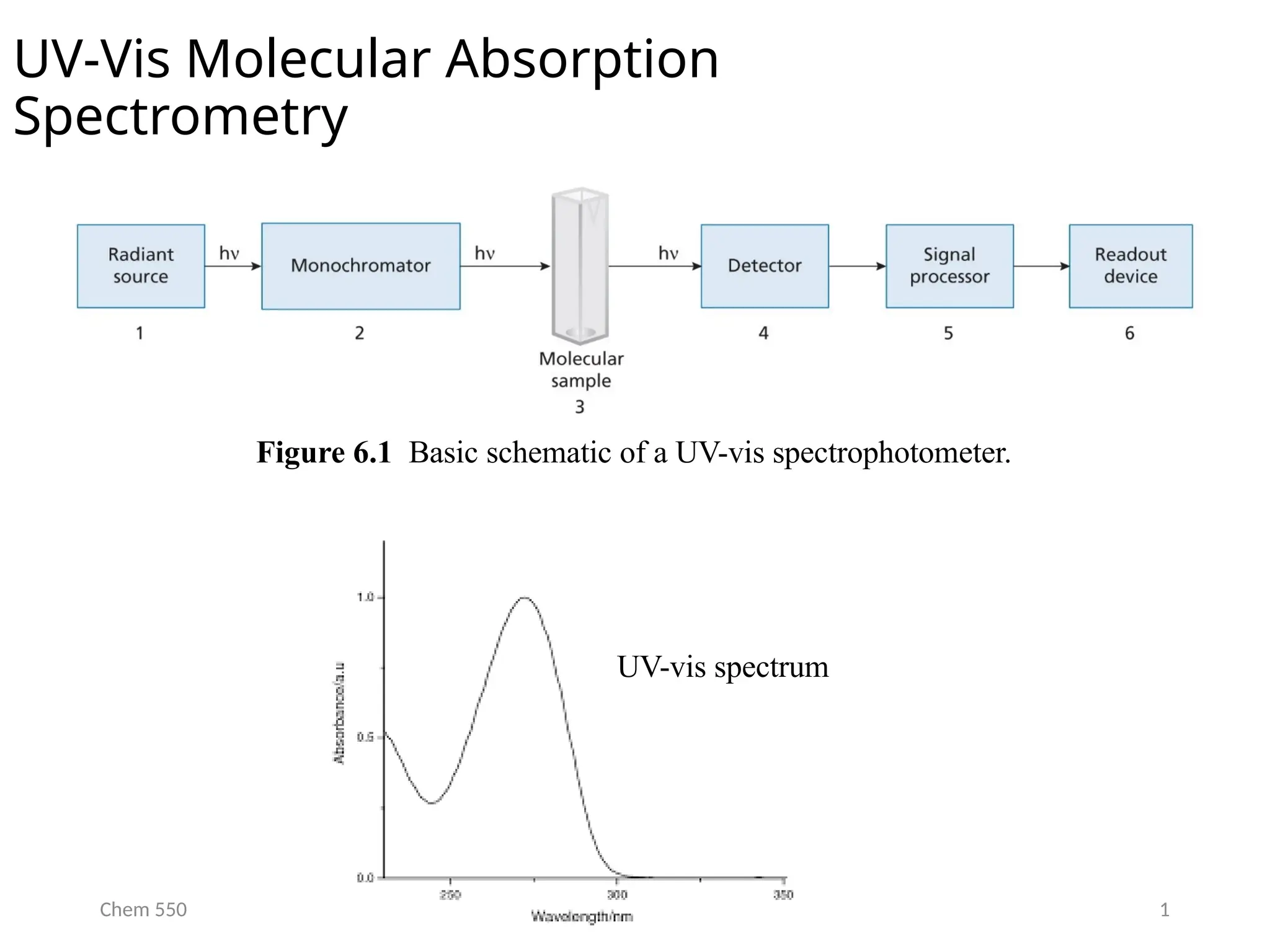
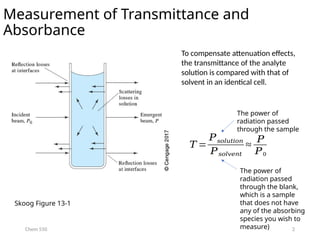
The document provides an overview of UV-Vis spectrophotometry principles, including the measurement of absorbance and transmittance, the application of Beer’s Law, and factors affecting absorbance like concentration and pathlength. It discusses deviations from Beer’s Law due to high concentrations, polychromatic radiation, and instrumental factors, while explaining the ideal conditions for accurate measurements. Additionally, it covers the interaction of electromagnetic radiation with matter, atomic versus molecular absorption, and the effects of conjugation on UV-visible absorption spectra.

1. 1
Chem 550
Figure 6.1 Basic schematic of a UV-vis spectrophotometer.
UV-Vis Molecular Absorption
Spectrometry
UV-vis spectrum

2. 2
Chem 550
Measurement of Transmittance and
Absorbance
Skoog Figure 13-1
To compensate attenuation effects,
the transmittance of the analyte
solution is compared with that of
solvent in an identical cell.
𝑇 =
𝑃𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛
𝑃𝑠𝑜𝑙𝑣𝑒𝑛𝑡
≈
𝑃
𝑃0
The power of
radiation passed
through the sample
The power of
radiation passed
through the blank,
which is a sample
that does not have
any of the absorbing
species you wish to
measure)

3. Measurement of Transmittance and
Absorbance
𝐴=− 𝑙𝑜𝑔𝑇 =−𝑙𝑜𝑔
𝑃
𝑃 0
=𝜀𝑏𝑐
For non-interacting multiple component systems
Beer’s law
Chem 550 3
What is the factors that influence the
absorbance of the sample? Is each factor
directly or inversely proportional to the
absorbance?
• Concentration
• Pathlength
• Molar absorptivity or molar extinction
coefficient

4. 4
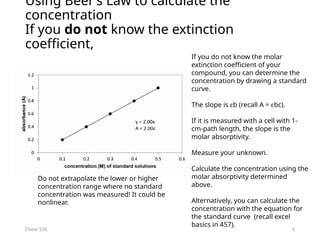
Using Beer’s Law to calculate the
concentration
If you know the extinction coefficient,
Chem 550
Figure 6.12 UV-vis spectrum of 1-10-phenanthroline-5,6-dione platinum(IV)
chloride [Pt(dione)Cl4] in dry acetonitrile.
Absorbance
A = 0.145
**290.5 nm seem to be a typo. It should be ~315 nm.
What is the concentration of the
compound? The path length of the cell
is 1 cm.

5. 5
Chem 550
Using Beer’s Law to calculate the
concentration
If you do not know the extinction
coefficient,
If you do not know the molar
extinction coefficient of your
compound, you can determine the
concentration by drawing a standard
curve.
The slope is eb (recall A = ebc).
If it is measured with a cell with 1-
cm-path length, the slope is the
molar absorptivity.
Measure your unknown.
Calculate the concentration using the
molar absorptivity determined
above.
Alternatively, you can calculate the
concentration with the equation for
the standard curve (recall excel
basics in 457).
Do not extrapolate the lower or higher
concentration range where no standard
concentration was measured! It could be
nonlinear.

6. 6
Chem 550
Figure 6.13 A representation of the linearity of Beer’s law as a
function of concentration. Beer’s law is generally linear below
one absorbance. Above one absorbance, the slope of the Abs.
vs. Conc. line usually bends towards zero.
1. Internal Screening from too high absorbance > 1
The concentration is so high that
some of the absorbing species lie
within the “shadow” of other
absorbing species and are hidden
from radiant source.
Figure 6.14 A representation of internal
screening.
Solution: Keep the absorbance below 1.
Deviation from Beer’s law

7. 7
Deviation from Beer’s law
Chem 550
• If molar absorptivity, Beer’s law deviates at high
concentration. interaction between solutes change the
• Beer’s law describes the absorption behavior of media at
low analyte concentration (<10 mM).
• Refractive index change of a solution. The absorptivity
depends on the index of refraction (n).
e’ = en/(n2
+2)2
2. Concentration limit

8. 9
Chem 550
3. Instrumental Deviations due to Polychromatic Radiation
• Beer’s law strictly applies only when measurements are made with
monochromatic source radiation.
o It is not possible to get purely monochromatic radiation
using a dispersing element with a slit.
o The sample has a slightly different molar absorptivity for
each wavelength of radiation.
• When the molar absorptivities are not the same for composing
wavelengths, the total absorbance added over all the different
wavelengths is no longer linear with concentration.
𝐴𝑡𝑜𝑡𝑎𝑙 =𝑙𝑜𝑔
( 𝑃 ′ 0 + 𝑃0
′ ′
)
¿ ¿
𝜀𝜆′ ≠ 𝜀𝜆′′
,
When
Deviation from Beer’s law

9. 10
Deviation from Beer’s law
Chem 550
3. Instrumental Deviations due to Polychromatic
Radiation
Skoog Fig 13-4
Deviations from Beer’s law with
Polychromatic radiation.
Absorber has the indicated molar
absorptivities at the two
wavelengths l’ and l .
”

10. 11
Deviation from Beer’s law
Chem 550
3. Instrumental Deviations due to Polychromatic
Radiation
• Select the band of wavelengths selected for
spectrophotometeric measurements such that the molar
absorptivities are essentially constant.
• Select a wavelength band near the wavelength of maximum
absorption.
• Monochromator or filter ∆eff < 1/10 of the absorption band
of full width at half maximum
Fig 13-4 Skoog Fig 13-5
Polychromatic band A
causes less band Beer’s law
deviation because of less
ℇ within band A.
∆

11. 12
Deviation from Beer’s law
Chem 550
Grainger Figure 6.15 UV-vis spectrum of mavidin 3-O-glucoside. At λmax a bandwidth of Dλ = 6nm gives
nearly the same absorption value (the top of the peak is almost flat) but at 560 nm a bandwidth of Dλ = 6nm
gives us a range of absorption values of DA = (4.5 × 10–3
– 2.3 × 10–3
) = 2.2 × 10–3
Abs.
16% error

12. Instrumental Analysis Granger, Yochum, Granger, and Sienerth Copyright © 2017 Oxford University Press
Grainger Figure 6.19 Schematic representation of a single-beam scanning UV-
vis spectrometer. The source carousel is used to select between a tungsten–
halogen lamp (visible) and a D2 lamp (ultraviolet).
Instrument: single-beam UV-Vis
spectrometer

13. Instrumental Analysis Granger, Yochum, Granger, and Sienerth Copyright © 2017 Oxford University Press
Grainger Figure 6.20 A schematic of a dual-beam spectrophotometer. From the
source to the beam splitter, the dual-beam spectrometer is conceptually identical
to the single-beam spectrometer.
Instrument: double-beam UV-Vis
spectrometer

14. 16
Instrument Component: Source
Chem 550
To measure absorption spectrum, the UV-
Vis spectrometer requires continuum
source whose radiant power does not
sharply change over a considerable range
of wavelengths.
Deuterium and Hydrogen Lamps:
• UV region (190-400 nm)
• Electrical discharge lamp.
• Formation of excited molecular
deuterium followed by dissociation into
atomic deuterium produces various
wavelengths of UV light.

15. 17
Chem 550
Tungsten Filament Lamps:
• Visible region (350-2500 nm)
• Spectrum follows black-body radiation
• Tungsten filament lamps.
o Operated at 2870K.
• Tungsten-halogen lamps (Quartz-
halogen lamp).
o Operated at 3500K.
o Enhanced lifetime because
sublimated W forms a volatile
product WI2 that allow W to be
redeposited to the filament.
LED: White LED (400-800 nm) or
semimonochromatic
Xenon Arc Lamps: 200-1000 nm.
Instrument Component: Source

16. Instrumental Analysis Granger, Yochum, Granger, and Sienerth Copyright © 2017 Oxford University Press
Figure 6.27 (left) A schematic of an eight-stage PMT and (right) a photograph of a
PMT. The incident photon dislodges an electron from the scintillator, which initiates
a cascade of ejected electrons as they proceed toward the collector.
Instrument Component: Detector
Photomultiplier tube

17. 19
Chem 550
Figure 6.29 An MOS semiconductor used in a
CCD detector.
Instrument Component: Detector
Charge Coupled Device (CCD)
CCD is used in an array format.
No exit slit in monochromator.

18. 20
Chem 550

19. Supplementary
discussion of
electromagnetic
radiation

20. Interaction with light and matter
n = 1 n > 1 n = 1
Light travels more slowly in matter.
The ratio of the speed of light in vacuum (c) to the speed of light in a material
(cmaterial) is called the index of refraction (n). n = c/cmaterial
Air Dielectric medium Air
Consequences:
ln = l/n
cn = c/n
Frequency v remains the same

21. Reflected
wave
r
Refraction by an Interface
Refractive index n1 = 1
Speed = c
Refractive index n2
Speed = c/n
Incident wave
1
Refracted wave
2
Snell’s law:

/n
Mirror law:
r = 1
n1 Sin(1) = n2 Sin(2)

22. Refraction by an Interface
Refractive index n1
= 1
Refractive index
n2 =1.45
Incident wave
1 = 45
Refracted wave
2

/n
Q. What is the angle refracted wave?

23. UV-Visible
Spectroscopy

24. 26
Absorption of UV-Vis radiation by atoms vs
molecules
Chem 550
Emission spectrum of helium shows line (or
peak) nature of an atomic spectrum.

25. 27
Absorption of UV-Vis radiation by atoms vs
molecules
Chem 550
Atomic absorption
Molecular absorption
Molecular energy levels

26. 28
Chem 550
Molecular absorption shows continuum
spectrum due to collisional broadening
Liquid at room temp
Crystalline solid and low temp

27. 29
Possible electronic transitions in organic
compounds
Chem 550
The σ to σ* transition requires an absorption of a photon with a
wavelength which does not fall in the UV-vis range (~ < 130 nm). Thus,
only π to π* and n to π* transitions occur in the UV-vis region are
observed (>160 nm).

28. 30
The effect of conjugation in UV-Visible
absorption
Chem 550
Anti-bonding
bonding
DE
Non conjugated
176 nm

29. 31
Chem 550
Conjugated
The effect of conjugation in UV-Visible
absorption
The energy diagram for the orbitals when
two adjacent p and p*-orbitals are conjugated
𝜋4
∗
𝜋3
∗
𝜋2
❑
𝜋1
❑
𝜋4
∗
𝜋3
∗
𝜋2
❑
𝜋1
❑
The possible alignments of the signs of
the wave functions of the p-orbitals in
1,3-butadiene

30. 32
The effect of conjugation in UV-Visible
absorption
Chem 550
292 nm

31. 33
Structure and color in conjugated systems
Chem 550
Figure 6.5 UV-vis spectra of anthracene and tetracene.
The energy level in a ”Particle in a box”
h = Planck’s constant
n = positive whole number
representing the quantum state
m = mass
L = length of the “box”
L increases as the degree of
conjugation increases. In other
words, the energy gap between p
and p* decreases.

32. Effect of non-bonding electrons

33. 35
Chem 550

34. 36
Effect of Solvent
Chem 550

35. 37
Effect of Solvent
Chem 550