Download to read offline
Uploaded bysushma chinta
Bars with variable cross sections subjected to axial loads
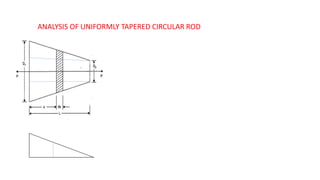
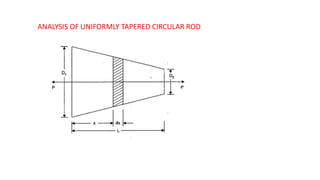
The document discusses the analysis of uniformly tapered circular rods and rectangular bars subjected to axial loads. It provides equations to calculate the stress, strain, and extension of tapered bars based on the load, dimensions, Young's modulus, and taper rate. Several example problems are included to demonstrate calculating extension given dimensions and load, or determining Young's modulus given the other values. The document also discusses calculating the elongation of a bar due to its own weight by integrating the strain over the length of the bar.
More Related Content
Similar to Bars with variable cross sections subjected to axial loads
More from sushma chinta
Bars with variable cross sections subjected to axial loads
- 2. ANALYSIS OF UNIFORMLYTAPERED CIRCULAR ROD P = Axial tensile load on the bar L = Total length of the bar E = Young's modulus. D1= Diameter of rod at big end D2= Diameter of rod at small end
- 3. Consider a smallelement of length dx of the bar at a distance x from the left end. Let the diameter of the bar be ‘D’ at a distance x from the left end. Area of cross-section of the bar at a distance x from the left end A = 𝜋 4 𝐷2
- 4. ANALYSIS OF UNIFORMLYTAPERED CIRCULAR ROD
- 6. ANALYSIS OF UNIFORMLYTAPERED CIRCULAR ROD
- 8. Now the stressat a distance x from the left end is given by 𝜎𝑥 = 𝐿𝑜𝑎𝑑 𝐴 The strain 𝜀 in the small element of length dx is obtained by using equation = 𝜎 𝑥 𝐸 = Extension of the small elemental length dx: dδ = Strain. dx = 𝜀. dx Area of cross-section of the bar at a distance x from the left end A = 𝜋 4 𝐷2 =
- 9.
- 11. ANALYSIS OF UNIFORMLYTAPERED CIRCULAR ROD
- 12. Q1. A rod,which tapers uniformly from 40 mm diameter to 20 mm diameter in a length of 400 mm is subjected to an axial load of 5000 N. If E is 2.1 x 105 N/mm2, find the extension of the rod. Larger diameter, D1= 40mm Smaller diameter, D2 = 20 mm Length of rod, L = 400 mm Axial load, P = 5000 N Young's modulus, E = 2.1 x 105 N/mm2 Let δ= Total extension of the rod 𝛿 = 4𝑃𝐿 𝜋𝐷1 𝐷2 𝐸
- 13. Q2. Find themodulus of elasticity for a rod, which tapers uniformly from 30 mm to 15 mm diameter in a length of 350 mm. The rod is subjected to an axial load of 5.5 kN and extension of the rod is 0.025 mm. Larger diameter,D1= 30mm Smaller diameter,D2= 15mm Length of rod, L=350 mm Axial load, P= 5500 N Extension,δ= 0.025 mm E = 4𝑃𝐿 𝜋𝐷1 𝐷2δ
- 14. ANALYSIS OF UNIFORMLYTAPERING RECTANGULAR BAR p = Axial load on the bar L = Length of bar a = Width at bigger end b = Width at smaller end E = Young's modulus t = Thickness of bar
- 15. Consider a smallelement of length dx of the bar at a distance x from the left end. Let the width of the bar be ‘c’ at a distance x from the left end. Area of cross-section of the bar at a distance x from the left end A =𝑐. 𝑡
- 16. ANALYSIS OF UNIFORMLYTAPERED CIRCULAR ROD
- 17. Now the stressat a distance x from the left end is given by 𝜎𝑥 = 𝐿𝑜𝑎𝑑 𝐴 = 𝑃 𝑎−𝑘𝑥 𝑡 The strain ′𝜀′ in the small element of length dx is obtained by using equation = 𝜎 𝑥 𝐸 = 𝑃 𝑎−𝑘𝑥 𝑡 𝐸 Extension of the small elemental length dx: dδ = Strain. dx = 𝜀. dx= 𝑃. 𝑑𝑥 𝑎−𝑘𝑥 𝑡 𝐸 Area of cross-section of the bar at a distance x from the left end A =C.t = (𝑎 -kx). t
- 18.
- 19. Q3. A rectangularbar made of steel is 2.8 m long and 15 mm thick. The rod is subjected to an axial tensile load of40 kN. The width of the rod varies from 75 mm at one end to 30 mm at the other. Find the extension of the rod if E = 2 X 105 N/mm2. Length, L =2.8 m =2800 mm Thickness, t = 15 mm Axial load, P =40 kN =40,000 N Width at bigger end, a = 75 mm Width at smaller end, b = 30 mm Value of E = 2 X 10 5 N/mm2 Let δ= Extension of the rod. We know δ= 𝑃𝐿 𝐸𝑡 𝑎−𝑏 ln 𝑎 𝑏 δ= 𝑃𝐿 𝐸𝑡 𝑎−𝑏 loge 𝑎 𝑏
- 20. Q4. The extensionin a rectangular steel bar of length 400 mm and thickness 10 mm, is found to be 0.21 mm. The bar tapers uniformly in width from 100 mm to 50 mm. If E for the bar is 2 x 105 N/mm2, determine the axial load on the bar. Extension, δ = 0.21 mm Length, L = 400 mm Thickness, t = 10 mm Width at bigger end, a = 100 mm Width at smaller end, b = 50 mm Value of E = 2 x 105 N/mm2 Let P = axial load. We know δ= 𝑃𝐿 𝐸𝑡 𝑎−𝑏 ln 𝑎 𝑏 δ= 𝑃𝐿 𝐸𝑡 𝑎−𝑏 l𝑜𝑔 𝑒 𝑎 𝑏 ⇒ 𝑃 = 𝛿𝐸𝑡 𝑎−𝑏 𝐿 log 𝑒 𝑎 𝑏
- 21. ELONGATION OF ABAR DUE TO ITS OWN WEIGHT AB is a bar fixed at end A and hanging freely under its own weight. Let L = Length of bar, A =Area of cross-section, E= Young's modulus for the bar material, w= Weight per unit volume of the bar material.
- 22. Consider a smallstrip of thickness dx at a distance x from the lower end. Weight of the bar for a length of x is given by, P= Specific weight x Volume of bar up to length x = Now stress on the element= 𝜎 = 𝑃 𝐴 = Strain in the element= ε = 𝜎 𝐸 =
- 23. Elongation of theelement = Strain x Length of element = ε* dx Total elongation of the bar is obtained by integrating. the above equation between limits zero and L. 𝛿 = 0 𝐿 𝜀 ⅆ𝑥
- 25. Mcq1. The ratioof elongation in a prismatic bar due to its own weight (W) as compared to another similar bar carrying an additional weight (W) will be _________________? A. 1:2 B. 1 : 3 C. 1 : 4 D. 1 : 2.5 E. 1 : 2.25
Editor's Notes
- #23 The above equation shows that stress. due to self weight in a bar is not uniform. It depends on x. The stress increases with the increase of x.