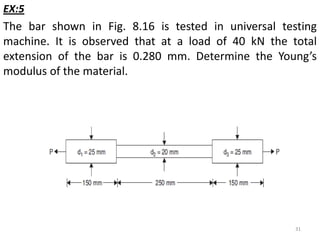
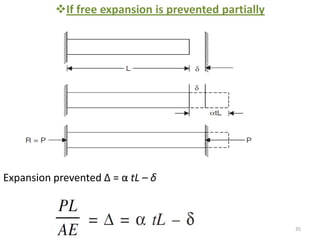
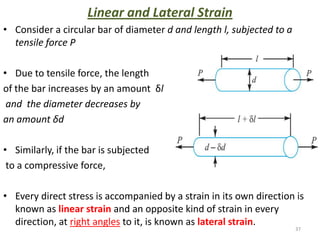
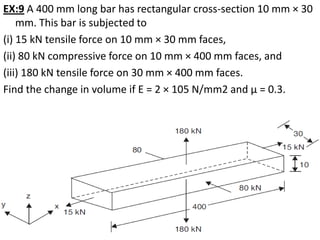
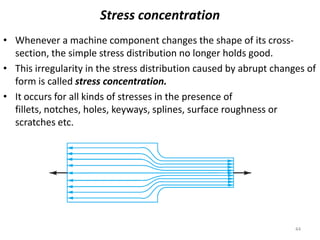
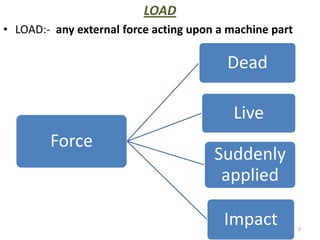
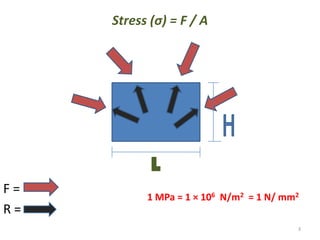
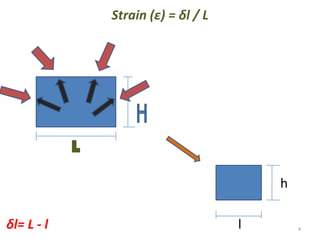
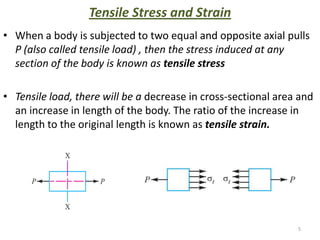
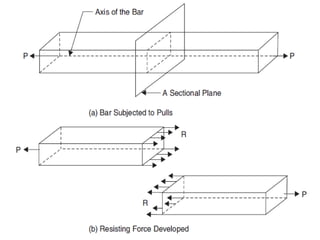
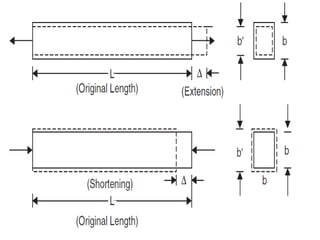
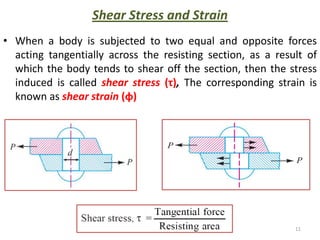
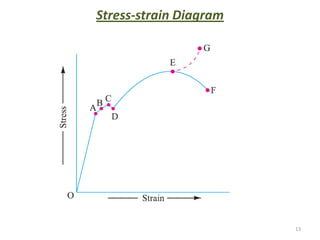
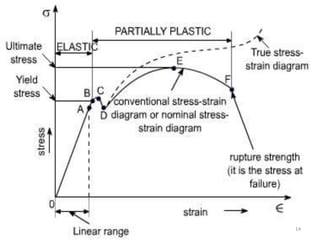
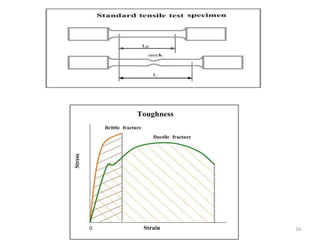
This document contains lecture notes on mechanics of solids from the Department of Mechanical Engineering at Indus Institute of Technology & Engineering. It defines key concepts such as load, stress, strain, tensile stress and strain, compressive stress and strain, Young's modulus, shear stress and strain, shear modulus, stress-strain diagrams, working stress, and factor of safety. It also discusses thermal stresses, linear and lateral strain, Poisson's ratio, volumetric strain, bulk modulus, composite bars, bars with varying cross-sections, and stress concentration. The document provides examples to illustrate how to calculate stresses, strains, moduli, and other mechanical properties for different loading conditions.

1. INDUS INSTITUTE OF
TECHNOLOGY & ENGINEERING
DEPARTMENT OF
MECHANICAL ENGINEERING
Name : Keval Patel
Subject Code :
Subject Name : Mechanics of solid
B.E Mechanical Engineering , 1st Semester
1

2. LOAD
• LOAD:- any external force acting upon a machine part
Dead
Live
Force
Suddenly
applied
Impact 2

3. Stress (σ) = F / A
F=
1 MPa = 1 × 106 N/m2 = 1 N/ mm2
R=
3

4. Strain (ε) = δl / L
h
δl= L - l l 4

5. Tensile Stress and Strain
• When a body is subjected to two equal and opposite axial pulls
P (also called tensile load) , then the stress induced at any
section of the body is known as tensile stress
• Tensile load, there will be a decrease in cross-sectional area and
an increase in length of the body. The ratio of the increase in
length to the original length is known as tensile strain.
5

6. 6

7. Compressive Stress and Strain
• When a body is subjected to two equal and opposite axial
pushes P (also called compressive load) , then the stress induced
at any section of the body is known as compressive stress
• Compressive load, there will be an increase in cross-sectional
area and a decrease in length of the body. The ratio of the
decrease in length to the original length Is known as
compressive strain
7

8. 8

9. Young's Modulus or Modulus of Elasticity
 Hooke's law:- states that when a material is loaded within
elastic limit, the stress is directly proportional to
strain,
σ ∝ ε or σ= E×ε
9

10. Example
1. A circular rod of diameter 16 mm and 500 mm long
is subjected to a tensile force 40 kN. The modulus
of elasticity for steel may be taken as 200 kN/mm2.
Find stress, strain and elongation of the bar due to
applied load.
10

11. Shear Stress and Strain
• When a body is subjected to two equal and opposite forces
acting tangentially across the resisting section, as a result of
which the body tends to shear off the section, then the stress
induced is called shear stress (τ), The corresponding strain is
known as shear strain (φ)
11

12. Shear Modulus or Modulus of Rigidity
• It has been found experimentally that within the elastic
limit, the shear stress is directly proportional to shear strain.
Mathematically τ∝φ or τ=G.φ or τ/φ=G
• where, τ = Shear stress,
• φ = Shear strain,
• G = Constant of proportionality, known as shear modulus or
modulus of rigidity.
It is also denoted by N or C. 12

13. Stress-strain Diagram
13

14. 14

15. 15

16. 16

17. Working Stress
• When designing machine parts, it is desirable to keep the stress
lower than the maximum or ultimate stress at which failure of
the material takes place. This stress is known as the working
stress or design stress.
• It is also known as safe or allowable stress.
working stress = design stress = safe stress = allowable stress
17

18. Factor of Safety
 The ratio of the maximum stress to the working stress.
18

19. 1: A hollow steel tube is to be used to carry an axial compressive load of
160 kN. The yield stress for steel is 250 N/mm2. A factor of safety of
1.75 is to be used in the design. The following three class of tubes of
external diameter 101.6 mm are available.
Class Thickness
• Light 3.65 mm Medium 4.05 mm Heavy 4.85 mm
Which section do you recommend?
2: A specimen of steel 20 mm diameter with a gauge length of 200 mm
is tested to destruction. It has an extension of 0.25 mm under a load
of 80 KN and the load at elastic limit is 102 KN. The maximum load is
130 KN. The total extension at fracture is 56 mm and diameter at
neck is 15 mm. Find
(i) The stress at elastic limit. (ii) Young’s modulus.
(iii) Percentage elongation. (iv) Percentage reduction in area.
(v) Ultimate tensile stress.
19

20. Stresses in Composite Bars
• A composite bar may be defined as a bar made up of two or more
different materials, joined together, in such a manner that the system
extends or contracts as one unit, equally, when subjected to tension
or compression.
1. The extension or contraction of
the bar is being equal
2. The total external load on the bar is
equal to the sum of the loads carried
by different materials.
20

21. • P1 = Load carried by bar 1,
• A1 = Cross-sectional area of bar 1,
• σ1 = Stress produced in bar 1,
• E1 = Young's modulus of bar 1,
• P2, A2, σ2, E2 = Corresponding values of bar 2,
• P = Total load on the composite bar,
• l = Length of the composite bar, and
• δl = Elongation of the composite bar.
• We know that P = P1 + P2
• Stress in bar 1,
• strain in bar 1, 21

22. • Elongation in bar -1:
• Elongation in bar -2:
There fore,
δl1 = δl2
• The ratio E1 / E2 is known as modular ratio of the two materials
22

23. P = P1 + P2
=
=
23

24. δl1 = δl2
P = P1 + P2 = σ1.A1 + σ2.A2
24

25. EX:3
A bar 3 m long is made of two bars, one of copper having
E = 105 GN/m2 and the other of steel having E = 210 GN/m2.
Each bar is 25 mm broad and 12.5 mm thick. This compound
bar is stretched by a load of 50 kN. Find the increase in length
of the compound bar and the stress produced in the steel and
copper. The length of copper as well as of steel bar is 3 m
each.
Ans:
Pc=16.67N
Ps=33.33N
δl=1.52 mm
25

26. EX:4
• A central steel rod 18 mm diameter passes through a
copper tube 24 mm inside and 40 mm outside diameter, as
shown in Fig. It is provided with nuts and washers at each
end. The nuts are tightened until a stress of 10 MPa is set
up in the steel. Find out stress generated in copper tube.
Hint: Ps=Pc
σs × As = σc × Ac

27. BARS WITH CROSS-SECTIONS VARYING IN STEPS
• A typical bar with cross-sections varying in steps and subjected
to axial load
• length of three portions L1, L2 and L3 and the respective cross-
sectional areas are A1, A2, A3
• E = Young’s modulus of the material
• P = applied axial load.
27

28. • forces acting on the cross-sections of the three portions. It
is obvious that to maintain equilibrium the load acting on
each portion is P only.
28

29. Stress, strain and extension of each of these portions are:
Portion Stress Strain Extension
1 σ1 = P/ A1 e1 = σ1 / E δ1 = P L1 / A1 E
2 σ2 = P/ A2 e2 = σ2 / E δ2 = P L2 / A2 E
3 σ3 = P/ A3 e3 = σ3 / E δ3 = P L3 / A3 E
29

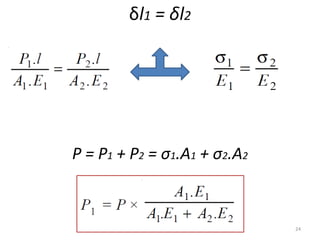
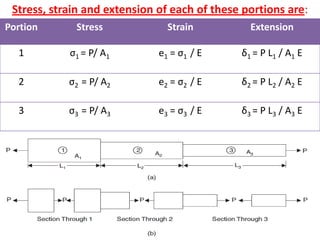
30. Total Elongation: δ
δ1 + δ2 + δ3 = [P L1 / A1 E] + [P L2 / A2 E] + [P L3 / A3 E]
30

31. EX:5
The bar shown in Fig. 8.16 is tested in universal testing
machine. It is observed that at a load of 40 kN the total
extension of the bar is 0.280 mm. Determine the Young’s
modulus of the material.
31

32. Thermal Stresses
 Stresses due to Change in Temperature
 Whenever there is some increase or decrease in the
temperature of a body, it causes the body to expand or
contract.
 If the body is allowed to expand or contract freely, with the rise
or fall of the temperature, no stresses are induced in the body.
 But, if the deformation of the body is prevented, some stresses
are induced in the body. Such stresses are known as thermal
stresses.
32

33. • l = Original length of the body,
• t = Rise or fall of temperature,
• α = Coefficient of thermal expansion,
∴ Increase or decrease in length,
δl = l × α × t
• If the ends of the body are fixed to rigid supports, so that its
expansion is prevented, then compressive strain induced in the
body,
• ∴ Thermal stress,
33

34. If the free expansion is prevented fully
• Since support is not permitting it, the support force P develops
to keep it at the original position.
• Magnitude of this force is such that contraction is equal to free
expansion
δl = l × α × t
34

35. If free expansion is prevented partially
Expansion prevented Δ = α tL – δ
35

36. EX:6: A steel rail is 12 m long and is laid at a temperature of 18°C.
The maximum temperature expected is 40°C.
(i) Estimate the minimum gap between two rails to be left so that
the temperature stresses do not develop.
(ii) Calculate the temperature stresses developed in the rails, if:
(a) No expansion joint is provided.
(b) If a 1.5 mm gap is provided for expansion.
(iii) If the stress developed is 20 N/mm2, what is the gap provided
between the rails?
Take E = 2 × 105 N/mm2 and α = 12 × 10–6/°C.
36

37. Linear and Lateral Strain
• Consider a circular bar of diameter d and length l, subjected to a
tensile force P
• Due to tensile force, the length
of the bar increases by an amount δl
and the diameter decreases by
an amount δd
• Similarly, if the bar is subjected
to a compressive force,
• Every direct stress is accompanied by a strain in its own direction is
known as linear strain and an opposite kind of strain in every
direction, at right angles to it, is known as lateral strain.
37

38. Poisson's Ratio
• When a body is stressed within elastic limit, the lateral strain bears a
constant ratio to the linear strain.
• This constant is known as Poisson's ratio and is denoted by
(1/m) or μ.
38

39. Volumetric Strain
• When a body is subjected to a system of forces, it undergoes some
changes in its dimensions. The volume of the body is changed.
• The ratio of the change in volume to the original volume is known as
volumetric strain.
• Volumetric strain, εv = δV / V ; δV = Change in
volume, ; V = Original
volume.
• Volumetric strain of a rectangular body subjected to an axial force
is given as
• Volumetric strain of a rectangular body subjected to three mutually
perpendicular forces is given by 39

40. Bulk Modulus
• When a body is subjected to three mutually perpendicular
stresses, of equal intensity, then the ratio of the direct stress to the
corresponding volumetric strain is known as BULK MODULUS.
• It is usually denoted by K.
• Bulk modulus,
40

41.  Relation Between Bulk Modulus and Young’s Modulus
 Relation Between Young’s Modulus and Modulus of Rigidity
41

42. EX:7
A bar of 25 mm diameter is tested in tension. It is observed that
when a load of 60kN is applied, the extension measured over a
gauge length of 200 mm is 0.12 mm and contraction in diameter is
0.0045 mm. Find Poisson’s ratio and elastic constants E, G, K.
EX:8
A circular rod of 25 mm diameter and 500 mm long is
subjected to a tensile force of 60 KN. Determine modulus of
rigidity, bulk modulus and change in volume if Poisson’s ratio
= 0.3 and Young’s modulus E = 2 × 105 N/mm2.
42

43. EX:9 A 400 mm long bar has rectangular cross-section 10 mm × 30
mm. This bar is subjected to
(i) 15 kN tensile force on 10 mm × 30 mm faces,
(ii) 80 kN compressive force on 10 mm × 400 mm faces, and
(iii) 180 kN tensile force on 30 mm × 400 mm faces.
Find the change in volume if E = 2 × 105 N/mm2 and μ = 0.3.
43

44. Stress concentration
• Whenever a machine component changes the shape of its cross-
section, the simple stress distribution no longer holds good.
• This irregularity in the stress distribution caused by abrupt changes of
form is called stress concentration.
• It occurs for all kinds of stresses in the presence of
fillets, notches, holes, keyways, splines, surface roughness or
scratches etc.
44

45. Thank You…
45