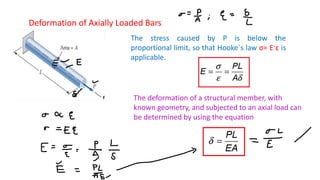
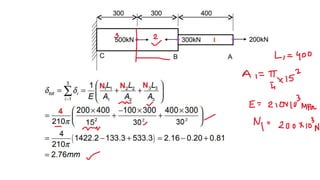
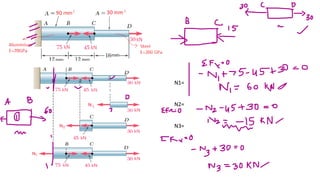
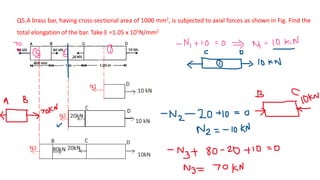
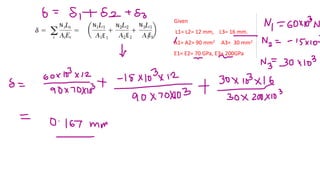The document discusses deformation of axially loaded bars. It defines key terms like stress, strain, Hooke's law, stiffness, compliance, and axial rigidity. It also describes how to calculate deformation of bars with multiple loads or non-uniform properties by dividing the bar into segments and using the principle of superposition. Several example problems are given to illustrate calculating deformation of bars under different loading conditions.

2. Deformation of Axially Loaded Bars
The stress caused by P is below the
proportional limit, so that Hooke`s law σ= E·ε is
applicable.
The deformation of a structural member, with
known geometry, and subjected to an axial load can
be determined by using the equation

3. The term EA/L is the stiffness of the member so we can rewrite the equation as
Parameter k is called stiffness (or spring constant). The
reciprocal of the stiffness, k-1, is called compliance.
The product EA is known as the axial rigidity of the bar.

4. Q1. The tie-rods in the press in Figure are made of the steel alloy SAE 5160 OQT 900. Each
rod has a diameter of 50.0 mm and an initial length of 1740 mm. An axial tensile load of
180 kN is exerted on each rod during operation of the press. Compute the deformation of
the rods. Take E = 207 GPa.
Diameter = D = 50.0 mm,
Length = L = 1740 mm,
Axial force = F = 180 kN.
E = 207 GPa.
Area=
Tensile stress=
Axial deformation=

5. Q2. A large pendulum is composed of a 10.0 kg ball suspended by an aluminum wire
having a diameter of 1.00 mm and a length of 6.30 m. The aluminum is the alloy 7075-T6.
Compute the elongation of the wire due to the weight of the 10 kg ball.

7. Force on the wire: F = w = m · g = (10.0 kg)(9.81 m/s2) = 98.1 N.

8. Deformation for Bars Carrying Multiple Loads or Having Differing
Properties
When any factor in the Equation is different over the length of a given member, the
member must be divided into segments for which all factors are the same.
Then, you can use superposition to determine the total deformation of the member.

9. Deformation for Bars Carrying Multiple Loads or Having Differing
Properties
Bar with external loads
acting at intermediate
points
Bar consisting of prismatic
segments having different axial
forces, different dimensions,
and different materials
Bar consisting of prismatic segments
having different axial forces,
different dimensions

10. The principle of superposition states that when multiple loads are
acting on a bar , the change in length of this bar is found by adding
algebraically the elongations and shortenings of the individual
segments.
• Identify the segments of the bar
• Determine the internal axial forces N1, N2, and N3 in segments 1, 2, and 3, respectively, from the free-body
diagrams.
• Determine the changes in the lengths of the segments
• Add δ1, δ2, and δ3 to obtain δ, the change in length of the entire bar:

11. Q3.The two-step steel rod is subjected to the three external loads shown. The large
and small sections of the rod have a diameter of 30 mm and 15 mm respectively.
Young’s modulus for steel is 210 GPa. Calculate the elongation of the rod.
First Step: We need to determine the actual loads experienced by the rod in each part of the assembly
How do we do this?
How many free body diagrams?

14. Q4.Determine the deformation of the rod shown in Figure, given loads

15. N1=
N2=
N3=

16. Given
L1= L2= 12 mm, L3= 16 mm.
A1= A2= 90 mm2 A3= 30 mm2
E1= E2= 70 GPa, E3= 200GPa

17. Q5.A brass bar, having cross-sectional area of 1000 mm2, is subjected to axial forces as shown in Fig. Find the
total elongation of the bar. Take E =1.05 x 105N/mm2

18. Q5.A brass bar, having cross-sectional area of 1000 mm2, is subjected to axial forces as shown in Fig. Find the
total elongation of the bar. Take E =1.05 x 105N/mm2

20. Q5. A member ABCD is subjected to point loads P1, P2, P3 andP4 as shown in Fig. Calculate the
force P2 necessary for equilibrium, P1= 45 kN, P3= 450 kN and P4 = 130 kN. Determine the total
elongation of the member, assuming the modulus of elasticity to be 2.1 x 105 N/mm2

21. Q5. A member ABCD is subjected to point loads P1, P2, P3 andP4 as shown in Fig. Calculate the
force P2 necessary for equilibrium, P1= 45 kN, P3= 450 kN and P4 = 130 kN. Determine the total
elongation of the member, assuming the modulus of elasticity to be 2.1 x 105 N/mm2

22. Q5. A member ABCD is subjected to point loads P1, P2, P3 andP4 as shown in Fig. Calculate the
force P2 necessary for equilibrium, P1= 45 kN, P3= 450 kN and P4 = 130 kN. Determine the total
elongation of the member, assuming the modulus of elasticity to be 2.1 x 105 N/mm2

23. Q5. A member ABCD is subjected to point loads P1, P2, P3 andP4 as shown in Fig. Calculate the
force P2 necessary for equilibrium, P1= 45 kN, P3= 450 kN and P4 = 130 kN. Determine the total
elongation of the member, assuming the modulus of elasticity to be 2.1 x 105 N/mm2

24. Q5. A member ABCD is subjected to point loads P1, P2, P3 andP4 as shown in Fig. Calculate the
force P2 necessary for equilibrium, P1= 45 kN, P3= 450 kN and P4 = 130 kN. Determine the total
elongation of the member, assuming the modulus of elasticity to be 2.1 x 105 N/mm2