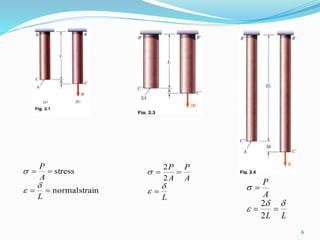
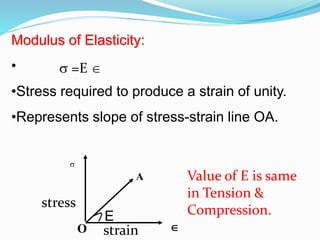
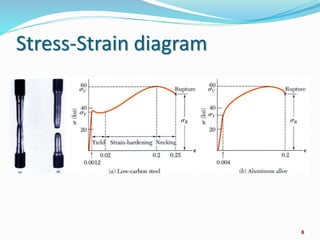
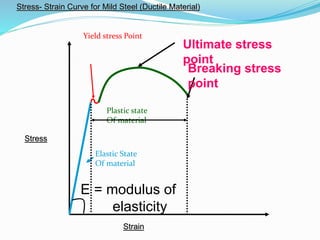
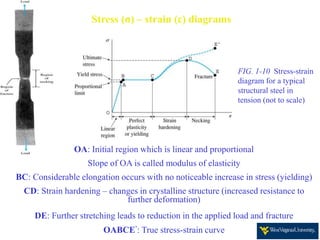
This document provides an overview of topics related to simple stresses and strains, including: - Types of stresses and strains such as tensile, compressive, direct stress, and direct strain. - Hooke's law and how stress is proportional to strain below the material's yield point. - Stress-strain diagrams and key points such as the elastic region, yield point, and fracture point. - Definitions of terms like working stress, factor of safety, Poisson's ratio, and elastic moduli. - Examples of problems calculating stresses, strains, extensions, and deformations of simple structural members under various loads.

1. Unit -1
Simple Stresses
&
Strains

2. Topics
 Types of stresses & strains,
 Hooke’s law, stress-strain diagram,
 Working stress,
 Factor of safety,
 Lateral strain,
 Poisson’s ratio, volumetric strain,
 Elastic moduli,
 Deformation of simple and compound bars under axial
load,
 Analysis of composite bar with varying cross section.
2

3. Types of Stresses & Strains
3
Direct Stress (σ)
When a force is applied to an elastic body, the body deforms. The way in
which the body deforms depends upon the type of force applied to it.
Compressive Stress due to compressive force
A Compression force makes the body shorter.
Tensile Stress due to tensile force
A tensile force makes the body longer

4. 4
• Resistance offered by the material per unit cross- sectional
area is called STRESS
• Tensile and compressive forces are called DIRECT FORCES
• Stress is the force per unit area upon which it acts.
A
F
Area
Force
Stress   2
/ mN or Pascal (Pa)
Note: Most of engineering fields used kPa, MPa, GPa.
( σ is called as Sigma)

5. 5
Direct Strain (ε) Also called as Longitudinal Strain
In each case, a force ‘F’ produces a deformation ‘x’ . In engineering, we
usually change this force into stress and the deformation into strain and
we define these as follows:
• Strain is the deformation per unit of the original length.
Strain, ε = ΔL/L = Change in length/ Original length
(ε is called as Epsilon)
• Strain has no unit’s since it is a ratio of length to length
L DL

6. 6
strainnormal
stress


L
A
P



L
A
P
A
P





2
2
LL
A
P





2
2

7. Hooke’s law
7
Below the yield stress
Stress α Strain (ie) σ α ε
σ = E ε
Where E is a constant called as
Youngs Modulus or Modulus of Elasticity

8. Stress-Strain diagram
8

9. Strain
Stress
Stress- Strain Curve for Mild Steel (Ductile Material)
Plastic state
Of material
Elastic State
Of material
Yield stress Point
E = modulus of
elasticity
Ultimate stress
point
Breaking stress
point

10. Stress (σ) – strain (ε) diagrams
OA: Initial region which is linear and proportional
Slope of OA is called modulus of elasticity
BC: Considerable elongation occurs with no noticeable increase in stress (yielding)
CD: Strain hardening – changes in crystalline structure (increased resistance to
further deformation)
DE: Further stretching leads to reduction in the applied load and fracture
OABCE’: True stress-strain curve
FIG. 1-10 Stress-strain
diagram for a typical
structural steel in
tension (not to scale)

11. 11

12. Working stress
 The stress to which the material may be safely subjected in the
course of ordinary use. Also called as Allowable Load or
Allowable stress
 Max load that a structural member/machine component
will be allowed to carry under normal conditions of
utilisation is considerably smaller than the ultimate load
 This smaller load = Allowable load / Working load / Design
load
 Only a fraction of ultimate load capacity of the member is
utilised when allowable load is applied
 The remaining portion of the load-carrying capacity of the
member is kept in reserve to assure its safe performance
12

13. Factor of safety
13

14. Elastic moduli
14

15. Modulus of Elasticity:
•
•Stress required to produce a strain of unity.
•Represents slope of stress-strain line OA.
A


O
stress
strain
Value of E is same
in Tension &
Compression.
 =E 
E

16. A


O
• Hooke’s Law:-
Up to elastic limit, Stress is proportional to strain
  
 =E ; where E=Young’s modulus
=P/A and  =  / L
P/A = E ( / L)
 =PL /AE
E

17. Volumetric Strain . . . .
17
Also we know that

18. Problems
18

19. Deformation of simple
and
compound bars
under
axial load
19

20. 1. An elastic rod of 25mm in diameter, 200mm long
extends by 0.25mm under a tensile load of 40KN.
Find the intensity of stress, the strain and the elastic
modulus for the material of the rod.
20

21. 2. Find the maximum and minimum stresses produced
in the stepper bar of 12mm and 25mm diameter
shown in Figure due to an axially applied
compressive load od 12KN.
21

22. 3. A steel rod of 25mm in diameter and 2M long is
subjected to an axial pull of 45KN. Find
i. The intensity of stress
ii. The strain and
iii. Elongation. Take E= 2x105 N/mm2
22

23. 4. A load of 4000N has to be raised at the end of a steel
wire. If the unit stress in the wire must not exceed
80N/mm2 , what is the minimum diameter required?
What will be the extension of 3.50M length of wire?
Take E = 2 x 105 N/mm2
23

24. 5. A 20mm diameter brass rod was subjected to a
tensile load of 40KN. The extension of the rod was
found to be 254 divisions in the 200mm extension
meter. If each division is equal to 0.001mm, find the
elastic modulus of brass.
24

25. 6. A hollow steel column has an external diameter of
250mm and an internal diameter of 200mm. Find the
safe axial compressive load for the column, if the safe
compressive stress is 120 N/mm2
25

26. 7. A hollow steel column of external diameter 250mm
has to support an axial load of 2000KN. If the
Ultimate stress for the steel column is 480N/mm2 ,
find the internal diameter of the column allowing a
load factor of 4.
26

27. 8. The following data refer to a mild steel specimen
tested in a laboratory:
Diameter of the specimen = 25mm; Length of the
specimen = 300mm; Extension at the load of 15KN =
0.045mm; Load at the yield point = 127.65KN;
Max. Load = 208.60KN; Length of the specimen after the
failure = 375mm; Neck dia. = 17.75mm
Find E, Yield point stress, Ultimate stress,
% of elongation, % of reduction in area, Safe stress
adopting a FOS of 2.
27

28. Analysis of composite bar with
varying cross section
28

29. Bars of Varying cross-Section
29

30. 9. A bar ABCD 950mm long is made up of 3 parts AB,
BC and CD of lengths 250mm, 450mm, 250mm
respectively. The part BC is in square section of
30mm x 30mm. The rod is subjected to a pull of
26000N. Find the stresses in 3 parts, extension of the
rod. Take E = 2 x 105 N/mm2 .
30

31. 10. A brass bar having a cross sectional area of 1000 mm2
is subjected to axial forces as shown in figure. Find
the total change of length of the bar.
Take E= 1.05 x 105 mm2
31

32. 11. A member ABCD is subjected to point loads P1 ,P2 ,P3
and P4 as shown in Figure. Calculate the force P3
necessary for equilibrium if P1 = 120KN, P2 = 220KN
and P4 = 160KN. Also determine the net change in
length of the member. Take E = 2 x 105 N/mm2 .
32

33. Composite Bar
33
Brass
Steel

34. 12. A compound tube consists of a steel tube of 150mm
ID & 10mm thickness and an outer brass tube of
170mm ID & 10mm thickness. The two tubes are of
the same length. The compound tubes carries an
axial load of 1000KN. Find the stresses and the load
carried by each tube and the amount it shortens.
Length of each tube is 150mm. Take E for steel= 2 x
105 N/mm2 and E for Brass= 1 x 105 N/mm2
34

35. Lateral strain
 "The strain at right angles to the direction of
applied load is known as LATERAL STRAIN."
(OR)
 "Change in breadth dimensions to original
dimension is also known as LATERAL STRAIN"
 𝑳𝒂𝒕𝒆𝒓𝒂𝒍 𝑺𝒕𝒓𝒂𝒊𝒏 =
𝑪𝒉𝒂𝒏𝒈𝒆 𝒊𝒏 𝑳𝒂𝒕𝒆𝒓𝒂𝒍 𝒅𝒊𝒎𝒆𝒏𝒔𝒊𝒐𝒏𝒔
𝑶𝒓𝒊𝒈𝒊𝒏𝒂𝒍 𝒅𝒊𝒎𝒆𝒏𝒔𝒊𝒐𝒏𝒔
35

36. Poisson’s ratio
36

37. Volumetric strain
 It is the unit change in volume due to a deformation. It
is an important measure of deformation.
37
Consider a rectangular solid of sides x, y and z
under the action of principal stresses σ1 , σ2 , σ3
respectively.
Then ε1 , ε2 , and ε3 are the corresponding linear
strains, than the dimensions of the rectangle
and it becomes
( x + ε1 . x ); ( y + ε2 . y ); ( z + ε3 . z )

38. 13. A steel bar of 50mm wide, 12mm thick and 300mm
long is subjected to an axial pull of 84KN. Find the
changes in length, width, thickness and volume of
the bar. Take E = 2 x 105 and Poisson’s ratio = 0.32
38

39. 14. A steel rod 4m long and 20mm diameter is subjected
to an axial tensile load of 45KN. Find the change in
length, diameter and the volume of the rod. Take E =
2 x 105 N/mm2 and Poisson’s ratio = 0.25
39

40. Thank you
for your attention
40