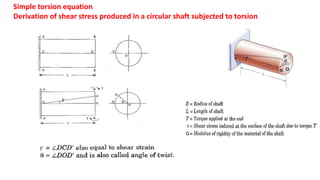
The document discusses torsion in shafts. When equal and opposite torques are applied to the ends of a shaft, it experiences twisting and shear stresses. For a circular shaft under torsion, every cross-section remains undistorted due to symmetry. Shear stress is highest at the outer surface and lowest at the axis. The maximum torque a circular solid shaft can transmit depends on the shear stress limit and material properties. Polar modulus is a measure of a shaft's resistance to twisting. Torsional rigidity describes a shaft's resistance to twisting deformation.

2. A shaft is said to be in torsion, when equal and opposite
torques are applied at the two ends of the shaft. Due to
the application of the torques at the two ends, the shaft
is subjected to a twisting moment. This causes the shear
stresses and shear strains in the material of the shaft.
 The torque is equal to the product of the force applied
(tangentially to the ends of a shaft) and radius of the
shaft.

3. When subjected to torsion, every cross-section of
circular (solid or hollow) shaft remains plane and
undistorted. This is due to axisymmetry of cross section.
 Cross-sections of noncircular shafts are distorted when
subjected to torsion – since no axisymmetry.

4. Simple torsion equation
Derivation of shear stress produced in a circular shaft subjected to torsion

6. The shear stress is maximum at the outer surface and shear
stress is zero at the axis of the shaft.
𝜏 =
𝑮𝜽
𝑳
R

7. MAXIMUM TORQUE TRANSMITTED BY A CIRCULAR SOLID SHAFT

8. 𝑇 =
𝜏
𝑅
𝛱
2
𝑅4
𝑇 =
𝜏
𝑅
(
𝛱
32
𝐷4)
𝑻
𝑱
=
𝝉
𝑹
=
𝑮𝜽
𝑳
Simple Torsion Equation

9. POLAR MODULUS
Polar modulus is defined as the ratio of the polar moment of inertia to the
radius of the shaft. It is also called torsional section modulus. It is denoted by
Zp
Zp =
J
𝐑

10. Polar section modulus for a solid shaft
Polar section modulus for a hollow shaft

11. STRENGTH OF A SHAFT AND TORSIONAL RIGIDITY
The strength of a shaft means the maximum torque or maximum
power the shaft can transmit.
Torsional rigidity or stiffness of the shaft is defined as the product of
modulus of Rigidity (G) and polar moment of inertia of the shaft(J).
Torsional Rigidity = G. J
Torsional rigidity is also defined as the torque required to produce a twist of one radian per unit length
of the shaft.

12. Torsional stiffness
The resistance offered by the loaded member to torsional deflection or
twisting is referred to as torsional stiffness.

13. Q2. A solid shaft of 150 mm diameter is used to transmit torque. Find the
maximum torque transmitted by the shaft if the maximum shear stress induced to
the shaft is 45N/mm2
𝑇 = 𝑧 𝑝 𝜏

14. Q2. The shearing stress in a solid shaft is not to exceed 40 N/mm2 when the torque
transmitted is 20000 N-m. Determine the minimum diameter of the shaft.

15. Q3. In a hollow circular shaft of outer and inner diameters of 20 cm and 10 cm
respectively, the shear stress is not to exceed 40 N/mm2 . Find the maximum
torque which the shaft can safely transmit.

16. Assumptions in simple torsion equation:
1.The material of the shaft is uniform throughout.
2. The twist along the shaft is uniform.
3. The shaft is of uniform circular section throughout.
4. Cross-sections of the shaft, which are plane before twist remain
plane after twist.
5. All radii which are straight before twist remain straight after twist.