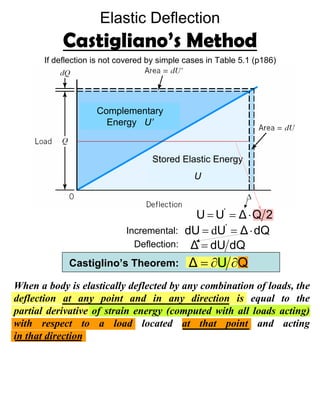
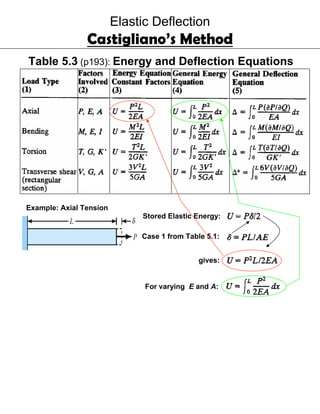
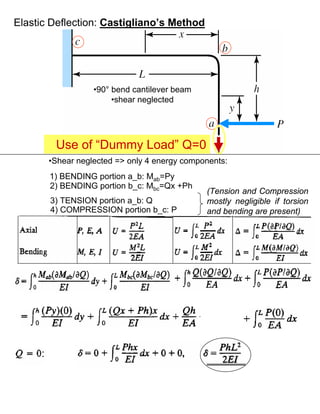
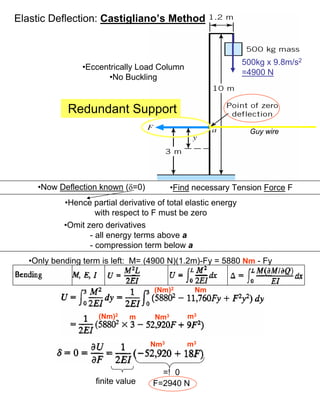
This document discusses Castigliano's theorem for calculating deflections in elastic structures. Castigliano's theorem states that the deflection of a point on a structure due to a load is equal to the partial derivative of the total strain energy with respect to that load. The document provides examples of using Castigliano's theorem to calculate deflections for structures undergoing bending, shear, tension, and compression. It also discusses using a "dummy load" and setting the partial derivative of energy to the load equal to zero to solve for an unknown force.

1. Elastic Deflection
Castigliano’s Method
If deflection is not covered by simple cases in Table 5.1 (p186)
Stored Elastic Energy
U
Complementary
Energy U’
2Q∆UU '
⋅==
dQ∆UdU '
⋅== dIncremental:
dQdU∆ =Deflection:
Castiglino’s Theorem:
When a body is elastically deflected by any combination of loads, the
deflection at any point and in any direction is equal to the
partial derivative of strain energy (computed with all loads acting)
with respect to a load located at that point and acting
in that direction
QU∆ ∂∂=
http://www.egr.msu.edu/classes/me471/thompson/

2. Elastic Deflection
Castigliano’s Method
Table 5.3 (p193): Energy and Deflection Equations
Example: Axial Tension
Stored Elastic Energy:
Case 1 from Table 5.1:
gives:
For varying E and A:
http://www.egr.msu.edu/classes/me471/thompson/

3. Elastic Deflection
Castigliano’s Method
(1) Obtain expression for all components of energy
Table 5.3
(2) Take partial derivative to obtain deflection
QU∆ ∂∂=Castiglino’s Theorem:
Table 5.3 (p193): Energy and Deflection Equations
http://www.egr.msu.edu/classes/me471/thompson/

4. Elastic Deflection: Castigliano’s Method
Table 5.3
Here 2 types of loading: Bending and Shear
magnitude @ x:
1. Energy: here it has two components:
first compute Energy, then Partial Derivative to get deflection
2. Partial Derivatives for deflection:
(23=8)*3*4 = 96
http://www.egr.msu.edu/classes/me471/thompson/

5. Table 5.3
Elastic Deflection: Castigliano’s Method
TWO METHODS
Differentiate after Integral Differentiate under Integral
http://www.egr.msu.edu/classes/me471/thompson/

6. Elastic Deflection: Castigliano’s Method
Transverse shear contributes only <5% to deflection
m
m
http://www.egr.msu.edu/classes/me471/thompson/

7. Elastic Deflection: Castigliano’s Method
Use of “Dummy Load” Q=0
•90° bend cantilever beam
•shear neglected
•Shear neglected => only 4 energy components:
1) BENDING portion a_b: Mab=Py
2) BENDING portion b_c: Mbc=Qx +Ph
3) TENSION portion a_b: Q
4) COMPRESSION portion b_c: P
(Tension and Compression
mostly negligible if torsion
and bending are present)
:
http://www.egr.msu.edu/classes/me471/thompson/

8. Elastic Deflection: Castigliano’s Method
•Eccentrically Load Column
•No Buckling
Redundant Support
500kg x 9.8m/s2
=4900 N
•Now Deflection known (δ=0) •Find necessary Tension Force F
Guy wire
•Hence partial derivative of total elastic energy
with respect to F must be zero
•Omit zero derivatives
- all energy terms above a
- compression term below a
•Only bending term is left: M= (4900 N)(1.2m)-Fy = 5880 Nm - Fy
=! 0
finite value F=2940 N
(Nm)2
m Nm3 m3
(Nm)2 Nm
Nm3 m3
http://www.egr.msu.edu/classes/me471/thompson/