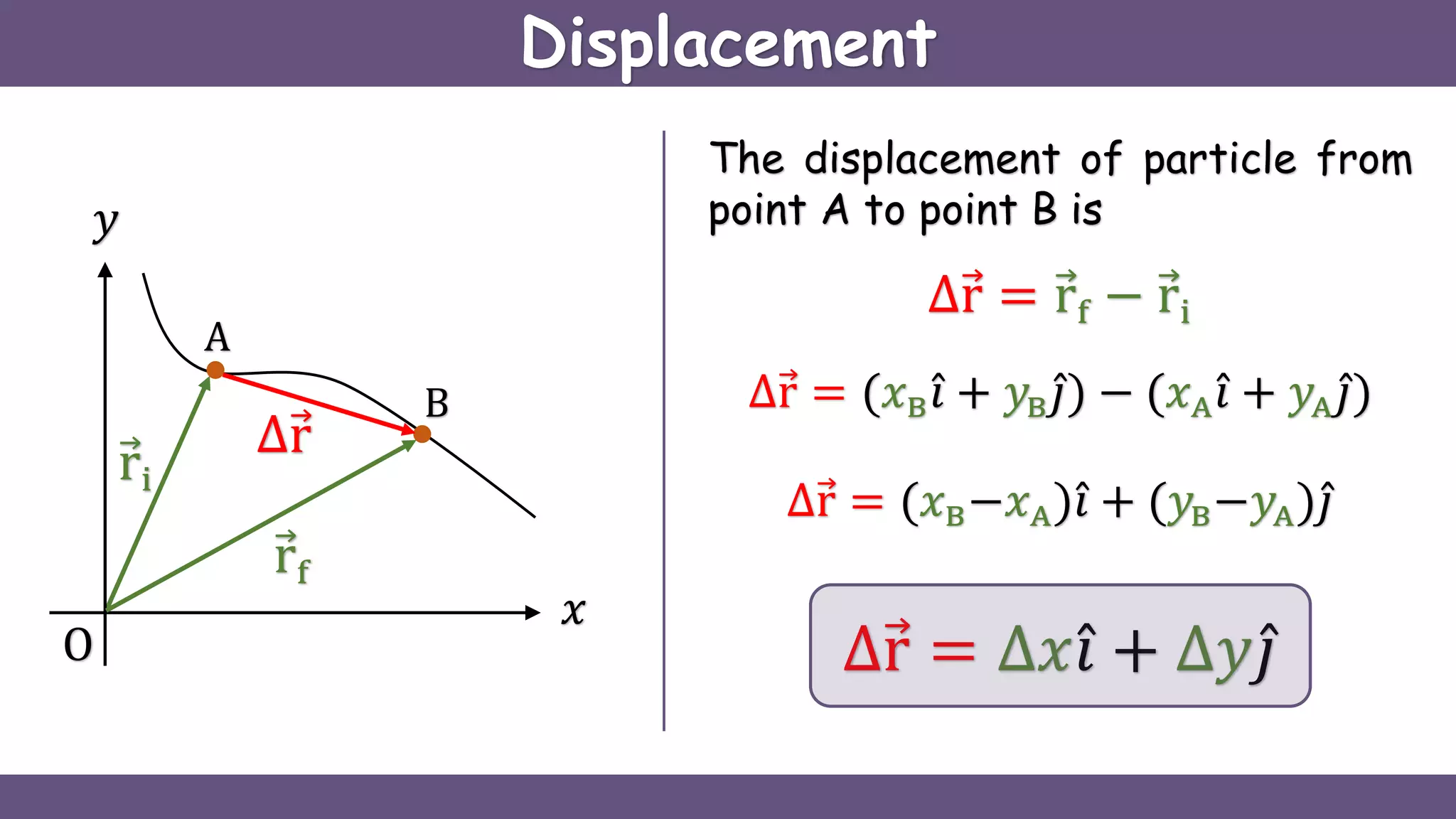
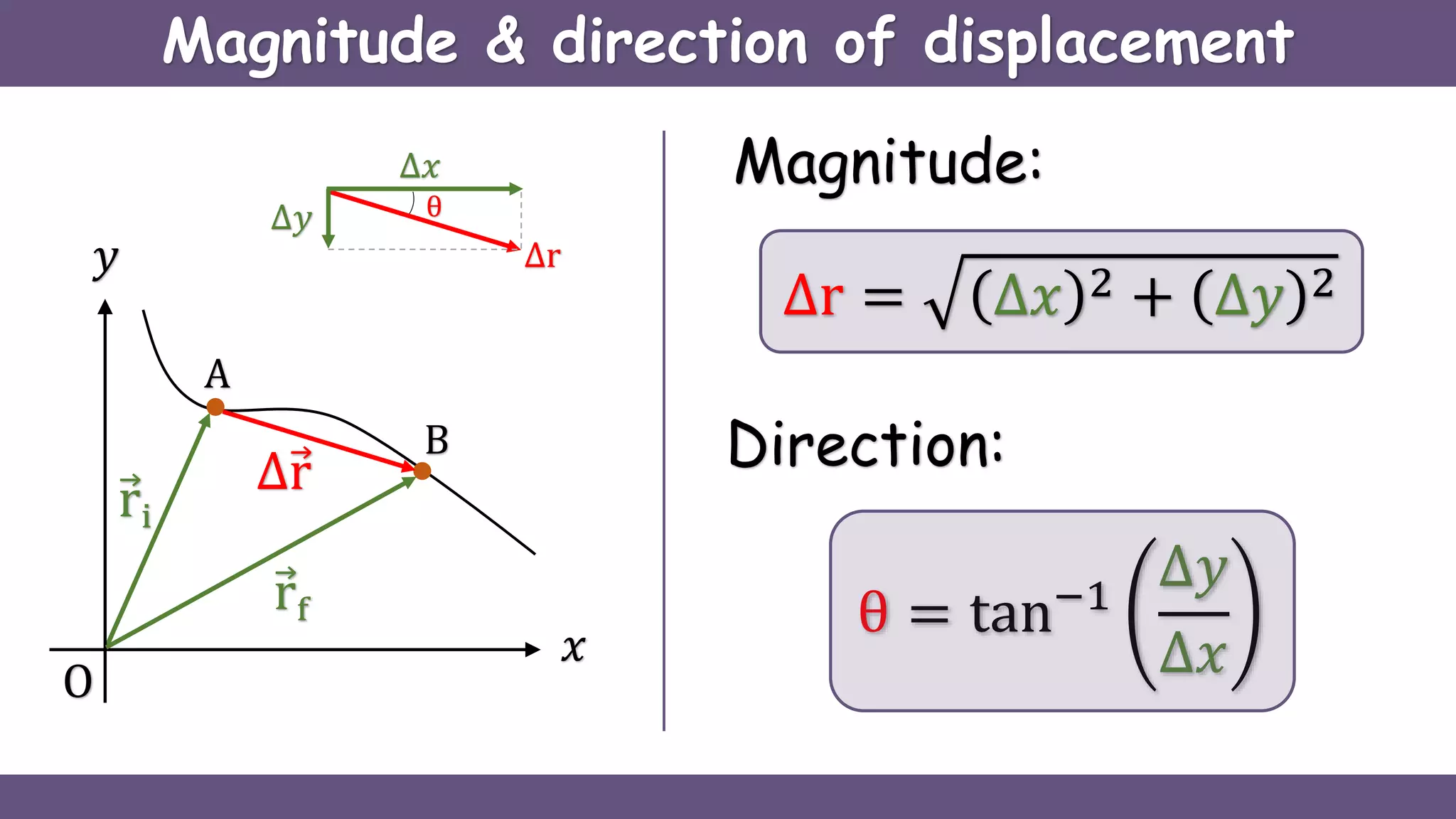
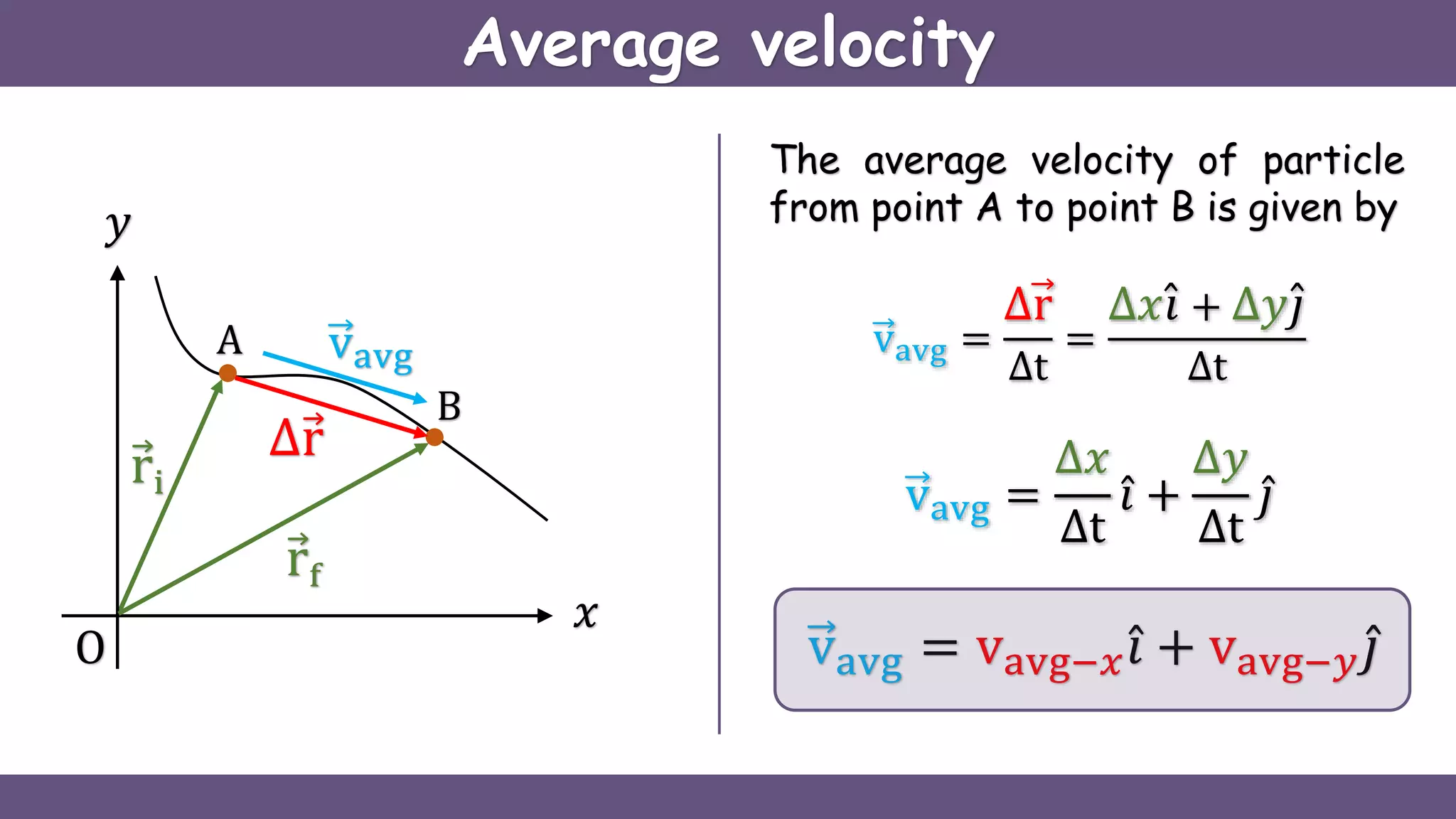
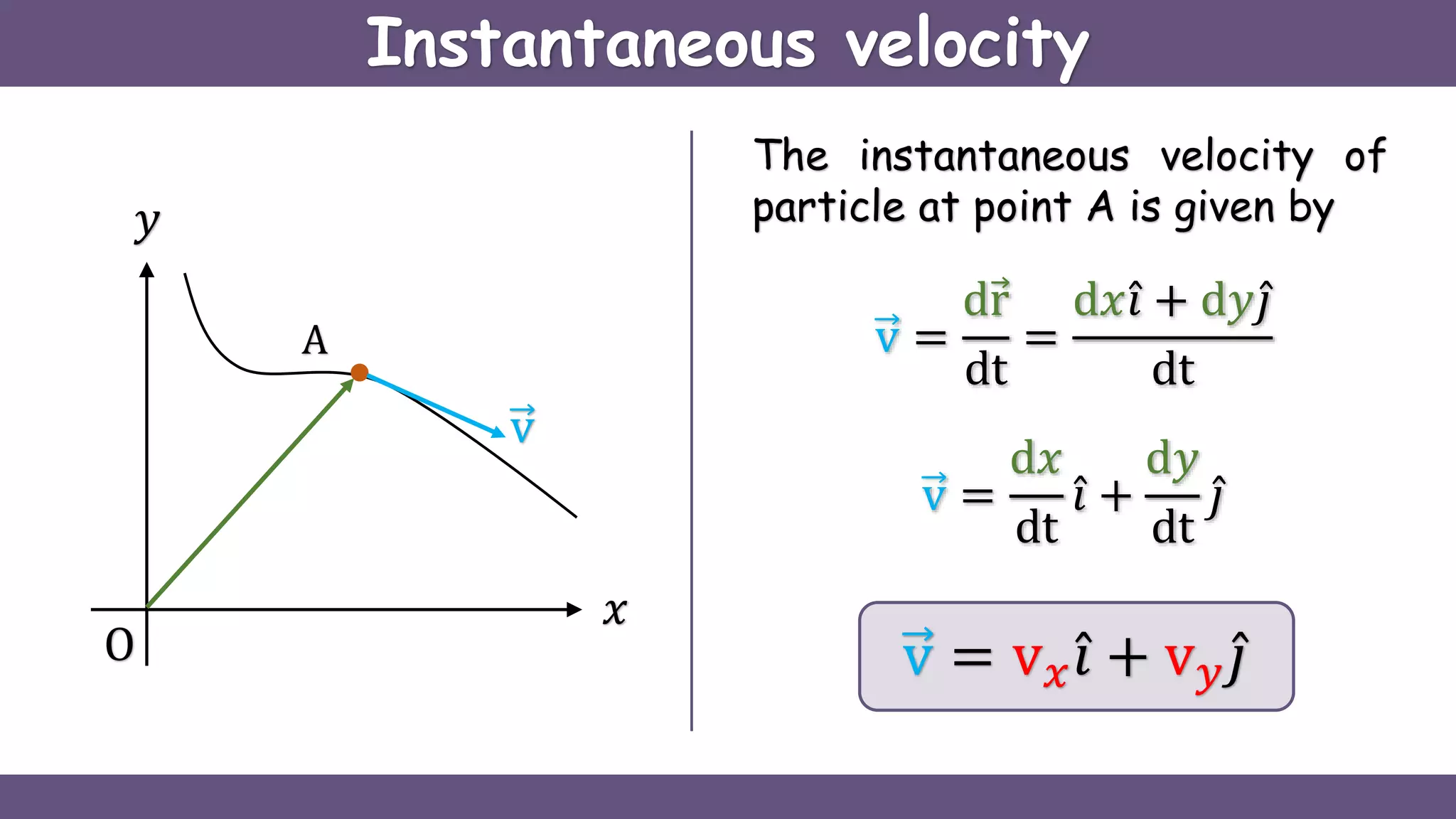
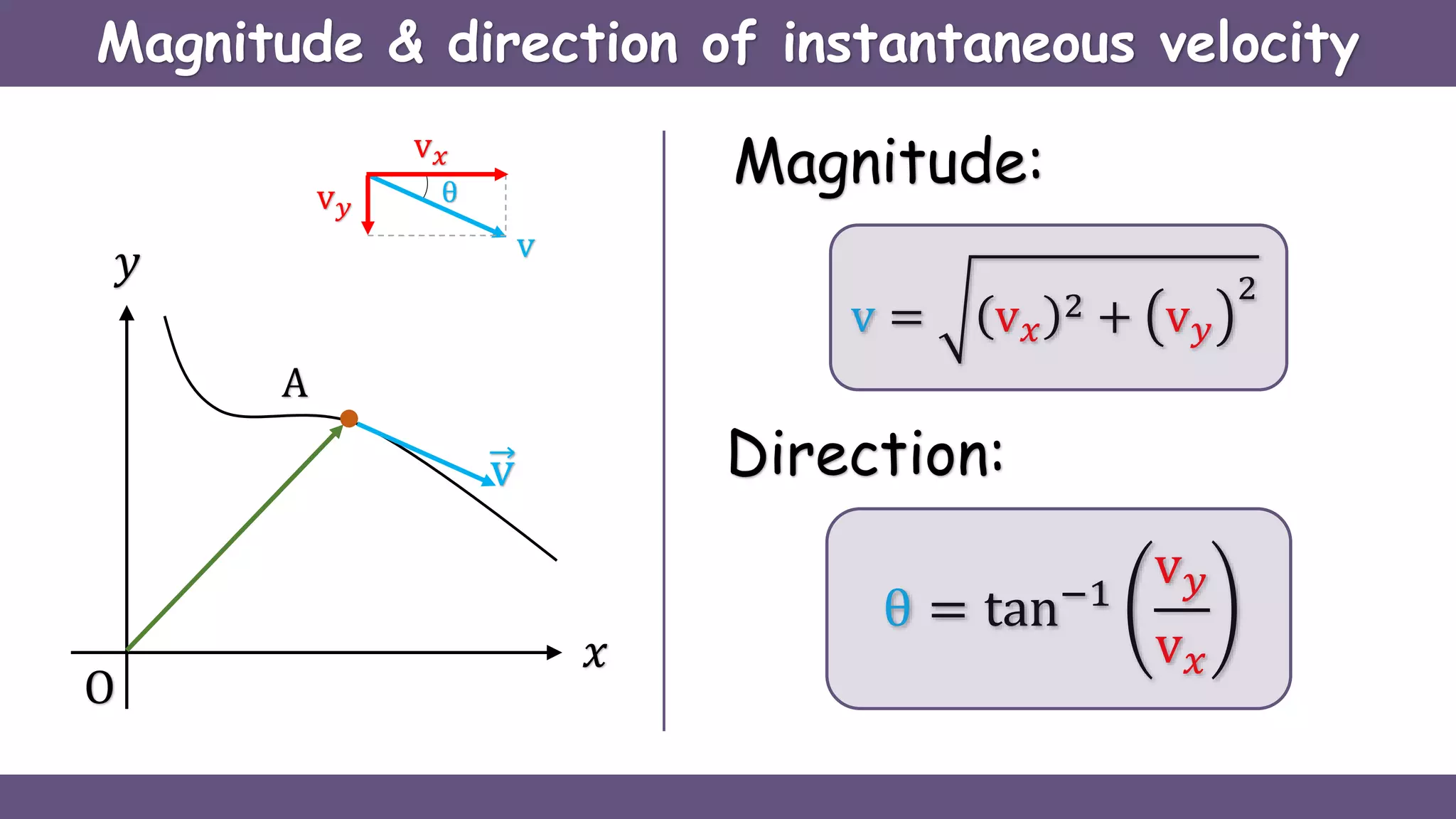
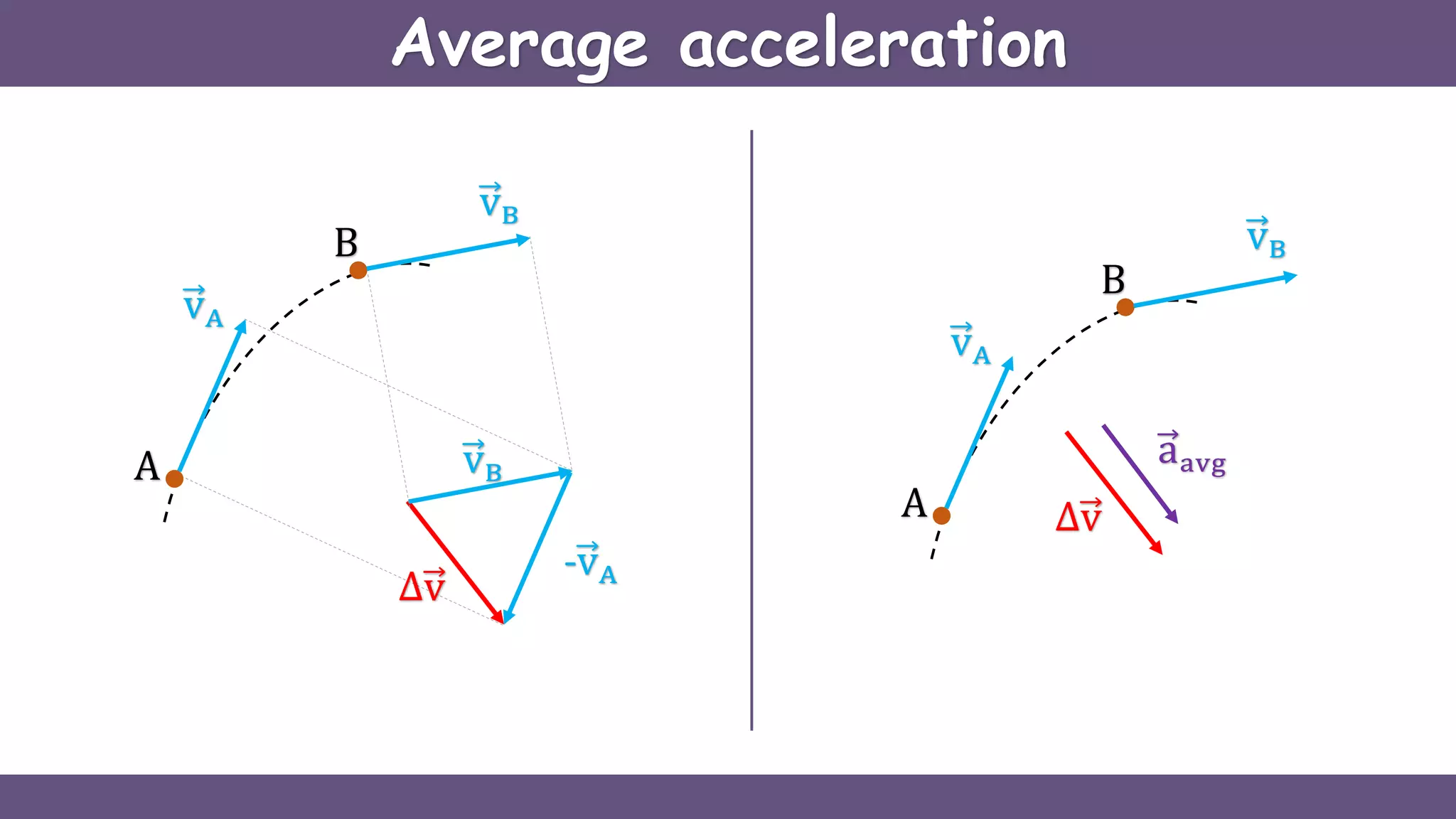
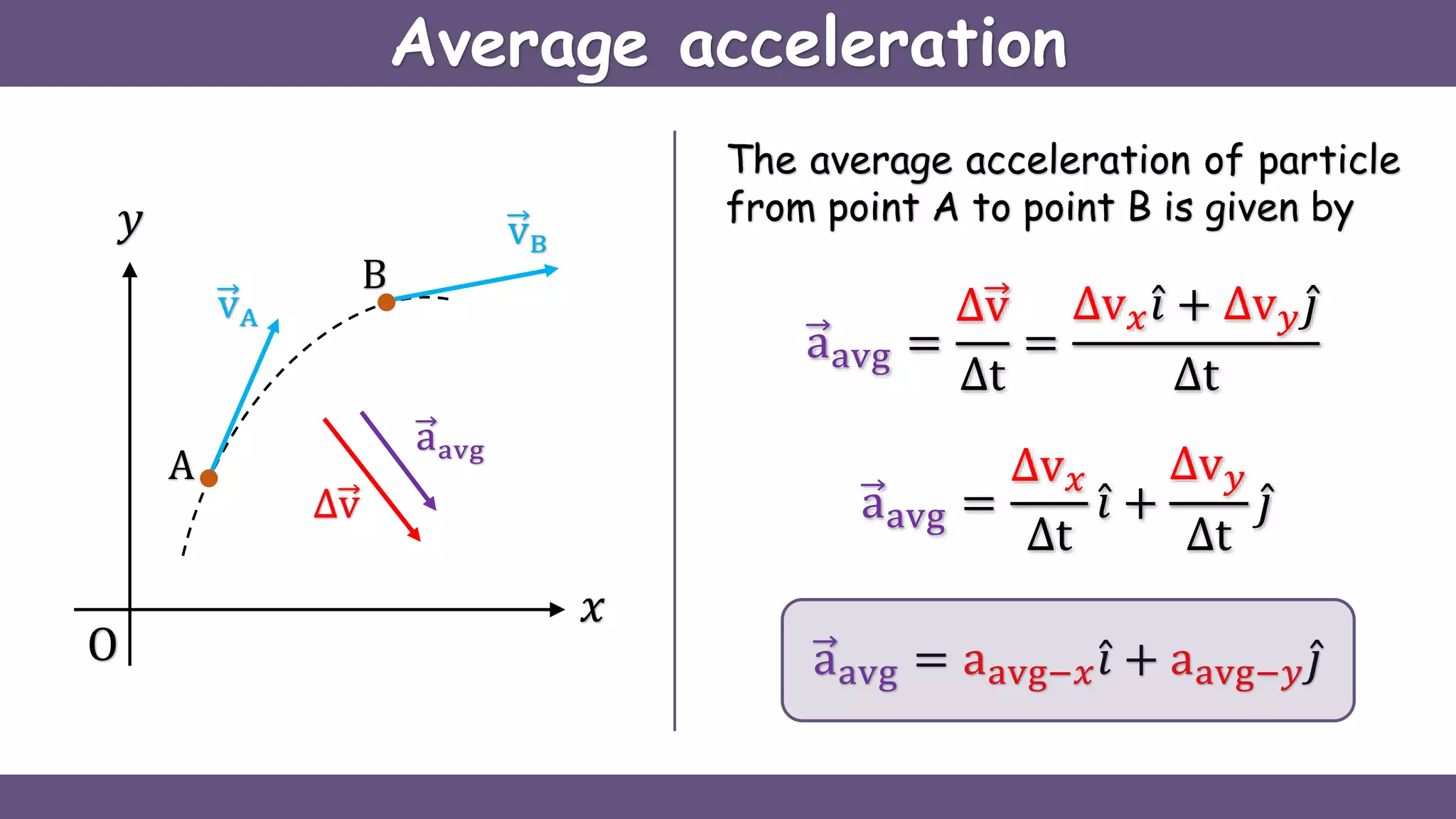
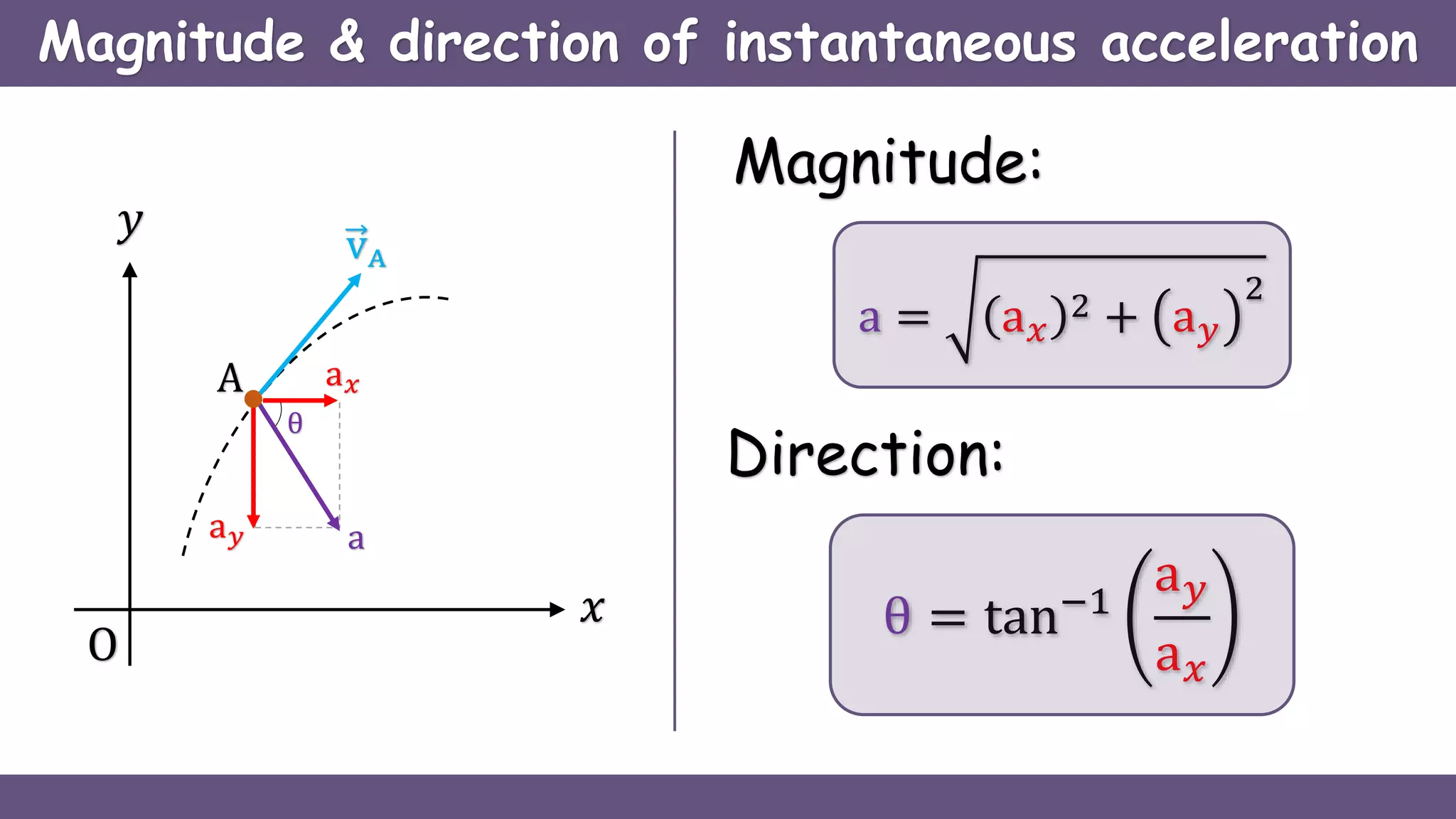
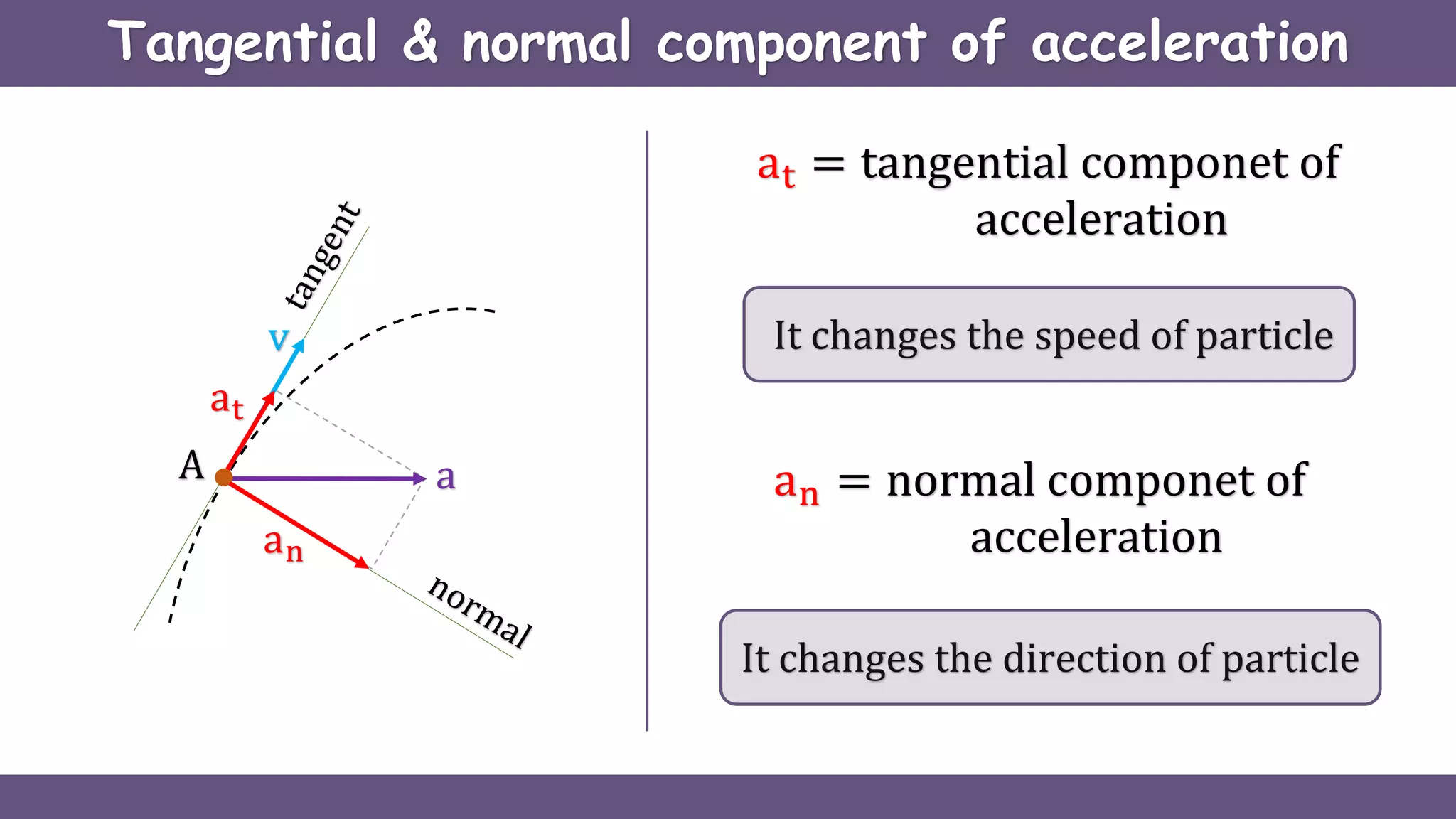
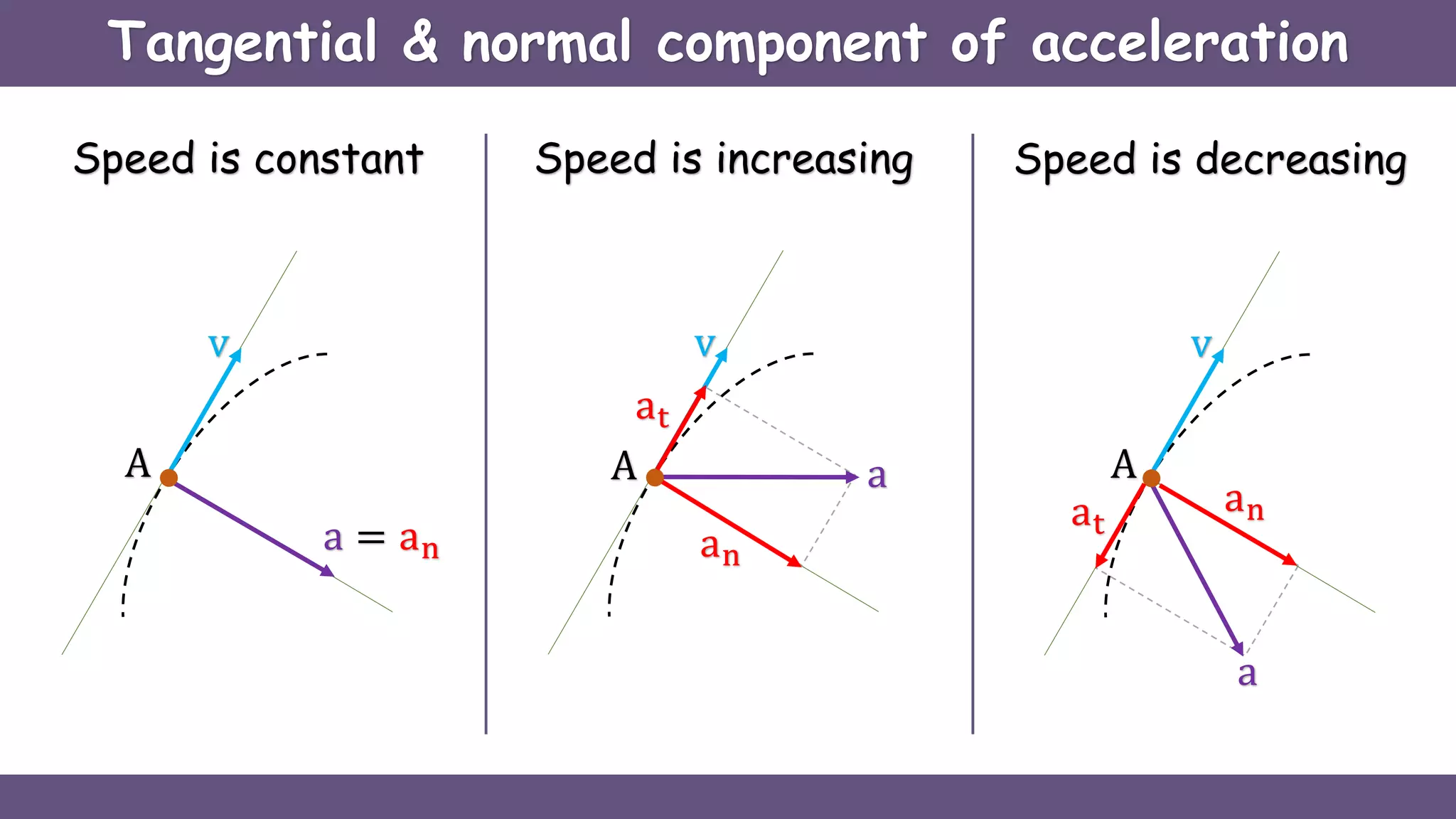
Curvilinear motion refers to the movement of objects along curved paths, exemplified by cars on winding roads or roller coasters on their tracks. The document explains vector representations for displacement, average velocity, instantaneous velocity, average acceleration, and instantaneous acceleration, along with their magnitudes and directions. It also distinguishes between tangential and normal components of acceleration, focusing on how they influence speed and direction.

1. CURVILINEAR
MOTION

2. The motion of an object along
a curved path is called
a curvilinear motion.
Curvilinear motion

3. Motion of car along a
curved road
Motion of cable car along a
steel cable
Curvilinear motion in a plane

4. Motion of roller coaster along
its track.
Motion of fighter jets during
national parade.
Curvilinear motion in a space

5. Position
r
𝑥 𝑖O
𝑥
𝑦
𝑦 𝑗
A r = 𝑥 𝑖 + 𝑦 𝑗
The position of particle at point A
in vector form is represented as,
The distance of particle from
origin is
r = 𝑥2 + 𝑦2
Particle′s path

6. Displacement
ri
O
𝑥
𝑦
A
B
rf
∆r
The displacement of particle from
point A to point B is
∆r = rf − ri
∆r = (𝑥B 𝑖 + 𝑦B 𝑗) − (𝑥A 𝑖 + 𝑦A 𝑗)
∆r = (𝑥B−𝑥A) 𝑖 + (𝑦B−𝑦A) 𝑗
∆r = ∆𝑥 𝑖 + ∆𝑦 𝑗

7. Magnitude & direction of displacement
ri
O
𝑥
𝑦
A
B
rf
∆r
Magnitude:
∆r
∆𝑥
∆𝑦 θ
∆r = ∆𝑥 2 + ∆𝑦 2
Direction:
θ = tan−1
∆𝑦
∆𝑥

8. Average velocity
ri
O
𝑥
𝑦
A
B
rf
∆r
The average velocity of particle
from point A to point B is given by
vavg vavg =
∆r
∆t
=
∆𝑥 𝑖 + ∆𝑦 𝑗
∆t
vavg =
∆𝑥
∆t
𝑖 +
∆𝑦
∆t
𝑗
vavg = vavg−𝑥 𝑖 + vavg−𝑦 𝑗

9. Magnitude & direction of average velocity
ri
O
𝑥
𝑦
A
B
rf
∆r
vavg
Magnitude:
vavg = vavg−𝑥
2
+ vavg−𝑦
2
Direction:
θ = tan−1
vavg−𝑦
vavg−𝑥
vavg
vavg−𝑥
vavg−𝑦 θ

10. Instantaneous velocity
O
𝑥
𝑦
A
The instantaneous velocity of
particle at point A is given by
v
v =
dr
dt
=
d𝑥 𝑖 + d𝑦 𝑗
dt
v =
d𝑥
dt
𝑖 +
d𝑦
dt
𝑗
v = v 𝑥 𝑖 + v 𝑦 𝑗

11. v = v 𝑥
2 + v 𝑦
2
Magnitude & direction of instantaneous velocity
Magnitude:
v
v 𝑥
v 𝑦
θ
Direction:
θ = tan−1
v 𝑦
v 𝑥
O
𝑥
𝑦
A
v

12. Average acceleration
vA
A
B
∆v
vB
vB
-vA
vA
A
B
∆v
vB
aavg

13. Average acceleration
vA
A
B
vB
O
𝑦
𝑥
The average acceleration of particle
from point A to point B is given by
aavg =
∆v
∆t
=
∆v 𝑥 𝑖 + ∆v 𝑦 𝑗
∆t
aavg =
∆v 𝑥
∆t
𝑖 +
∆v 𝑦
∆t
𝑗
aavg = aavg−𝑥 𝑖 + aavg−𝑦 𝑗
∆v
aavg

14. Magnitude & direction of average acceleration
vA
A
B
vB
O
𝑦
𝑥
aavg
aavg−𝑥
aavg−𝑦
Magnitude:
aavg = aavg−𝑥
2
+ aavg−𝑦
2
Direction:
θ = tan−1
aavg−𝑦
aavg−𝑥
θ

15. Instantaneous acceleration
vA
A
O
𝑦
𝑥
a
The instantaneous acceleration of
particle at point A is
a =
dv
dt
=
dv 𝑥 𝑖 + dv 𝑦 𝑗
dt
a =
dv 𝑥
dt
𝑖 +
dv 𝑦
dt
𝑗
a = a 𝑥 𝑖 + a 𝑦 𝑗

16. Magnitude & direction of instantaneous acceleration
vA
A
O
𝑦
𝑥
a
a 𝑥
a 𝑦
θ
a = a 𝑥
2 + a 𝑦
2
Magnitude:
Direction:
θ = tan−1
a 𝑦
a 𝑥

17. Tangential & normal component of acceleration
a
at
an
at = tangential componet of
acceleration
It changes the speed of particle
an = normal componet of
acceleration
It changes the direction of particle
v
A

18. Tangential & normal component of acceleration
Speed is constant Speed is increasing Speed is decreasing
v
a = an
v
a
at
an
v
a
at
an
A A A

19. Thank
you