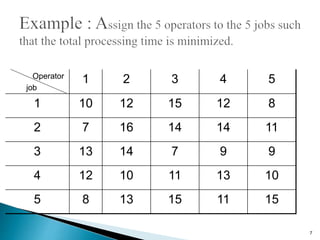
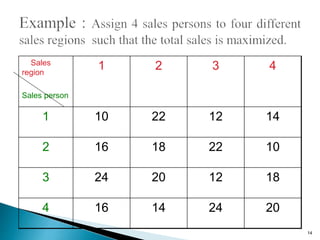
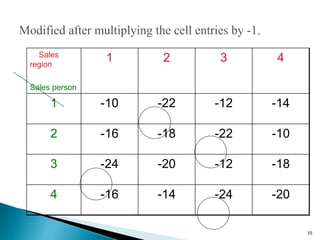
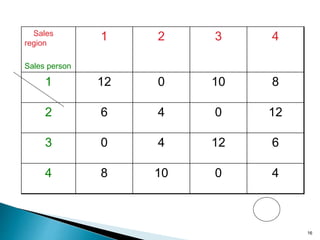
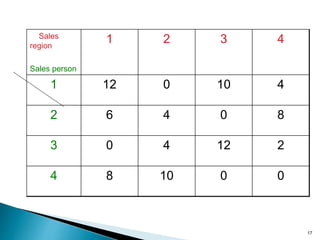
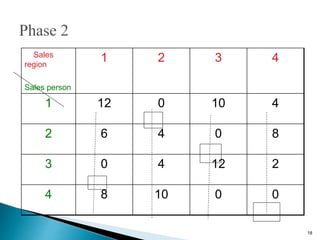
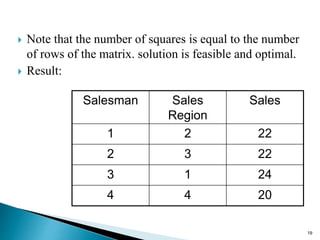
This document discusses the assignment problem and provides an example of how to solve it using the Hungarian method. It begins by defining the assignment problem and providing examples of problems that can be modeled as assignment problems. It then explains how to use the Hungarian method, which involves two phases - first reducing rows and columns to get zeros, then finding the minimum number of lines to cover all zeros. An example of using the Hungarian method on a sales assignment problem is worked through step-by-step to find the optimal assignment.

1. Dr. R K Vidhate
Assistant Professor
GNIT Nagpur

2.  This is a special type of transportation
problem in which each source should have the
capacity to fulfill the demand of any of the
destinations.
2

3. Operators
Job
1 2 … j … m
1 t11 t12 t1j t1m
2
.
i ti1 tij tim
.
m tm1 tm2 tmj tmm
3
General format of assignment problem

4.  Examples of assignment problem
4
Row entity Column entity Cell entity
jobs operators Processing time
Programmer program Processing time
operators machine Processing time
Drivers Routes Travel time
Teachers Subjects Students pass
percentage

5.  Min Z= c11x11++cijXij+.+cmmXmm
=
 Subject to x11+…………...+x1m =1
x21+…………...+x2m =1
……..
xm1+…………...+xmm =1
x11+…………...+xm1 =1
x12+…………...+xm2 =1
………………..
x1m+…………...+xmm =1
xij.=0 or 1 for i=1,2….m and
j=1,2…..m.
m
j
for
X
m
i
for
X
X
C
Z
Min
m
i
ij
m
j
ij
m
i
m
j
ij
ij
,....
1
1
,....
1
1
1
1
1 1










 
5

6.  As in transportation problems assignment
problems also can be balanced ( with equal
number of rows and columns) or unbalanced.
 When it is unbalanced the necessary number of
row/s or column/s are added to balance it. That
is to make a square matrix.
 The values of the cell entries of the dummy rows
or columns will be made equal to zero.
6

7. Operator
job
1 2 3 4 5
1 10 12 15 12 8
2 7 16 14 14 11
3 13 14 7 9 9
4 12 10 11 13 10
5 8 13 15 11 15
7

8.  Consists of two phases.
 First phase: row reductions and column
reductions are carried out.
 Second phase :the solution is optimized in
iterative basis.
8

9.  Step 0: Consider the given cost matrix
 Step 1: Subtract the minimum value of
each row from the entries of that row, to
obtain the next matrix.
 Step 2: Subtract the minimum value of
each column from the entries of that
column , to obtain the next matrix.
 Treat the resulting matrix as the input for
phase 2.
9

10.  Step3: Draw a minimum number of lines to
cover all the zeros of the matrix.
 Procedure for drawing the minimum number
of lines:
 3.1 Row checking
1 Starting from the first row ,if there’s only one
zero in a row mark a square round the zero
entry and draw a vertical line passing through
that zero. Otherwise skip the row.
2.After scanning the last row, check whether all
the zeros are covered with lines. If yes go to
step 4. Otherwise do column scanning. 
10

11.  3.2 Column checking
1. Starting from the first column: if there’s
only one zero in a column mark a square
round the zero entry and draw a horizontal
line passing through that zero. otherwise
skip the column.
2.After scanning the last column, check
whether all the zeros are covered with
lines. If yes go to step 4. Otherwise do row
scanning. 
11

12.  Step 4: check whether the number of squares
marked is equal to the number of
rows/columns of the matrix.
 If yes go to step 7. Otherwise go to step 5.
 Step 5: Identify the minimum value of the
undeleted cell values ,say ‘x’. Obtain the next
matrix by the following steps.
5.1 Copy the entries covered by the lines ,but
not on the intersection points.
5.2 add x to the intersection points
5.3 subtract x from the undeleted cell values.
Step 6: go to step 3.
Step 7: optimal solution is obtained as marked
by the squares
12

13.  If the problem is a maximization problem
,convert the problem into a minimization
problem by multiplying by -1.
 Then apply the usual procedure of an
assignment problem.
13

14. Sales
region
Sales person
1 2 3 4
1 10 22 12 14
2 16 18 22 10
3 24 20 12 18
4 16 14 24 20
14

15. Sales
region
Sales person
1 2 3 4
1 -10 -22 -12 -14
2 -16 -18 -22 -10
3 -24 -20 -12 -18
4 -16 -14 -24 -20
15

16. Sales
region
Sales person
1 2 3 4
1 12 0 10 8
2 6 4 0 12
3 0 4 12 6
4 8 10 0 4
16

17. Sales
region
Sales person
1 2 3 4
1 12 0 10 4
2 6 4 0 8
3 0 4 12 2
4 8 10 0 0
17

18. Sales
region
Sales person
1 2 3 4
1 12 0 10 4
2 6 4 0 8
3 0 4 12 2
4 8 10 0 0
18

19.  Note that the number of squares is equal to the number
of rows of the matrix. solution is feasible and optimal.
 Result:
Salesman Sales
Region
Sales
1 2 22
2 3 22
3 1 24
4 4 20
19