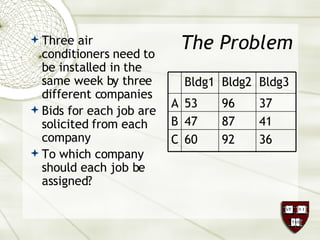
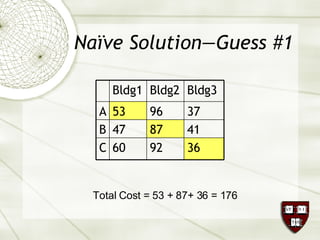
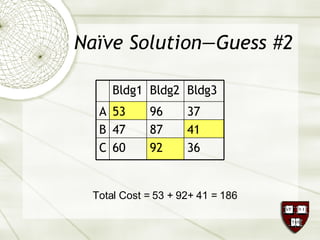
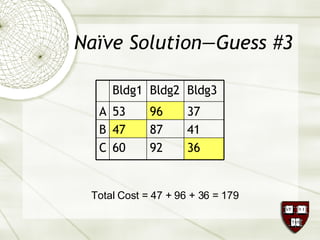
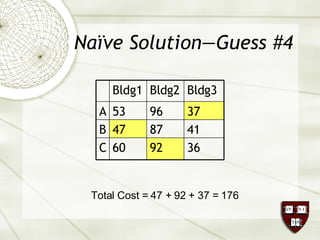
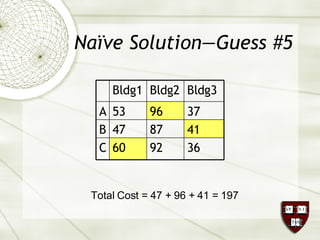
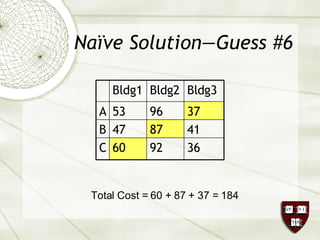
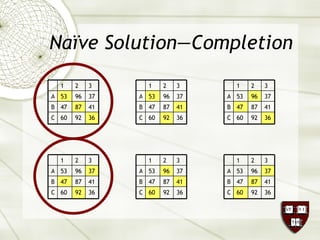
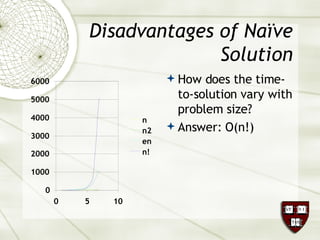
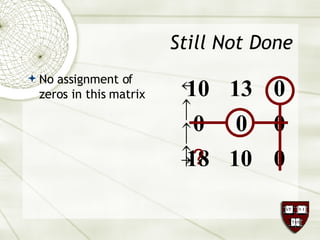
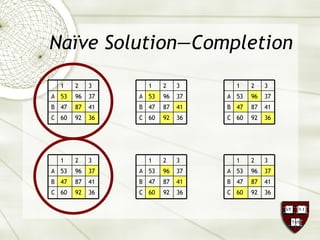
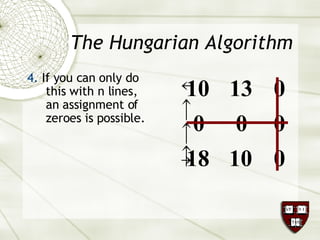
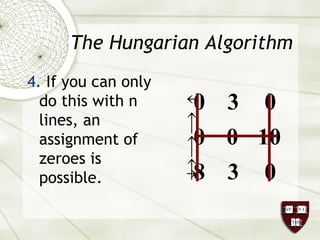
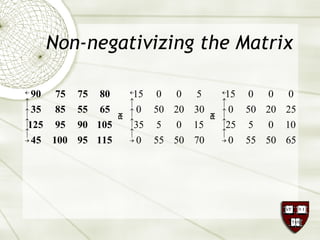
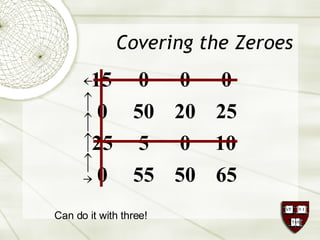
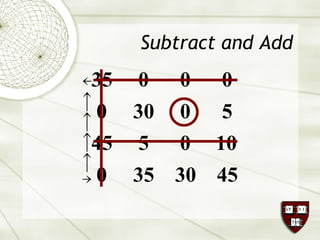
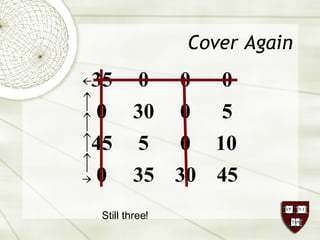
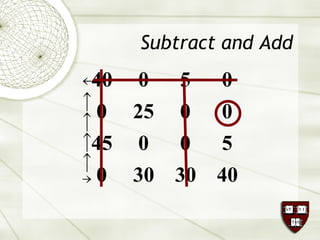
The document discusses the assignment problem in mathematics, highlighting methods to allocate jobs to companies efficiently to minimize costs, particularly through the use of the Hungarian algorithm. It illustrates the naïve solution and its limitations, explaining how to reformulate the cost matrix to find optimal assignments. Additionally, it provides examples of the problem's real-world applications, including air conditioning installation and taxi dispatching.

1. Lesson 31 The Assignment Problem Math 20 Algebra and Multivariable Mathematics for Social Sciences December 10, 2007

2. The Problem Three air conditioners need to be installed in the same week by three different companies Bids for each job are solicited from each company To which company should each job be assigned? 36 92 60 C 41 87 47 B 37 96 53 A Bldg3 Bldg2 Bldg1

3. Na ïve Solution There are only 6 possible assignments of companies to jobs Check them and compare

4. Na ïve Solution—Guess #1 Total Cost = 53 + 87+ 36 = 176 36 92 60 C 41 87 47 B 37 96 53 A Bldg3 Bldg2 Bldg1

5. Na ïve Solution—Guess #2 Total Cost = 53 + 92+ 41 = 186 36 92 60 C 41 87 47 B 37 96 53 A Bldg3 Bldg2 Bldg1

6. Na ïve Solution—Guess #3 Total Cost = 47 + 96 + 36 = 179 36 92 60 C 41 87 47 B 37 96 53 A Bldg3 Bldg2 Bldg1

7. Na ïve Solution—Guess #4 Total Cost = 47 + 92 + 37 = 176 36 92 60 C 41 87 47 B 37 96 53 A Bldg3 Bldg2 Bldg1

8. Na ïve Solution—Guess #5 Total Cost = 47 + 96 + 41 = 197 36 92 60 C 41 87 47 B 37 96 53 A Bldg3 Bldg2 Bldg1

9. Na ïve Solution—Guess #6 Total Cost = 60 + 87 + 37 = 184 36 92 60 C 41 87 47 B 37 96 53 A Bldg3 Bldg2 Bldg1

10. Na ïve Solution—Completion 36 92 60 C 41 87 47 B 37 96 53 A 3 2 1 36 92 60 C 41 87 47 B 37 96 53 A 3 2 1 36 92 60 C 41 87 47 B 37 96 53 A 3 2 1 36 92 60 C 41 87 47 B 37 96 53 A 3 2 1 36 92 60 C 41 87 47 B 37 96 53 A 3 2 1 36 92 60 C 41 87 47 B 37 96 53 A 3 2 1

11. Disadvantages of Na ïve Solution How does the time-to-solution vary with problem size? Answer: O(n!)

12. Rates of Growth

13. Mathematical Modeling of the Problem Given a Cost Matrix C which lists for each “company” i the “cost” of doing “job” j . Solution is a permutation matrix X : all zeros except for one 1 in each row and column Objective is to minimize the total cost

14. An Ideal Cost Matrix All nonnegative entries An possible assignment of zeroes, one in each row and column In this case the minimal cost is apparently zero!

15. The Hungarian Algorithm Find an “ideal” cost matrix that has the same optimal assignment as the given cost matrix From there the solution is easy!

16. Critical Observation Let C be a given cost matrix and consider a new cost matrix C’ that has the same number added to each entry of a single row of C For each assignment, the new total cost differs by that constant The optimal assignment is the same as before

17. Critical Observation Same is true of columns So: we can subtract minimum entry from each row and column to insure nonnegative entries

18. On our given matrix

19. Still Not Done No assignment of zeros in this matrix

20. Still Not Done No assignment of zeros in this matrix

21. Still Not Done No assignment of zeros in this matrix

22. Still Not Done No assignment of zeros in this matrix

23. Still Not Done No assignment of zeros in this matrix ?

24. Still Not Done No assignment of zeros in this matrix Still, we can create new zeroes by subtracting the smallest entry from some rows

25. Still Not Done No assignment of zeros in this matrix Still, we can create new zeroes by subtracting the smallest entry from some rows Now we can preserve nonnegativity by adding that entry to columns which have negative entries

26. Solutions

27. Na ïve Solution—Completion 36 92 60 C 41 87 47 B 37 96 53 A 3 2 1 36 92 60 C 41 87 47 B 37 96 53 A 3 2 1 36 92 60 C 41 87 47 B 37 96 53 A 3 2 1 36 92 60 C 41 87 47 B 37 96 53 A 3 2 1 36 92 60 C 41 87 47 B 37 96 53 A 3 2 1 36 92 60 C 41 87 47 B 37 96 53 A 3 2 1

28. The Hungarian Algorithm Find the minimum entry in each row and subtract it from each row Find the minimum entry in each column and subtract it from each column Resulting matrix is nonnegative

29. The Hungarian Algorithm 3. Using lines that go all the way across or all the way up-and-down, cross out all zeros in the new cost matrix Find a way to do this with a minimum number of lines (≤n)

30. The Hungarian Algorithm 4. If you can only do this with n lines, an assignment of zeroes is possible.

31. The Hungarian Algorithm Otherwise, determine the smallest entry not covered by any line. Subtract this entry from all uncovered entries Add it to all double-covered entries Return to Step 3.

32. The Hungarian Algorithm 3. Using lines that go all the way across or all the way up-and-down, cross out all zeros in the new cost matrix

33. The Hungarian Algorithm 3. Using lines that go all the way across or all the way up-and-down, cross out all zeros in the new cost matrix

34. The Hungarian Algorithm 3. Using lines that go all the way across or all the way up-and-down, cross out all zeros in the new cost matrix

35. The Hungarian Algorithm 4. If you can only do this with n lines, an assignment of zeroes is possible.

36. Solutions

37. Example 2 A cab company gets four calls from four customers simultaneously Four cabs are out in the field at varying distance from each customer Which cab should be sent where to minimize total (or average) waiting time? 11.5 9.5 11.0 4.5 D 10.5 9.0 9.5 12.5 C 6.5 5.5 8.5 3.5 B 8 7.5 7.5 9 A Cab 4 3 2 1 Customer

38. Integerizing the Matrix

39. Non-negativizing the Matrix

40. Covering the Zeroes Can do it with three!

41. Find Smallest Uncovered Entry

42. Subtract and Add

43. Cover Again Still three!

44. Find Smallest Uncovered

45. Subtract and Add

46. Cover Again Done!

47. Solutions Done!

48. Solutions Total Cost = 27.5

49. Other Applications of AP Assigning teaching fellows to time slots Assigning airplanes to flights Assigning project members to tasks Determining positions on a team Assigning brides to grooms (once called the marriage problem )