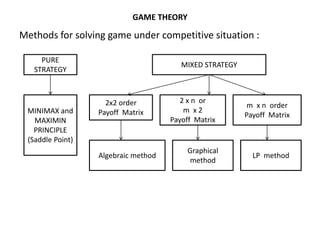
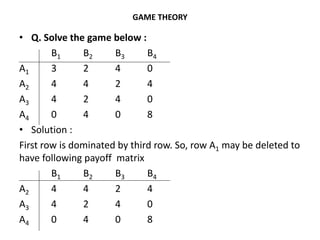
Game theory is used to model strategic decision-making between competitors. It originated in the 20th century and applies concepts like players, strategies, and payoffs. Players select strategies and receive payoffs based on the strategies of all players. The optimal strategy maximizes a player's payoff. Techniques like minimax, maximin, and solving dominance-reduced payoff matrices can help determine optimal strategies and the value of a game.

1. GAME THEORY

2. GAME THEORY
• Game theory came into existence in 20th century.
• In Business and Economics literature, the term ‘Game’ refers
to a competition in which two or more competitors are
involved in the decision making process in anticipation of
certain outcome over a period of time.
• The competitors are referred to as ‘players’. A player may be
an individual, a group of individuals or an organization.
• A few examples of application of game theory in selecting an
optimal strategy are :
1. Pricing of products where the sales of an organization are
determined not only by the price level it selects but also by
the prices its competitors set.
2. Fixing of TV program in a TV channel are mostly determined
depending on what the competitors present in same slot.

3. GAME THEORY
• Strategy : The strategy of a player is the list of all “possible
actions” that he takes for attaining the payoff(outcome)
which results from a particular action. The outcome resulting
from a particular action is known to the players in advance
and is expressed in terms of numerical values.
• Pure strategy : Each player knows in advance all strategies and
only one strategy which is selected by a player to maximize
his gain or minimize his loss regardless of the other player’s
strategy is called pure strategy.
• Mixed Strategy : The course of actions which are selected on
a particular occasion with some fixed probability are called
mixed strategy.
• Optimal Strategy : The particular strategy by which a player
optimizes his gain or loss is called optimal strategy.

4. GAME THEORY
• Value of Game : The expected outcome of the game when
players follow their optimal strategy is called the value of the
game.
• Two-Person-Zero-Sum Games : A game with only two players
say player-A and player-B, is called a two-person-zero-sum
game, if gain of one player is equal to the loss of other player
so that the total sum is zero.
• Payoff matrix : In game theory, the payoffs are quantitative
measure of achievement in terms of gains or loss. The
representation of payoffs of players against their particular
strategies in the form of a matrix is called payoff matrix.

5. GAME THEORY
Methods for solving game under competitive situation :
PURE
STRATEGY
MINIMAX and
MAXIMIN
PRINCIPLE
(Saddle Point)
MIXED STRATEGY
2x2 order
Payoff Matrix
2 x n or
m x 2
Payoff Matrix
m x n order
Payoff Matrix
Algebraic method
Graphical
method
LP method

6. GAME THEORY
MINIMAX and MAXIMIN Principles : Games with Saddle Point
• Maximin Principle : For player-A , the minimum value in each
row represents the least gain(payoff) to him, if he chooses his
particular strategy. These are written in the matrix by row
minima. He will then select the strategy that gives the largest
gain among the row minimum values. This choice of player-A
is called the maximin principle, and the corresponding gain is
called the maximin value of the game.
• Minimax Principle : For player-B, who is assumed to be a
looser, the maximum value in each column represents the
maximum loss to him, if he chooses his particular strategy.
These are written in the payoff matrix by column maxima.He
will then select the strategy that gives the minimum loss
among the column maximum values. This choice of player-B is
called minimax principle, and the corresponding loss is called
the minimax value of the game.

7. GAME THEORY
• Saddle Point : In a game, if the maximin value equals the
minimax value, then the game is said to have a saddle
(equilibrium) point .
• Rules to determine saddle point :
1. Select the minimum element in each row of the payoff
matrix and write them under “Row minima” heading. Then
select the largest element among these elements and
enclose it in a rectangle, .
2. Select the maximum element in each column of the payoff
matrix and write them under “column maxima” heading .
Then select the lowest element among these elements and
enclose it in a circle, .
3. Find out the element(s) that is same in the circle as well as in
the rectangle and mark the position of such element(s) in the
matrix. This element represents the value of the game and is
called the saddle (or equilibrium) point.

8. GAME THEORY
Example 1. For the game with payoff matrix :
Player B
Player A B1 B2 B3
A1 -1 2 -2
A2 6 4 -6
Solution :
Player B
Player A B1 B2 B3 Row minimum
A1 -1 2 Maximin
A2 6 4 -6 -6
Column Max. 6 4 Minimax
Here saddle point is -2. Therefore, value of the game, V = -2
-2 -2
-2

9. GAME THEORY
• Q. A company management and the labour union are
negotiating a new 3 years settlement. Each of these has 4
strategies as shown below. What is the value of the game?
I : Hard and aggressive bargaining
II: Reasoning and logical approach
III: Legalistic strategy
IV: Conciliatory approach
Company strategies
Union strategies I II III IV
I 20 15 12 35
II 25 14 8 10
III 40 2 10 5
IV -5 4 11 0

10. GAME THEORY
The rules of Dominance :
• The rules of Dominance are used to reduce the size of the
Payoff matrix
• The rules of Dominance are used for evaluation of 2-person
zero-sum game.
1. For player-B, who is assumed to be a looser, if each element
in a column, say Cr is greater than or equal to corresponding
element in another column, say Cs in the payoff matrix, then
column Cr is said to be dominated by column Cs, then column
Cr can be deleted from the payoff matrix . Player-B will never
use the strategy that corresponds to column Cr because he
will loose more by choosing such strategy.

11. GAME THEORY
2. For player-A, who is assumed to be gainer, if each element
in a row, say Rr, is less than or equal to the corresponding
element in another row, say Rs, in the payoff matrix, then the
row Rr is said to be dominated by row Rs, then the row Rr can be
deleted from the payoff matrix. Player-A will never use the
strategy corresponding to row Rr because he will gain less by
choosing such a strategy.
3. A strategy say K can also be dominated, if it is inferior(less
attractive) to an average of two or more other pure strategies. In
this case, if domination is strict, K can be deleted. If, strategy
dominates the convex linear combination of some other pure
strategies, then one of the pure strategies involved in the
combination may be deleted.

12. GAME THEORY
PLAYER-B
PLAYER-A B1 B2 B3
A1 a11 a12 a13 Row Rr
A2 a21 a22 a23 Ror Rs
A3 a31 a32 a33
Column : Cr Cs

13. GAME THEORY
• For solving a 2 x 2 Game, without saddle point, the following
formula is used, if payoff matrix for player-A is given by :
Player-B
B1 B2
Player-A (Prob. q1) (prob. q2 )
A1 (Probability p1 ) a11 a12
A2 (Probability p2 ) a21 a22
• Then following formulae are used to find the value of Game
and optimal strategies :
• p1 = [ a22 – a21] / [(a11 + a22) – (a12 + a21)] ; p2 = 1 – p1
• q1 = [ a22 – a12] / [(a11 + a22) – (a12 + a21)] ; q2 = 1 – q1
• V = [a11 a22 – a21 a12] / [(a11 + a22) – (a12 + a21)]

14. GAME THEORY
Q. Find the optimal strategies for Player A and B in the following
game. Also obtain the value of the game.
• Player-B
Player-A B1 B2 B3
A1 9 8 -7
A2 3 -6 4
A3 6 7 -7
• Player-A B1 B2 B3
A1 9 8 -7
A2 3 -6 4

15. GAME THEORY
Player-B
• Player-A B2 B3
A1 : P1 8 -7
A2 : P2 - 6 4
q1 q2
• p1 = [ a22 – a21] / [(a11 + a22) – (a12 + a21)]
• = [4 –(-6)] / [(8 +4) – {(-7) + (-6)}] = 10/(12 + 13) = 10/25 = 2/5
• P2 = 1 – p1 = 1- 2/5 = 3/5
• q1 = [ a22 – a12] / [(a11 + a22) – (a12 + a21)]
• = [4 – (-7)] / [(8 +4) – {(-7) + (-6)}] = 11/(12 + 13) = 11/25
• q2 = 1 – q1 = 1 – 11/25 = 14/25
• Value of game, V = [a11 a22 – a21 a12] / [(a11 + a22) – (a12 + a21)]
• = [8 x 4 – (-6) x (-7)] / [(8 +4) – {(-7) + (-6)}]
• = [32 – 42] / [12 + 13] = -10/25 = - 2/5

16. GAME THEORY
• Q. Solve the game below :
B1 B2 B3 B4
A1 3 2 4 0
A2 4 4 2 4
A3 4 2 4 0
A4 0 4 0 8
• Solution :
First row is dominated by third row. So, row A1 may be deleted to
have following payoff matrix
B1 B2 B3 B4
A2 4 4 2 4
A3 4 2 4 0
A4 0 4 0 8

17. GAME THEORY
• In the reduced 3 x 4 matrix above, first column is dominated
by third column. So, B1 may be deleted to get the following
3 x 3 matrix.
B2 B3 B4
A2 4 2 4
A3 2 4 0
A4 4 0 8
• In the above matrix, average of payoff due to strategy B3, B4
{(2+4)/2; (4+0)/2; (0+8)/2} is superior to payoff due to strategy
strategy B2 of player B. Thus, B2 may be deleted and new
payoff table is shown below :

18. GAME THEORY
• B3 B4
A2 2 4
A3 4 0
A4 0 8
• The average of payoff due to strategies A3 and A4 of player-A
i.e. {(4+0)/2; (0+8)/2} is same as the payoff due to strategy A2.
Therefore, player-A will gain same amount even if the strategy, A2
is never used. Hence after deleting strategy A2 from the above
reduced matrix, the following new reduced 2 x 2 payoff matrix is
obtained :
• B3 B4
Probability, P1 A3 4 0
Probability, P2 A4 0 8
q1 q2 Probability of playing strategy
by player-B

19. GAME THEORY
• Since, both players want to retain their interest unchanged,
therefore,
• 4.p1 + 0.p2 = 0.p1 + 8.p2 and 4.q1 + 0.q2 = 0.q1 + 8.q2
• or, 4p1 = 8p2 ………..(1) or, 4q1 = 8q2 …………..(2)
• We have also, p1 + p2 = 1 ……(3) and q1 + q2 = 1……………..(4)
• Solving Equations (1) & (3) and (2) & (4) we get,
• P1 = 2/3, p2=1/3 and q1=2/3, q2=1/3
• The optimal strategies of Player-A and Player-B in the original
Game are :
• (0, 0, 2/3, 1/3) and (0, 0, 2/3, 1/3)
• Expected gain to Player-A = 4.p1 + 0.p2 = 4 x 2/3 = 8/3
• Expected loss to Player-B = 4.q1 + 0.q2 = 4 x 2/3 = 8/3
• Value of the game = [4x8 + 0x0]/[(4+8) – (0 + 0)]=8/3

20. GAME THEORY
Q. Players A and B play a game in which each has
three coins, a 5p, 10p and 20p. Each selects a coin
without the knowledge of the other’s choice. If
the sum of the coins is an odd amount, then A
wins B’s coin. But, if sum is even, then B wins A’s
coin. Find the best strategy for each player and the
value of the game.

21. GAME THEORY
PLAYER – B
PLAYER-A B1 (5p) B2 (10p) B3 (15p)
A1 (5p) ……. ……… ……….
A2 (10p) ……. ………. ……..
A3 (15p) ……. ………. ……….

22. GAME THEORY
Solution :
PLAYER – B
PLAYER-A B1 B2 B3
A1 -5 10 20
A2 5 -10 -10
A3 5 -20 -20
PLAYER-B
PLAYER-A B1 B2
A1 -5 10
A2 5 -10
A3 5 -20

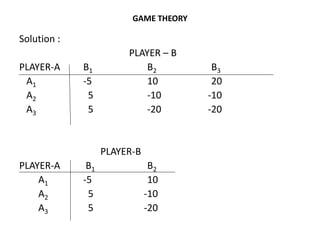
23. GAME THEORY
PLAYER-B
PLAYER-A B1 B2
A1 -5 10 p1 (probability of choosing A1)
A2 5 -10 p2 (Probability of choosing A2)
q1 q2
-5p1 + 5p2 = 10p1 – 10p2 -5q1 + 10q2 = 5q1 -10q2
or, -p1 + p2 = 2p1 – 2p2 or, -10q1 = - 20q2
or, -3p1 = -3p2 or, q1 = 2q2
or, p1 = p2 q1 + q2 = 1
p1 + p2 =1 Therefore, q2 =1/3
Therefore, p1 = 0.5 & p2 =0.5 q1 = 2/3
Value of the game = [a11 a22 – a21 a12] / [(a11 + a22) – (a12 + a21)]
= [(-5).(-10) – (5).(10)] / [{-5+(-10)} – {10 +5}] = 0

24. GAME THEORY
• Q. Solve the following 2 x 5 game graphically :
Player-B
Player-A B1 B2 B3 B4
p1 : A1 8 5 -7 9
p2 : A2 - 6 6 4 -2
• Solution :Let the probability of player-A playing strategy A1 and A2 are p1
and p2 , where p2 = 1 – p1 . Then expected payoff to player-A will be :
• B’s pure strategy A’s expected payoff
B1 8p1 – 6p2
B2 5p1 + 6p2
B3 -7p1 + 4p2
B4 9p1 - 2p2

25. GAME THEORY
6 6
5 5
4 4
3 3
2 2
1 1
0 0
-1 -1
-2 -2
-3 -3
-4 -4
-5 -5
-6 -6

26. 9 9
8 8
7 B4 B1 7
6 B2 6
5 5
4 4
3 3
2 2
1 1
0 0
P2 -1 -1 p1
-2 -2
-3 B3 -3
-4 -4
-5 -5
-6 LOWER ENVELOPE -6
-7 -7
-8 -8
-9 -9

27. GAME THEORY
Player-B
Player-A B1 B3
p1 : A1 8 -7
p2 : A2 - 6 4
q1 q2
• p1 = [ a22 – a21] / [(a11 + a22) – (a12 + a21)]
• = [4 – (-6) ] / [(8 + 4) – {(-7) + (-6)}]
• = [10]/[12 + 13]= 10/25 = 2/5
• P2 = 1 – p1 = 1 – 2/5 = 3/5
• q1 = [ a22 – a12] / [(a11 + a22) – (a12 + a21)]
• = [4 – (-7)] / [(8 +4) – {(-7) + (-6)}] = 11/(12 + 13) = 11/25
• q2 = 1 – q1 = 1 – 11/25 = 14/25
• Value of game, V = [a11 a22 – a21 a12] / [(a11 + a22) – (a12 + a21)]
• = [8 x 4 – (-6) x (-7)] / [(8 +4) – {(-7) + (-6)}]
• = [32 – 42] / [12 + 13] = -10/25 = - 2/5

28. GAME THEORY
• Q. Solve the following 2 x 5 game graphically :
Player-B
Player-A B1 B2 B3 B4 B5
p1 : A1 2 -1 5 -2 6
p2 : A2 -2 4 -3 1 0
• Solution :Let the probability of player-A playing strategy A1 and
A2 are p1 and p2 , where p2 = 1 – p1 . Then expected payoff to
player-A will be :
• B’s pure strategy A’s expected payoff
B1 2p1 – 2p2
B2 -1p1 + 4p2
B3 5p1 - 3p2
B4 -2p1 + 1p2
B5 6p1 + 0.p2

29. GAME THEORY
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
0 P2 0 P1
-1 -1
-2 -2
-3 -3
-4 -4
-5 -5
-6 -6
-7 -7

30. GAME THEORY
• Next the expected payoff for all the strategies of Player-B has been drawn in Fig.1.
The highest point on the lower boundary of these lines will give maximum expected
payoff among the minimum expected payoffs on lower boundary and the optimum
values of probability p1 and p2.
• 6 6
• 5 5
• 4 4
• 3 3
• 2 2
• 1 1
• 0 0
• -1 B1 B4 -1
• -2 -2
• -3 We consider Maximin point -3
-4 since player-A wants to maximise his gain -4
• -5 LOWER ENVELOPE -5
P2 p1

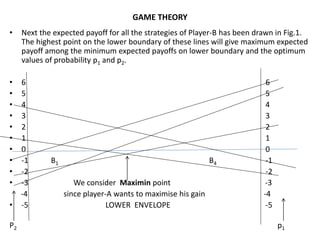
31. GAME THEORY
• The Maximin point shows that the reduced payoff matrix for player-A is :
Player-B
Player-A B1 B4
A1 2 -2
A2 -2 1
• Let SA = A1 A2 be the mixed strategies for player-A
p1 p2
• Then, p1 = [ a22 – a21] / [(a11 + a22) – (a12 + a21)]
• = [ 1 – (-2)] / [ (2+1) – (-2 -2)] = 3/7
• p2 = 1 – p1 = 1 – 3/7 = 4/7
• q1 = [ a22 – a12] / [(a11 + a22) – (a12 + a21)]
• = [1 – (-2)] / [(2+1) – (-2-2)] = 3/7
• q2 = 1 – q1 = 1 – 3/7 = 4/7
• Value of Game, V = [a11 a22 – a21 a12] / [(a11 + a22) – (a12 + a21)]
• =[(2)x(1) - (-2)x(-2)] / [(2+1) – (-2 – 2)]
• = - 2/7

32. GAME THEORY
Q. Obtain the optimal strategies for both the players and the value of the
game whose payoff matrix is as follows :
Player-B
Player-A B1 B2
A1 1 -3
A2 3 5
A3 -1 6
A4 4 -1
A5 2 2
A6 -5 0
• Solution : The given problem does not possess any saddle point. So, the
Player-B plays his mixed strategy, SB = B1 B2 with q2 = 1 – q1 against
q1 q2
Player-A. Then B’s expected payoff against player-A’s pure moves are given by
: Player A’s pure move Player-B’s expected payoff
A1 1q1 – 3q2

33. • Player A’s pure move Player-B’s expected payoff
A2 3q1 + 5q2
A3 -1q1 + 6q2
A4 4q1 - 1q2
A5 2q1 + 2q2
A6 -5q1 + 0.q2
• The expected payoff equations are then plotted as functions of q1 in
graph.
• The given payoff matrix is now reduced to (see the graph) :
B1 B2
P1 A2 3 5
P2 A4 4 -1
q1 q2
Probability

34. GAME THEORY
• 6 6
• 5 A2 5
• 4 4
• 3 A4 3
• 2 2
• 1 1
• 0 0
• -1 -1
• -2 -2
• -3 -3
• -4 -4
• -5 -5
• -6 -6
q2 q1

35. GAME THEORY
• p1 = [ a22 – a21] / [(a11 + a22) – (a12 + a21)]
• = [ -1 -4] / [{3 +(-1)} – {(5 + 4}] = 5/7
• Therefore, p2 = 1 – p1 = 1 – 5/7 = 2/7
• q1 = [ a22 – a12] / [(a11 + a22) – (a12 + a21)]
• = [-1 – 5] / [{3 +(-1)} – {(5 + 4}] = 6/7
• Therefore, q2 = 1 – 6/7 = 1/7
• Value of Game, V = [a11 a22 – a21 a12] / [(a11 + a22) – (a12 + a21)]
• = [ 3 x (-1) – 5x4] / [{3 +(-1)} – {5 + 4}]
• = -23/-7 = 23/7