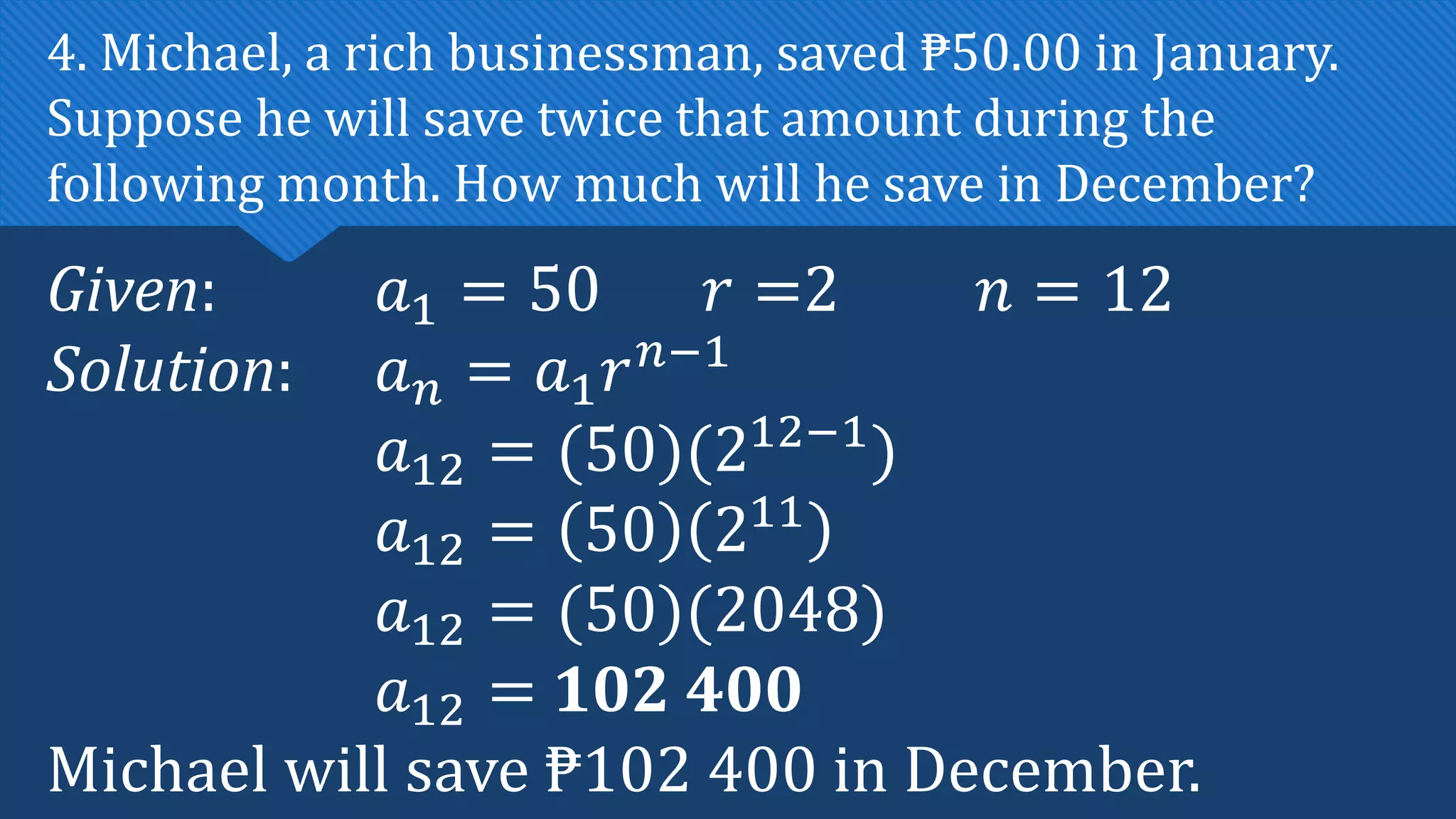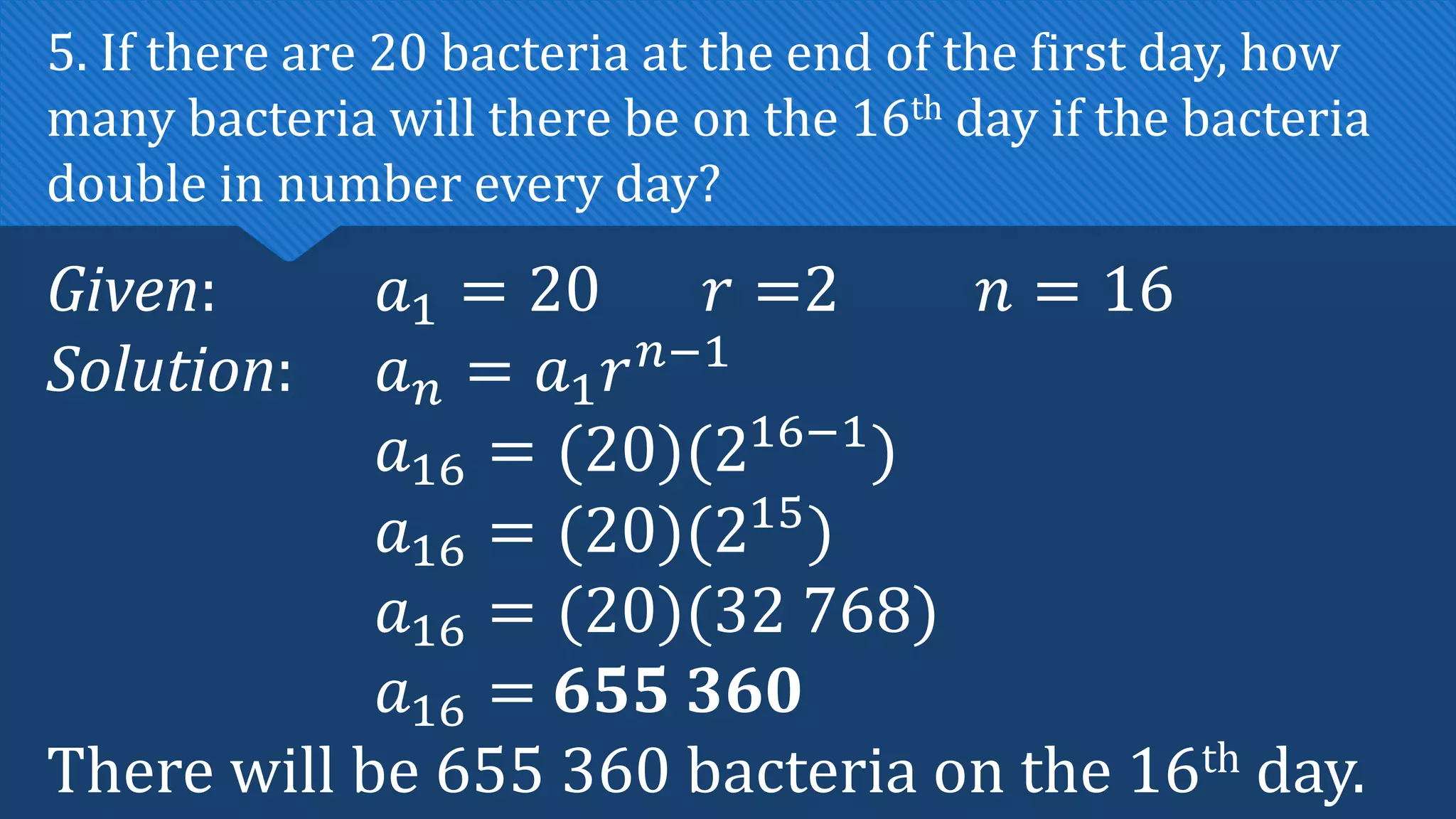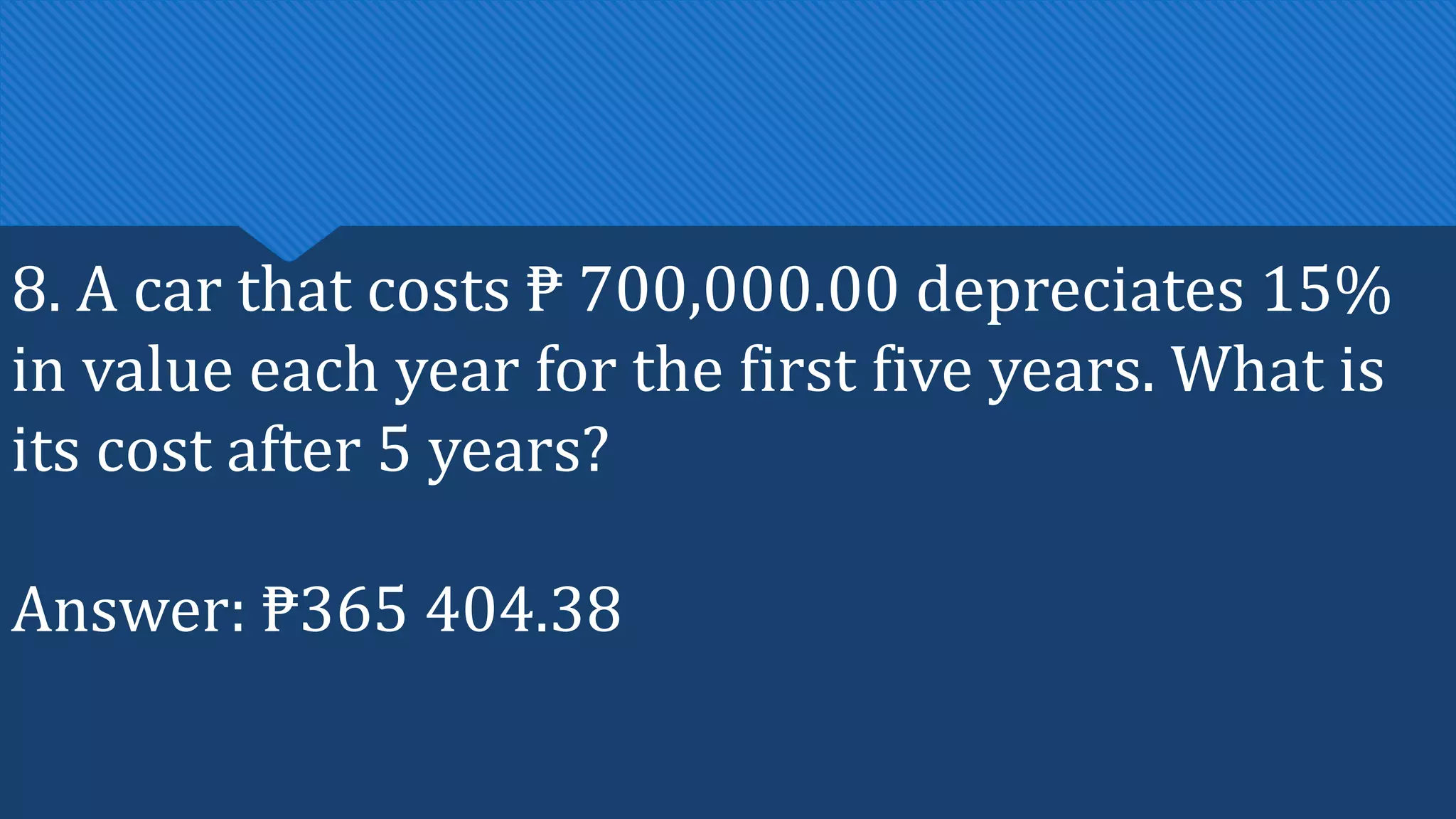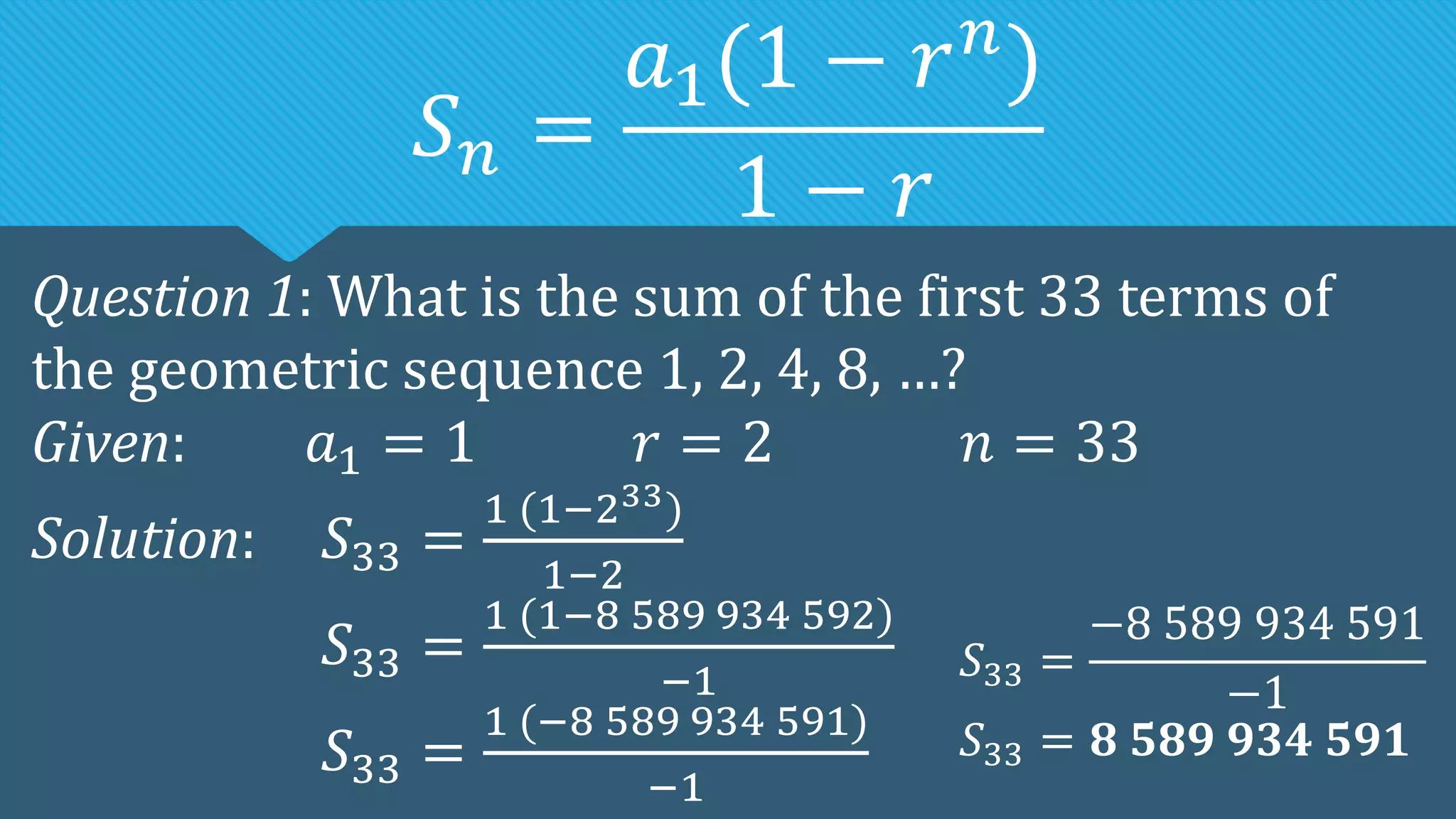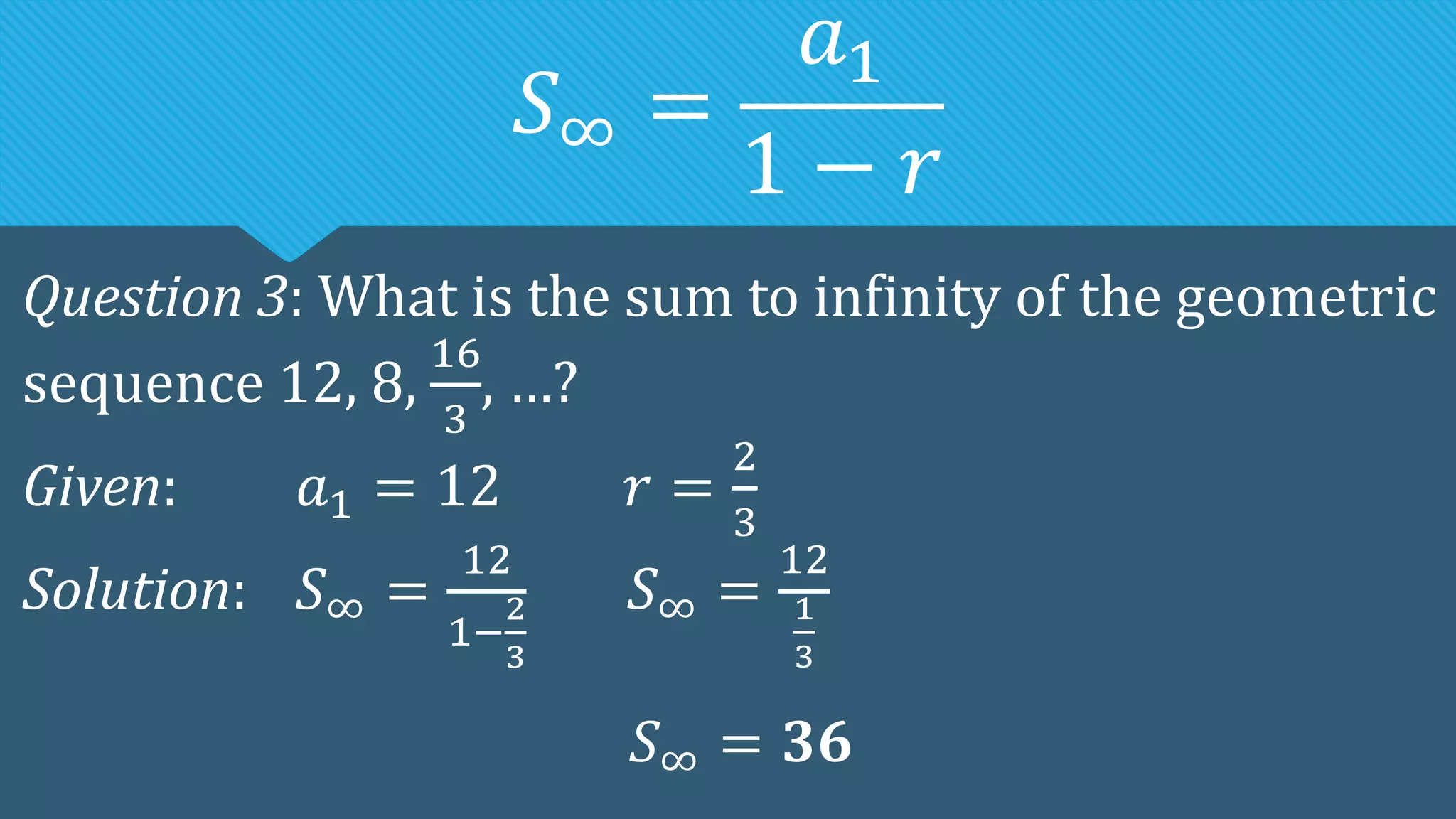The document discusses geometric sequences and series. It defines a geometric sequence as a sequence where each term is obtained by multiplying the preceding term by a constant called the common ratio. It provides examples and discusses how to find the nth term, determine if a sequence is geometric, and calculate the geometric mean. It then introduces geometric series as the sum of the first n terms of a geometric sequence and provides the formulas to calculate finite and infinite geometric series.

2. 1. 2, 6, 18, 54, …
2. 40, 20, 10, 5, …
What can you say about these sequences?

3. Geometric Sequence
• a sequence in which each term is obtained
by multiplying the preceding term by a
constant
The constant is called a common ratio, denoted
as 𝒓.

4. Examples of
Geometric Sequence
1. 2, 6, 18, 54, … 𝑟 = 3
2. 40, 20, 10, 5, … 𝑟 =
1
2
3. 3, -6, 12, -24, … 𝑟 = −2
4.
1
3
,
2
9
,
4
27
,
8
81
, … 𝑟 =
2
3
5.
1
4
, −
3
20
,
9
100
, −
27
500
, … 𝑟 = −
3
5

5. Geometric Sequence or Not?
1. 11, 14, 17, 20, …
2. 4, 8, 16, 32, …
3. 5, 8, 12, 17, 26, …
4. 32, 28, 24, 20, …
5. 1, 8, 27, 64, …

6. Geometric Sequence or Not?
6. 5, 10, 15, 22, 31, …
7. 1, -3, 5, -7, …
8. 4, 12, 36, 108, …
9. 20, 30, 36, 42, …
10.100, -50, 25, −
25
2
, …

7. Finding the Geometric Mean of
Two Numbers
1. 8 and 32 8, ___, 32
2. 4 and 49 4, ___, 49
3. -5 and -180 -5, ___, -180
4.
3
4
and
12
25
3
4
, ___,
12
25
5. 28 and
7
4
28, ___,
7
4

8. Finding the 𝑛th Term of a
Geometric Sequence
Question: What is 𝑎5 in the geometric sequence 2,
6, 18, 54, …?
Answer: It is 162. Multiply 54 by 3 since 𝑟 = 3.
How about finding the 𝑎21?

9. Finding the 𝑛th Term of a
Geometric Sequence
𝑎𝑛 = 𝑎1𝑟𝑛−1
where:
𝑎𝑛 is the 𝑛th term
𝑎1 is the first term
𝑛 is the number of terms
𝑟 is the common ratio

10. Question 1: What is 𝑎21 in the geometric
sequence 2, 6, 18, 54, …?
Given: 𝑎1 = 2 𝑟 = 3 𝑛 = 21
Solution: 𝑎21 = (2)(321−1
)
𝑎21 = (2)(320
)
𝑎21 = (2)(3 486 784 401)
𝑎21 = 𝟔 𝟗𝟕𝟑 𝟓𝟔𝟖 𝟖𝟎𝟐
𝑎𝑛 = 𝑎1𝑟𝑛−1

11. Question 2: In the geometric sequence 6, 12, 24,
48,… , what is 𝑎17?
Given: 𝑎1 = 6 𝑟 = 2 𝑛 = 17
Solution: 𝑎17 = (6)(217−1
)
𝑎17 = (6)(216
)
𝑎17 = (6)(65 536)
𝑎17 = 𝟑𝟗𝟑 𝟐𝟏𝟔
𝑎𝑛 = 𝑎1𝑟𝑛−1

12. Question 3: In a geometric sequence, if the first
term is 2 and the third term is 50, what is the
twelfth term?
Given: 𝑎1 = 2 𝑎3 = 50 𝑟 = 5 𝑛 = 12
Solution: 𝑎12 = (2)(512−1
)
𝑎12 = (2)(511
)
𝑎12 = 𝟗𝟕 𝟔𝟓𝟔 𝟐𝟓𝟎
𝑎𝑛 = 𝑎1𝑟𝑛−1

13. Given: 𝑎1 = 50 𝑟 =2 𝑛 = 12
Solution: 𝑎𝑛 = 𝑎1𝑟𝑛−1
𝑎12 = (50)(212−1
)
𝑎12 = 50 211
𝑎12 = (50)(2048)
𝑎12 = 102 400
Michael will save ₱102 400 in December.
4. Michael, a rich businessman, saved ₱50.00 in January.
Suppose he will save twice that amount during the
following month. How much will he save in December?

14. Given: 𝑎1 = 20 𝑟 =2 𝑛 = 16
Solution: 𝑎𝑛 = 𝑎1𝑟𝑛−1
𝑎16 = (20)(216−1
)
𝑎16 = (20)(215
)
𝑎16 = (20)(32 768)
𝑎16 = 655 360
There will be 655 360 bacteria on the 16th day.
5. If there are 20 bacteria at the end of the first day, how
many bacteria will there be on the 16th day if the bacteria
double in number every day?

15. Given: 𝑎1 = 10 𝑟 =
1
2
𝑛 = 8
Solution: 𝑎𝑛 = 𝑎1𝑟𝑛−1
𝑎8 = (10)
1
2
8−1
𝑎8 = 0.078125 or
𝟓
𝟔𝟒
There will be 0.08 bacteria on the 16th day.
6. A certain radioactive substance decays half of itself
every day. Initially, there are 10 grams. How much
substance will be left after 8 days?

16. “increases by 20%”
(1.00 + 0.20) 𝑟 = 1.20
“decreases / depreciates by 30%”
(1.00 − 0.30) 𝑟 = 0.70
“the next is 40% of the previous” 𝑟 = 0.40
“the next is
1
8
of the previous” 𝑟 =
1
8

17. Given: 𝑎1 = 200 000 𝑟 = 1.1 𝑛 = 5
Solution: 𝑎𝑛 = 𝑎1𝑟𝑛−1
𝑎5 = (200 000)(1.15−1
)
𝑎5 = (200 000)(1.14
)
𝑎5 = (200 000)(1.4641)
𝑎5 = 292 820
The population of the province will be 292 820.
7. The population of a certain province increases by 10%
each year. What will be the population of the province
five years from now if the current population is 200,000?

18. 8. A car that costs ₱ 700,000.00 depreciates 15%
in value each year for the first five years. What is
its cost after 5 years?
Answer: ₱365 404.38

19. 9. Mike deposited ₱850 into the bank in July. From
July to December, the amount of money which he
deposited into the bank increased by 25% per
month. What is the total amount of money in his
account after December?
Answer: ₱2 593.99

20. 10. A radio station has a daily contest in which a random
listener is asked a trivia question. On the first day, the station
gives ₱1000 to the first listener who answers correctly. On
each successive day, the winner takes 90% of the winnings
from the previous day. What is the amount of prize money the
radio station gives away to the 12th listener?
Answer: ₱313.81

21. 11. A radio station has a daily contest in which a random
listener is asked a trivia question. On the first day, the station
gives ₱2500 to the first listener who answers correctly. On
each successive day, the winner takes
4
5
of the winnings from
the previous day. What is the amount of prize money the
radio station gives away to the 9th listener?
Answer: ₱419.43

22. GEOMETRIC SERIES

23. • is the sum of the first 𝑛 terms of a geometric
sequence
• denoted as 𝑺𝒏
Example: What is the sum of the first 5 terms of
the geometric sequence 3, 12, 48, 192, …?
𝑺𝟓 = 𝟑 + 𝟏𝟐 + 𝟒𝟖 + 𝟏𝟗𝟐 + 𝟕𝟔𝟖
𝑺𝟓 = 𝟏 𝟎𝟐𝟑
Finite Geometric Series
(Finding the Sum of the First 𝑛 Terms of a
Geometric Sequence)

24. Finite Geometric Series
How about finding the sum of the first 33 terms
of the geometric sequence 1, 2, 4, 8, …?
𝑺𝟑𝟑 = 𝟏 + 𝟐 + 𝟒 + 𝟖 + ⋯ + 𝒂𝟑𝟑
𝑺𝟑𝟑 =?
(Finding the Sum of the First 𝑛 Terms of a
Geometric Sequence)

25. Finding the Sum of the First 𝑛 Terms
of a Geometric Sequence
𝑆𝑛 =
𝑎1(1 − 𝑟𝑛
)
1 − 𝑟
where: 𝑆𝑛 is the sum of the first 𝑛 terms
𝑎1 is the first term
𝑛 is the number of terms
𝑟 is the common ratio

26. 𝑆𝑛 =
𝑎1(1 − 𝑟𝑛
)
1 − 𝑟
Question 1: What is the sum of the first 33 terms of
the geometric sequence 1, 2, 4, 8, …?
Given: 𝑎1 = 1 𝑟 = 2 𝑛 = 33
Solution: 𝑆33 =
1 (1−233)
1−2
𝑆33 =
1 (1−8 589 934 592)
−1
𝑆33 =
1 (−8 589 934 591)
−1
𝑆33 =
−8 589 934 591
−1
𝑆33 = 𝟖 𝟓𝟖𝟗 𝟗𝟑𝟒 𝟓𝟗𝟏

27. 𝑆𝑛 =
𝑎1(1 − 𝑟𝑛
)
1 − 𝑟
Question 2: What is the sum of the first seven terms
of the geometric sequence -5, 10, -20, 40, …?
Given: 𝑎1 = −5 𝑟 = −2 𝑛 = 7
Solution: 𝑆7 =
−5 (1−(−2)7)
1−(−2)
𝑆7 =
−5(1−(−128))
3
𝑆7 =
−5(129)
3
𝑆7 =
−645
3
𝑆7 = −215

28. 𝑆𝑛 =
𝑎1(1 − 𝑟𝑛
)
1 − 𝑟
Question 3: What is 𝑆6 in the geometric sequence 2,
-8, 32, -128, …?
Given: 𝑎1 = 2 𝑟 = −4 𝑛 = 6
Solution: 𝑆6 =
2 (1−(−4)6)
1−(−4)
𝑆6 =
2 (1−(4 096))
5
𝑆6 =
2 (−4 095)
5
𝑆6 =
−8 190
5
𝑆6 = −1 638

29. Given: 𝑎1 = 1 𝑟 = 2 𝑛 =10
Solution: 𝑆𝑛 =
𝑎1(1−𝑟𝑛)
1−𝑟
𝑆10 =
1 (1−210)
1−2
𝑆10 =
1 (1−1024)
−1
𝑆10 =
1 (−1 023)
−1
.
This October, suppose you save ₱ 1 on the first day, ₱ 2 on the
second day, ₱ 4 on the third day, and so on. Each succeeding day,
you save twice as much as you did the day before. How much will
you save in October 10 all in all?
𝑆10 =
−1 023
−1
𝑆10 = 1 023
You will save ₱ 1 023.

30. Infinite Geometric Series
How about finding the sum of the terms of the
infinite geometric sequence
1
2
,
1
4
,
1
8
,
1
16
…?
𝑺∞ =
1
2
+
1
4
+
1
8
+
1
16
+ ⋯ + 𝑎∞
𝑺∞ =?
(Finding the Sum to Infinity)

31. Finding the Sum to Infinity
𝑆∞ =
𝑎1
1 − 𝑟
where: 𝑆∞ is the sum to infinity
𝑎1 is the first term
𝑟 is the common ratio
Note: Sum to infinity is applied if −𝟏 < 𝒓 < 𝟏.

32. 𝑆∞ =
𝑎1
1 − 𝑟
Question 1: What is the sum of the terms of the
infinite geometric sequence
1
2
,
1
4
,
1
8
,
1
16
…?
Given: 𝑎1 =
1
2
𝑟 =
1
2
Solution: 𝑆∞ =
1
2
1−
1
2
𝑆∞ =
1
2
1
2
𝑆∞ = 1

33. 𝑆∞ =
𝑎1
1 − 𝑟
Question 2: What is the sum of the terms of the
infinite geometric sequence
2
3
,
1
2
,
3
8
,
9
32
…?
Given: 𝑎1 =
2
3
𝑟 =
3
4
Solution: 𝑆∞ =
2
3
1−
3
4
𝑆∞ =
2
3
1
4
𝑆∞ =
𝟖
𝟑

34. 𝑆∞ =
𝑎1
1 − 𝑟
Question 3: What is the sum to infinity of the geometric
sequence 12, 8,
16
3
, …?
Given: 𝑎1 = 12 𝑟 =
2
3
Solution: 𝑆∞ =
12
1−
2
3
𝑆∞ =
12
1
3
𝑆∞ = 𝟑𝟔

35. 𝑆∞ =
𝑎1
1 − 𝑟
Question 4: In a race competition, the prizes are awarded according to the
following rule: the first prize is ₱5000, the second prize is
3
4
of the first prize,
the third prize is
3
4
of the second prize, and so on. How much money do the
organizers need to have for the prize fund assuming that there are no ties?
Given: 𝑎1 = 5000 𝑟 =
3
4
Solution: 𝑆∞ =
5000
1−
3
4
𝑆∞ =
5000
1
4
𝑆∞ = 20000