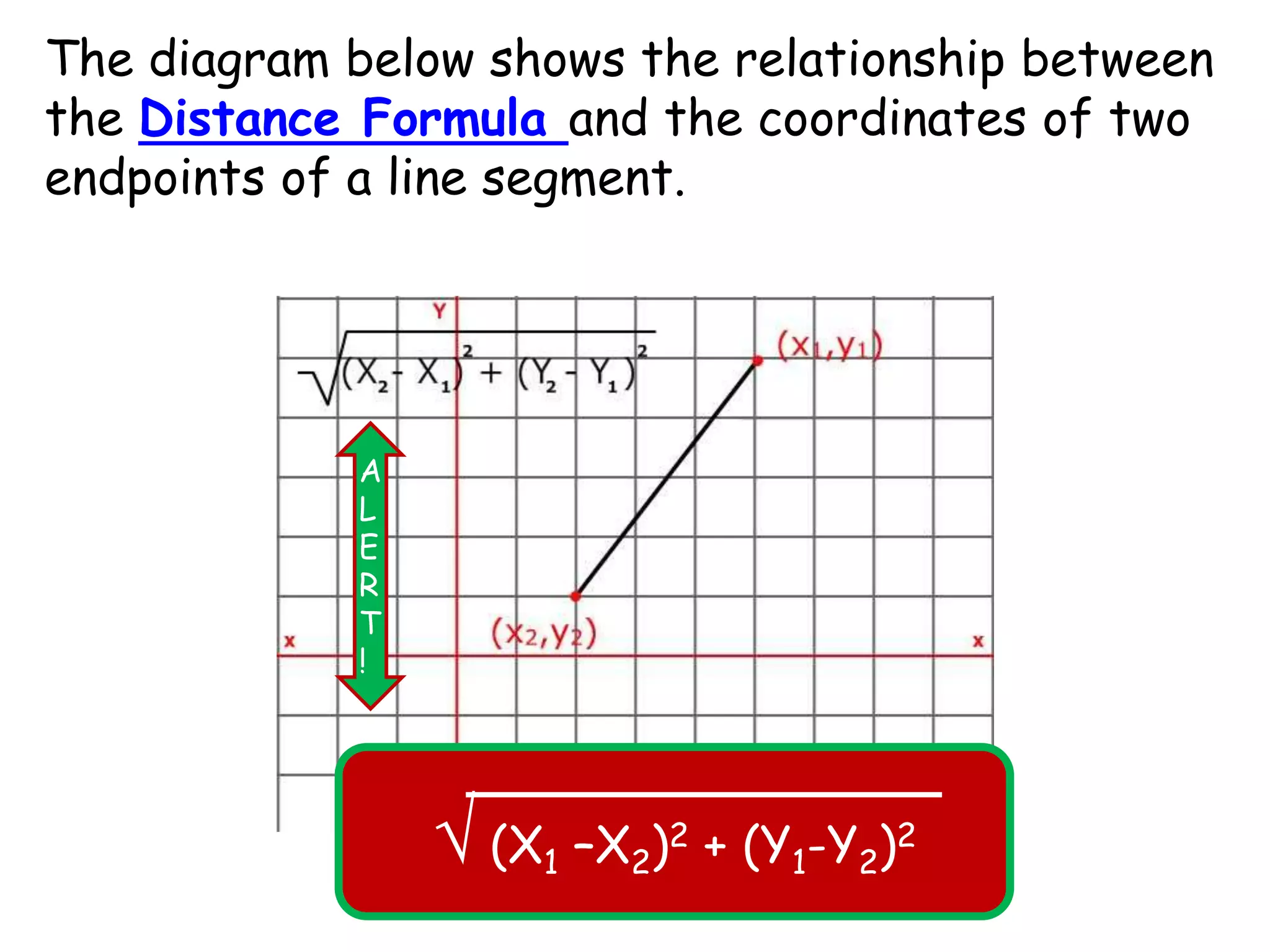
This document introduces the distance formula, which is used to calculate the distance between two points (x1, y1) and (x2, y2) on a coordinate plane. The distance formula is the square root of (x1 - x2) squared plus (y1 - y2) squared. Several examples are worked through to demonstrate finding the distance between points using their coordinates. Practice problems are also provided for the reader to work through on their own.

1. THE DISTANCE FORMULA
During this lesson, we will use the
Distance Formula to measure
distances on the coordinate plane.

2. DISTANCE FORMULA
THE DISTANCE FORMULA
Given the two points (x1, y1) and (x2, y2), the
distance between these points is given by the
formula:
Recall: You pick
which point is
 first, then
(X1 –X2)2 + (Y1-Y2)2
second.

3. The diagram below shows the relationship between
the Distance Formula and the coordinates of two
endpoints of a line segment.
 (X1 –X2)2 + (Y1-Y2)2
A
L
E
R
T
!

4. EXAMPLE: Finding the length of
a segment, given its endpoints
 (X1 –X2)2 + (Y1-Y2)2

5. Let’s Practice:
What is the distance between the points
(5, 6) and (– 12, 40) ?

6. Let’s Practice:
Find the lengths of the segments. Tell
whether any of the segments have the same
length. Use the Distance Formula.
A (-1,1)
C (3,2)
AC = ___
A (-1,1)
D (2,-1)
AD = __
A (-1,1)
B (4,3)
AB = ___
AB = 13; AC = 17; AD = 13

7. Now, it’s your turn…..
What is the distance between (–2, 7) and (4, 6)?
6.08
What is your answer? _________
What is the distance between (–1, 1) and (4, 3)?
13
What is your answer? _________
ALGEBRA CHALLENGE: If the distance from (x, 3) to
(4, 7) is 41 , what is the value of x?
9
What is your answer? _________

8. Final Checks for Understanding
1. Find the distance between the two points.
C (0,0)
D (5,2)
2. Use the Distance Formula to determine if
JK = KL.
J(3,-5); K(-1,2) ; L (-5,-5)
_________________________________
J (3,-5)
K (1,2)
K (1,2)
L (-5,-5)
JK=
KL=