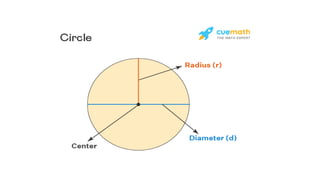
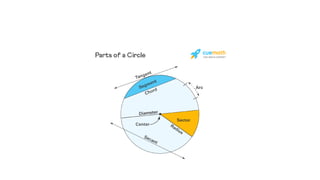
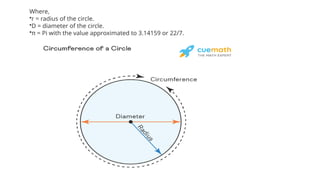
A circle is defined as a 2D figure formed by points equidistant from a center, with key components including circumference, radius, diameter, chord, tangent, secant, arc, segment, and sector. The document explains how to calculate the circumference, radius, and diameter using formulas involving the circle's properties and relevant mathematical constants. Additionally, it covers the characteristics and relationships of other components of a circle, such as chords, tangents, secants, arcs, segments, and sectors.

1. Definition of a Circle
• A circle can be defined as a 2D figure formed by a set of
points that are adjacent to each other and are equidistant
from a fixed point. The fixed point in this curved plane figure
is called the center of the circle, the common distance
between the points from the center is called a radius, and a
line that crosses from the center of the circle starting from
one point to the other is called a diameter. A circle has two
main regions namely, the interior of a circle and the exterior
of a circle. The interior of a circle consists of the region
inside the circle and the exterior of a circle is the region
outside the circle.

3. What are the Parts of a Circle?
• A circle is a closed figure with a curved boundary and has many parts that represent the
properties and characteristics of a circle.
• Circle and its Parts
• The different parts of a circle are listed below:
• Circumference
• Radius
• Diameter
• Chord
• Tangent
• Secant
• Arc
• Segment
• Sector

5. Circumference of a Circle
• The circumference of a circle is its boundary. In other words, when
we measure the boundary or the distance around the circle, that
measure is called the circumference and it is expressed in units of
length like centimeters, meters, or kilometers. The circumference of
a circle has three most important elements namely, the center, the
diameter, and the radius.
• Since we cannot use the ruler (scale) to measure the distance of this
curved figure, we apply a formula that uses the radius, diameter, and
the value of Pi (π). The formulas for the circumference of a circle are
given as follows:
• When the radius is given: Circumference of a circle formula = 2πr
• When the diameter is given: Circumference of a circle formula = π ×
D

6. Where,
•r = radius of the circle.
•D = diameter of the circle.
•π = Pi with the value approximated to 3.14159 or 22/7.

7. Radius of a Circle
• The radius of a circle is the length of the line segment joining the center of the
circle to any point on the circumference of the circle. A circle can have many radii
(the plural form of radius) and they measure the same. Usually, the radius of a
circle is denoted by 'r'.
• To calculate the radius of a circle when the diameter, area of a circle, and
circumference is known, we use the following formulas:
• Radius of Circle = Diameter / 2 - The diameter is twice the length of the radius
and is also the longest chord of the circle. When the diameter is known, we use
this formula.
• Radius of Circle = Circumference / 2π - The circumference is the perimeter of the
circle and when the circumference is given, we use this formula.
• Radius of Circle = √(Area/π) - The area of a circle is the space inside the circle.
Hence, when the area of the circle is given, we use this formula.

8. Diameter of a Circle
• The diameter of a circle is a line segment that passes through the center of the
circle and with endpoints that lie on the circumference of a circle. The diameter is
also known as the longest chord of the circle and is twice the length of the radius.
The diameter is measured from one end of the circle to a point on the other end
of the circle, passing through the center. The diameter is denoted by the letter D.
There can be an infinite number of diameters where the length of each diameter
of the circle is length.
• To calculate the diameter of a circle when the radius, area of a circle, and
circumference is known, we use the following formulas:
• Diameter = Circumference/π (used when the circumference is given)
• Diameter = Radius × 2 (used when the radius is given)
• Diameter = 2√(Area/π) (used when the area of the circle is given)

9. Chord of a Circle
• A chord of a circle is a line segment that joins two points on the circumference
of the circle. A chord divides the circle into two regions known as the segment
of the circle which can be referred to as minor segment and major segment
depending on the area covered by the chord. In a circle, when the chord is
extended infinitely on both sides it becomes a secant. In the figure given
below, PQ is represented as the chord of the circle with O as the center.
• To calculate the chord of a circle, we use two basic formulas:
• Chord Length = 2 × √(r2 − d2) (using perpendicular distance from the center)
• Chord Length = 2 × r × sin(c/2) (using trigonometry)
• Where,
• r is the radius of the circle
• c is the angle subtended at the center by the chord
• d is the perpendicular distance from the chord to the circle center.

10. Tangent of a Circle
• The tangent of a circle is defined as a straight line that touches the
curve of the circle at only one point and does not enter the circle’s
interior. The tangent touches the circle's radius at a right angle. The two
main aspects to remember in the tangent is the slope (m) and a point
on the line. The general equation or formula of the tangent to a circle is:
• The tangent to a circle equation x2 + y2 = a2 for a line y = mx + c is given
by the equation y = mx ± a √[1+ m2]
• The tangent to a circle equation x2+ y2 = a2 at (a1, b1) is xa1 + yb1 = a2.
This means that the equation of the tangent is expressed as xa1 + yb1 =
a2, where a1 and b1 are the coordinates at which the tangent is made.

11. Secant of a Circle
• The secant of a circle is the line that cuts across the circle intersecting the circle at
two distinct points. The difference between a chord and a secant is that a chord is
a line segment whose endpoints are on the circumference of the circle whereas a
secant passes through the circle forming a chord or diameter of the circle.
• There are three secant theorems used in the circle which are given below:
• Theorem 1: When two secants intersect at an exterior point, the product of the
one whole secant segment and its external segment is equal to the product of the
other whole secant segment and its external segment.
• Theorem 2: Two secants can intersect inside or outside a circle.
• Theorem 3: If a secant and a tangent are drawn to a circle from a common
exterior point, then the product of the length of the whole secant segment and
its external secant segment is equal to the square of the length of the tangent
segment.

12. Arc of a Circle
• The arc of a circle is the curved part or a part of the circumference of
a circle. In other words, the curved portion of an object is
mathematically called an arc. The arc of a circle has two arcs namely,
minor arc and major arc. To find the measure of these arcs we need
to find the length of the arc along with the angle suspended by the
arc of any two points. To calculate the length of the arc we use
different formulas based on the unit of the central angle (degrees or
radians). For a circle, the arc length formula is θ times the radius of a
circle. The formulas are:
• Arc Length = θ × r (used for radians)
• Arc Length = θ × (π/180) × r (used for degrees)

13. Segment of a Circle
• A segment of a circle is the region that is bounded by an arc and a
chord of the circle. There are two types of segments - minor segment
and major segment. A minor segment is made by a minor arc and a
major segment is made by a major arc of the circle. To calculate the
segment of a circle, we consider the area of the segment which
consists of a sector (arc + 2 radii) and a triangle. Hence, the formula
for the area of a segment can be expressed as follows
• Area of a segment of circle = area of the sector - area of the triangle
• Note: To find the area of the major segment of a circle, we just
subtract the corresponding area of the minor segment from the total
area of the circle.

14. Sector of a Circle
• A sector of a circle is a pie-shaped part of a circle made of the arc along with its two
radii dividing the circle into a minor sector and a major sector. The larger portion of
the circle is called the major sector whereas the smaller portion of the circle is called
the minor sector. The 2 radii meet at the part of the circumference of a circle known
as an arc, forming a sector of a circle. The formulas to calculate the sector of the
circle are:
• Area of a sector (A) = (θ/360°) × πr2 (when the angle is given)
• Length of a section (l) = (θπr) /180 (when the length is given)
• Area of a sector of a circle = (l × r)/2 (when the length and radius is given)
• Perimeter of a sector of a circle = 2 Radius + ((θ/360) × 2πr )
• Where,
• r = radius of the circle.
• l = length of the arc.
• θ = angle in degrees.
• π = Pi with the value approximated to 3.14159 or 22/7.