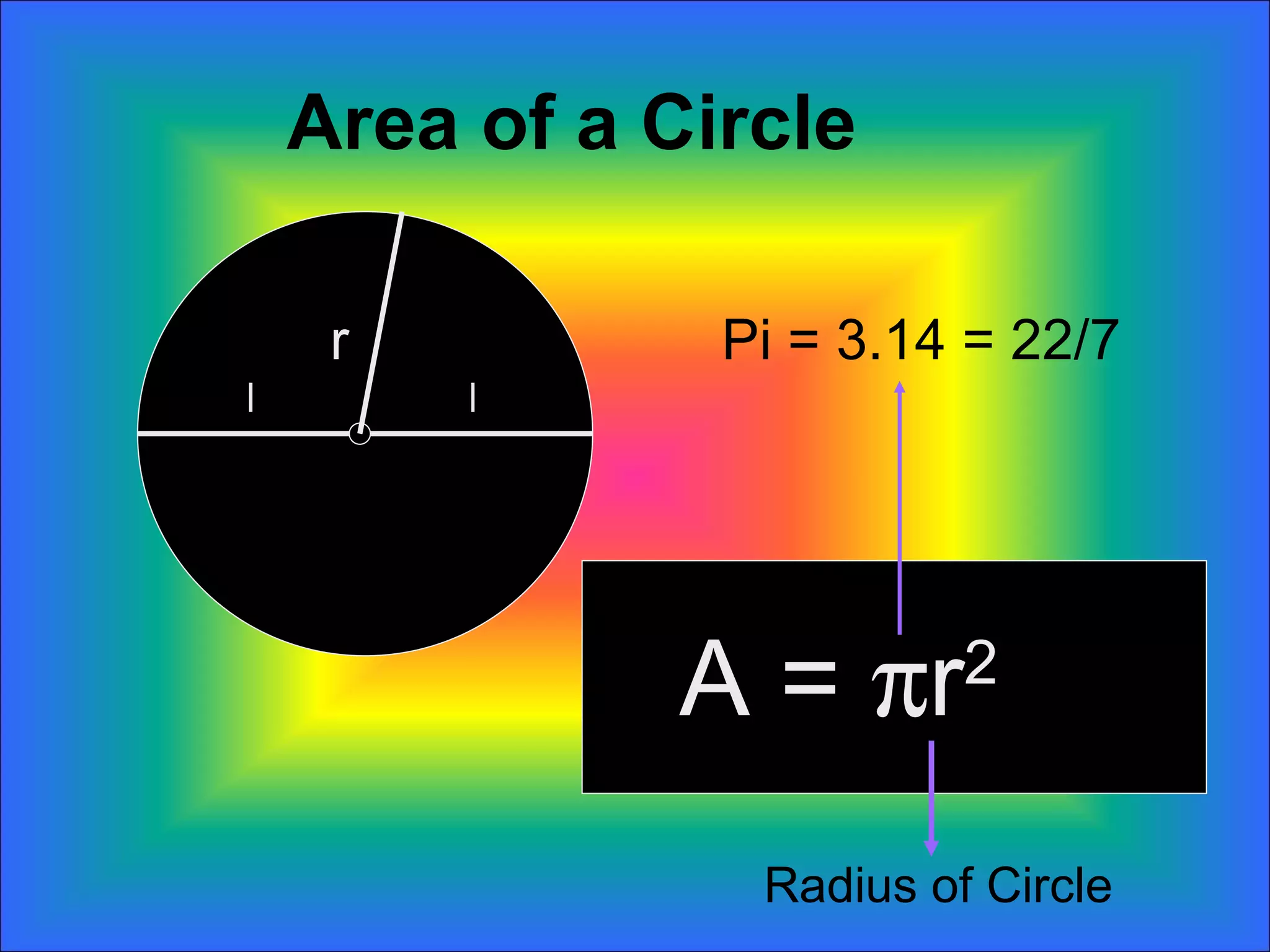
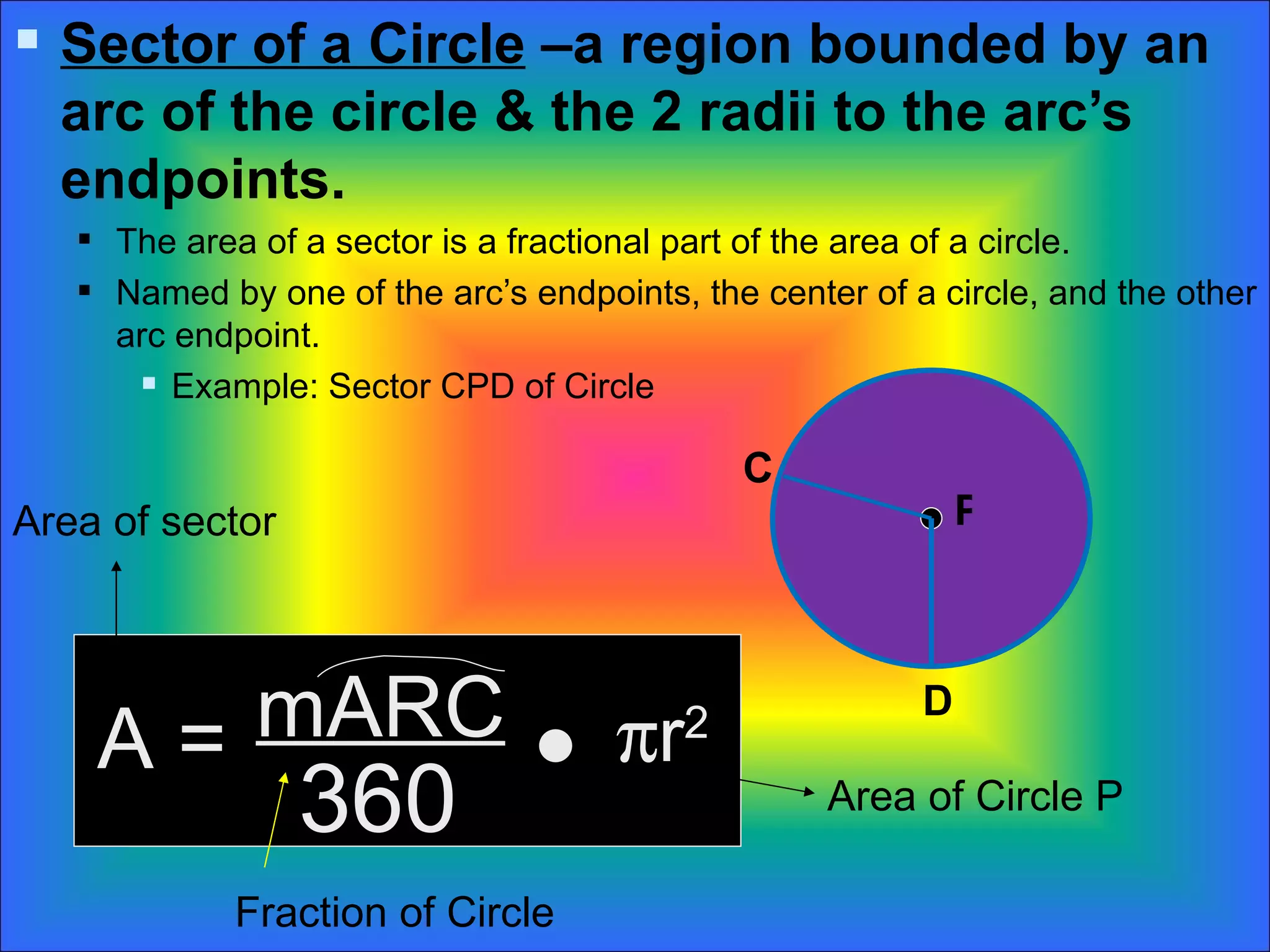
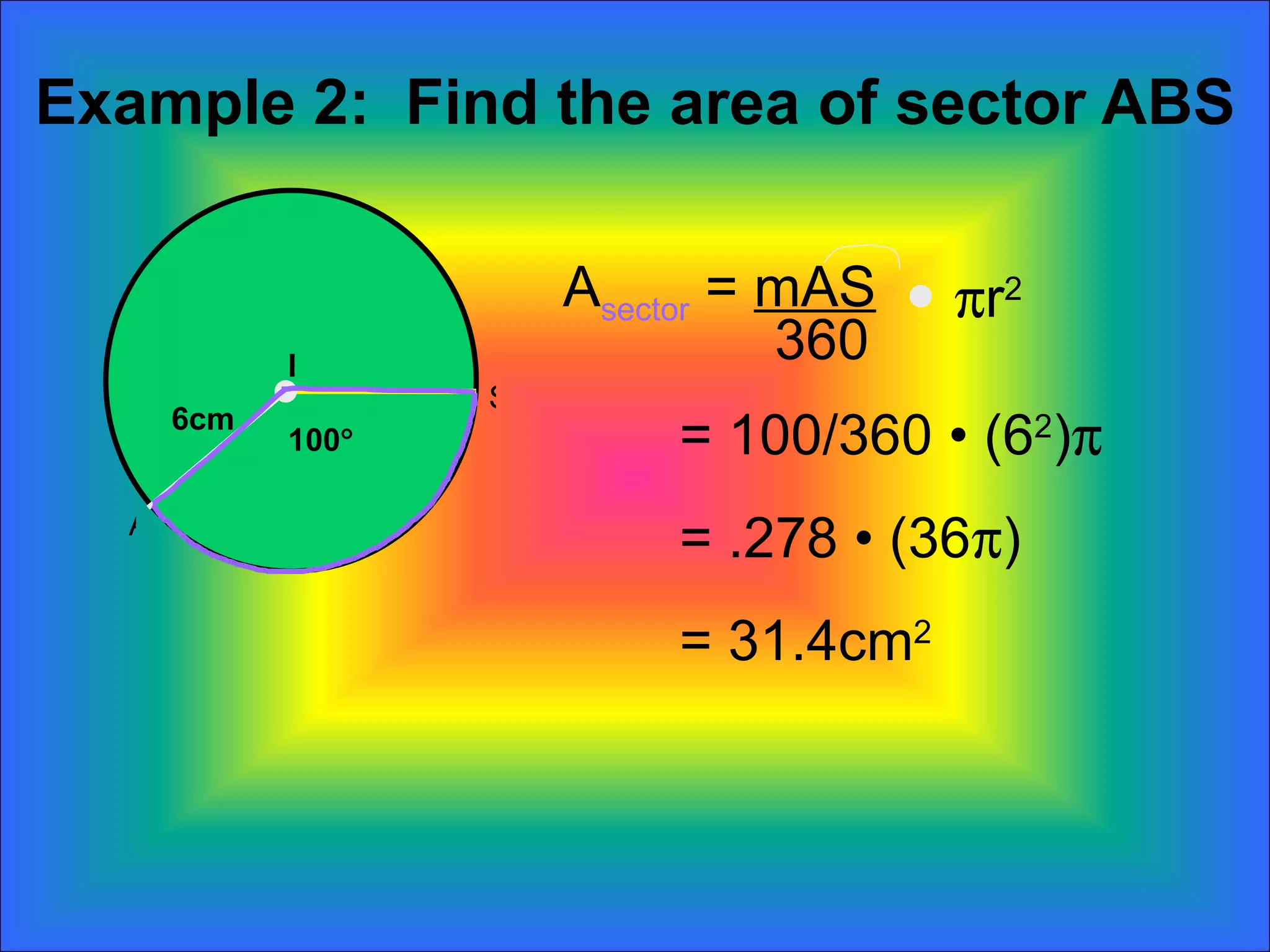
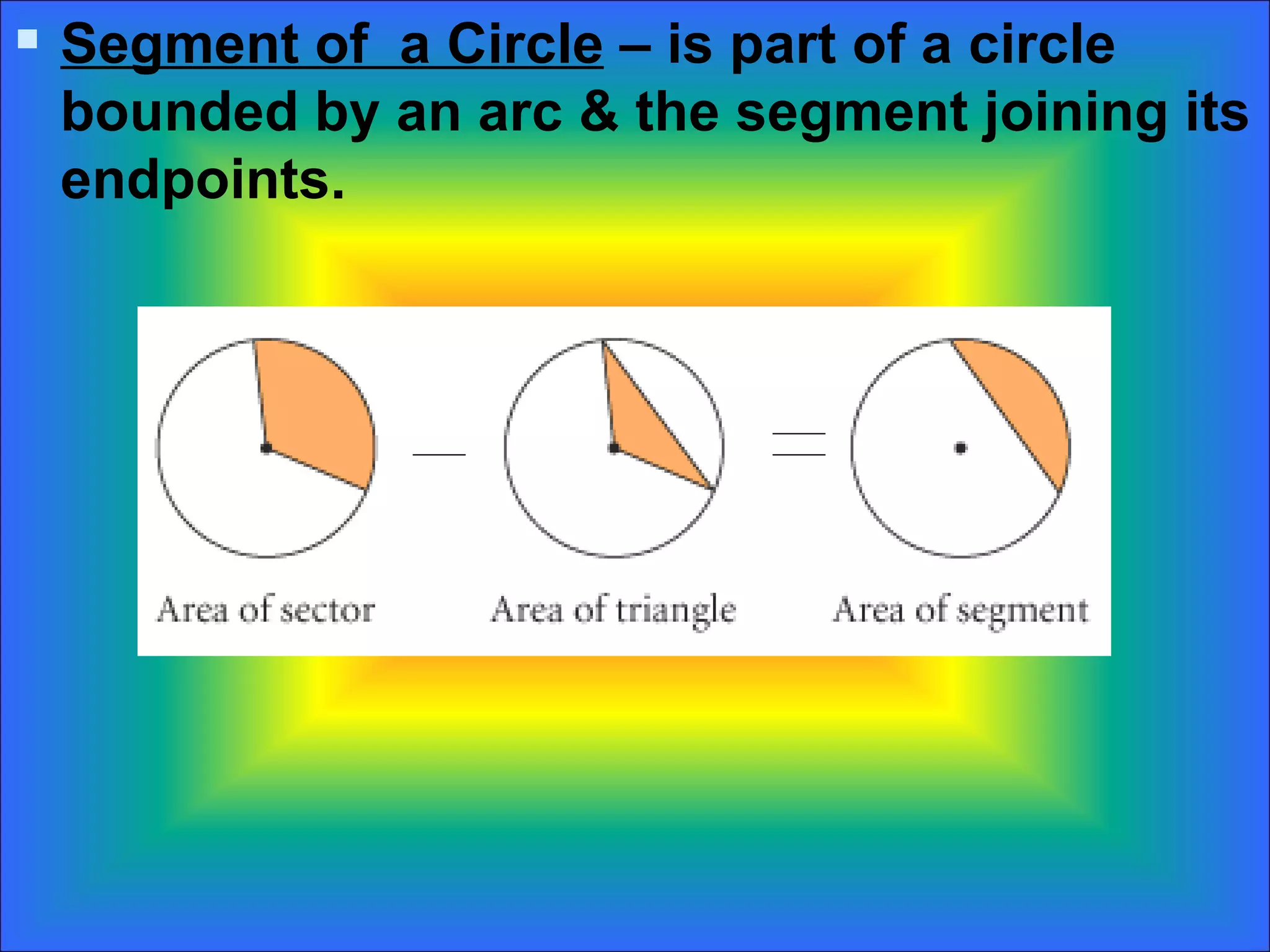
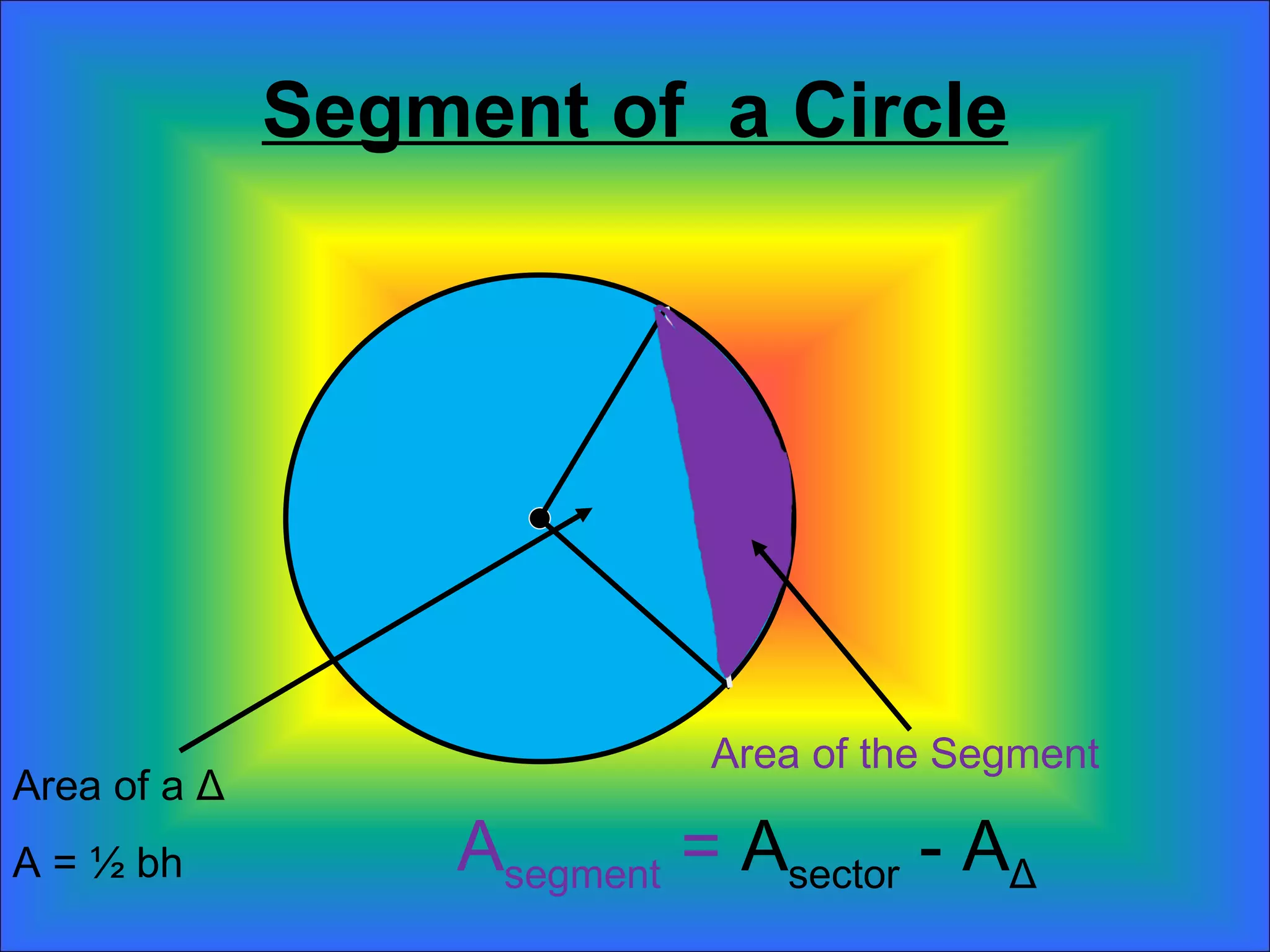
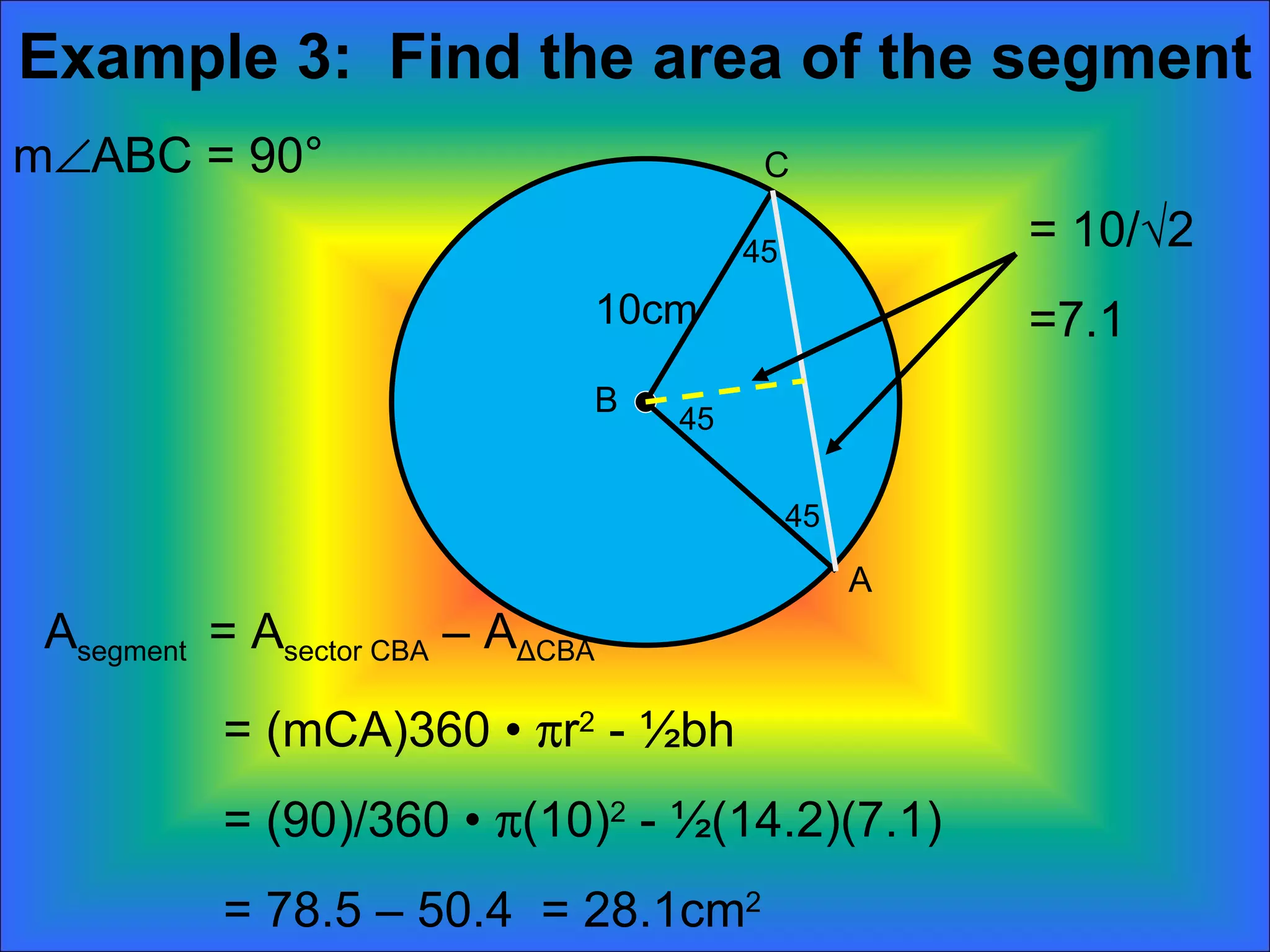
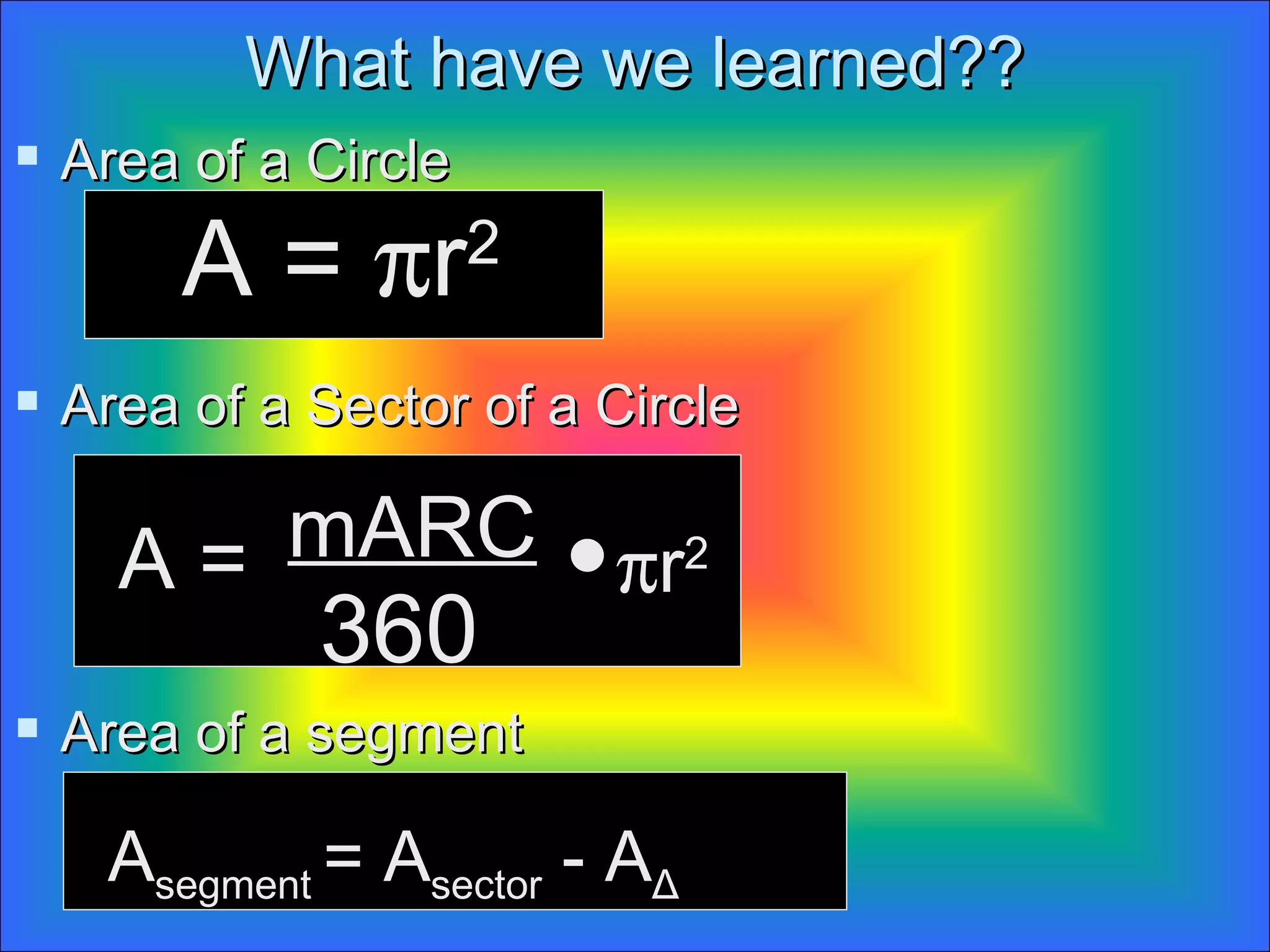
The document discusses calculating the areas of circles, sectors, and segments of circles. It defines a circle as having the area of πr^2, a sector as a fractional part of the total circle area defined by an arc and its radii, and a segment as the portion of a sector minus the area of the triangle formed by the arc and its radii. It provides examples of calculating the areas of full circles, sectors of varying central angles, and segments.

1. Sec. 7 – 7 Areas of Circles & Sectors Objective: To find the areas of circles, sectors and segments of circles

2. Area of a Circle r r A =  r 2 Pi = 3.14 = 22/7 Radius of Circle r

3. Example1: How much more pizza is in a 12in diameter pizza than in a 10in diameter pizza? A 12 =  r 2 = 6 2  = 36  = 113.1in 2 A 10 =  r 2 =5 2  = 25  = 78.5in 2 36  - 25  = 11  = 34.6in 2

4. Sector of a Circle –a region bounded by an arc of the circle & the 2 radii to the arc’s endpoints. The area of a sector is a fractional part of the area of a circle. Named by one of the arc’s endpoints, the center of a circle, and the other arc endpoint. Example: Sector CPD of Circle C P D A = mARC 360  r 2 Area of sector Fraction of Circle Area of Circle P

5. Example 2: Find the area of sector ABS 100  6cm A sector = mAS 360  r 2 = 100/360 • (6 2 )  = .278 • (36  ) = 31.4cm 2 B A S

6. Segment of a Circle – is part of a circle bounded by an arc & the segment joining its endpoints.

7. Segment of a Circle Area of a Δ A = ½ bh Area of the Segment A segment = A sector - A Δ

8. Example 3: Find the area of the segment m  ABC = 90 ° C B A 45 45 A segment = A sector CBA – A Δ CBA = (mCA)360 •  r 2 - ½bh = (90)/360 •  (10) 2 - ½(14.2)(7.1) = 78.5 – 50.4 = 28.1cm 2 10cm 45 = 10/ √2 =7.1

9. What have we learned?? Area of a Circle Area of a Sector of a Circle Area of a segment A = mARC 360  r 2 A segment = A sector - A Δ A =  r 2 A =  r 2