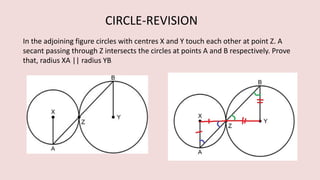
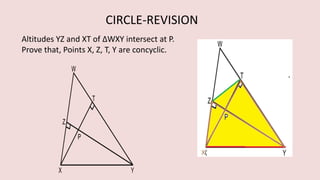
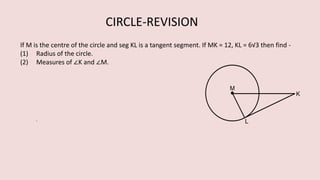
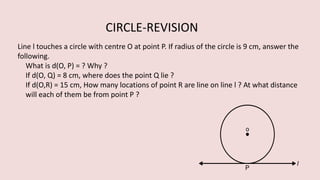
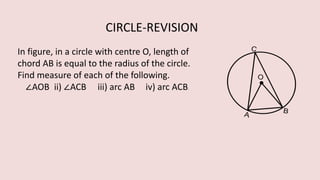
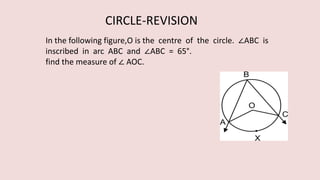
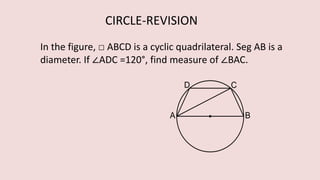
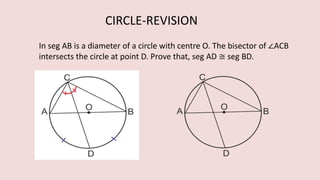
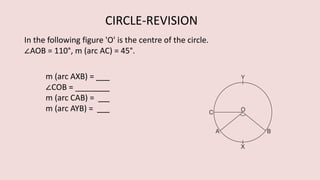
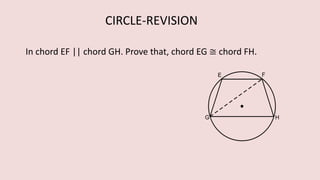
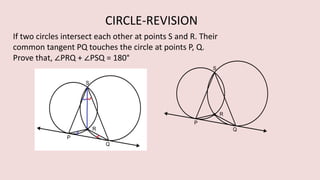
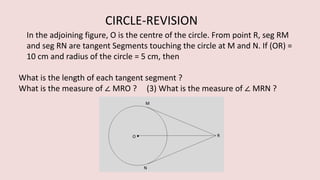
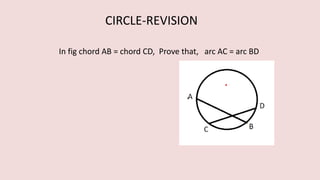
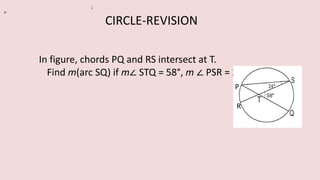
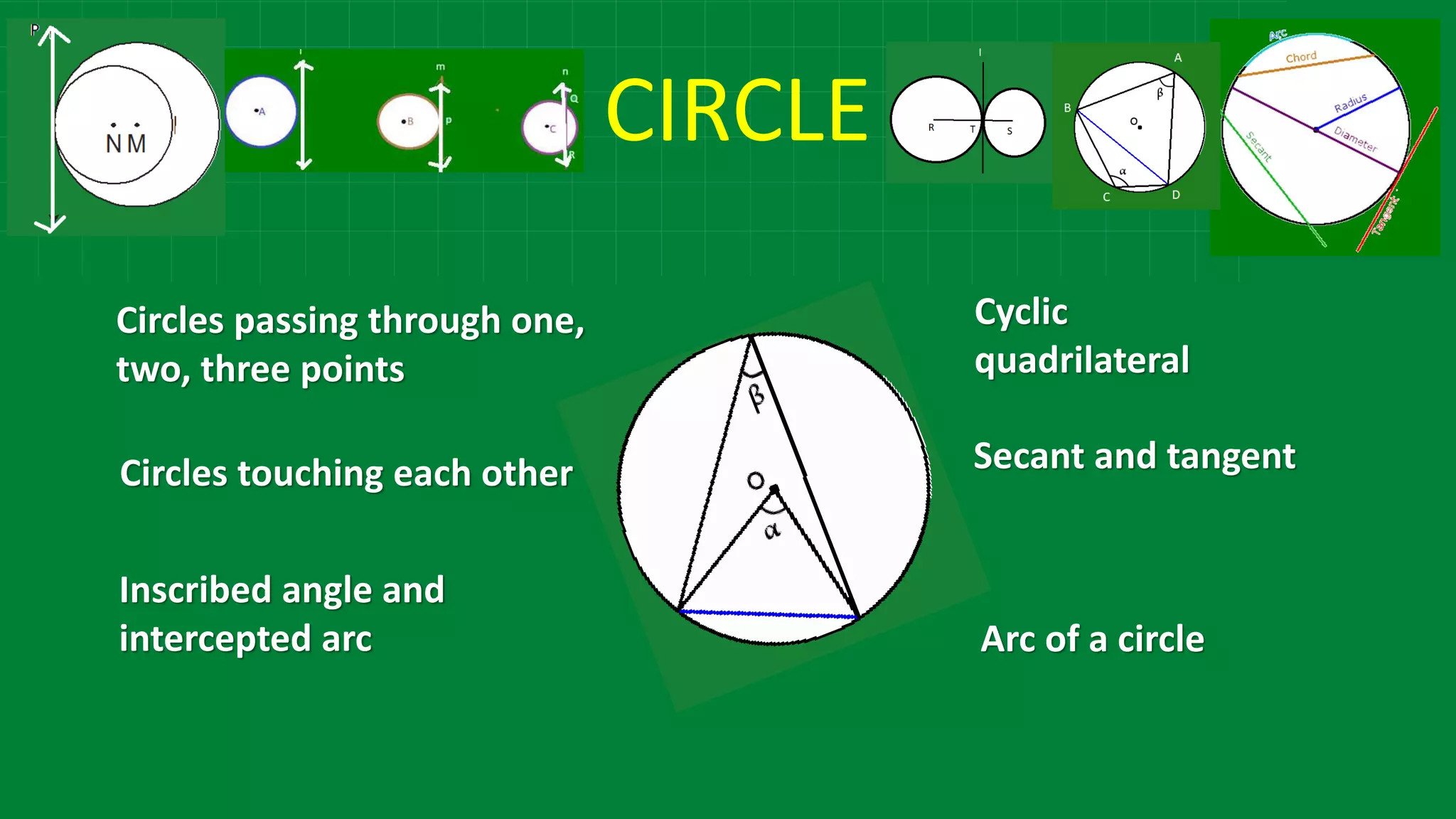
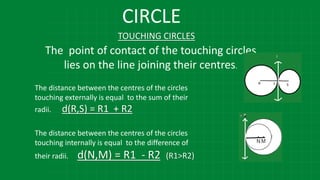
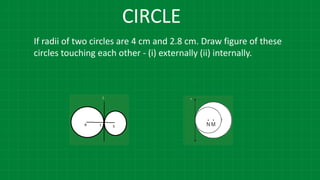
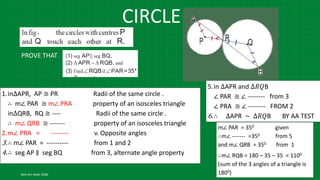
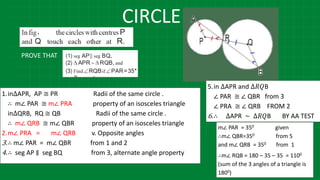
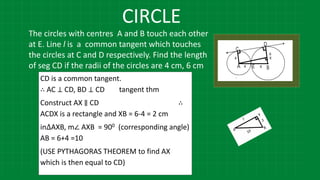
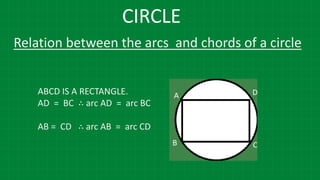
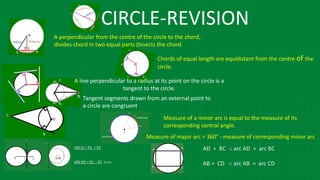
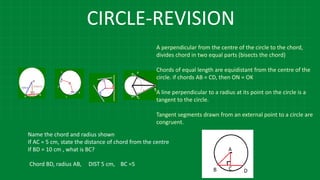
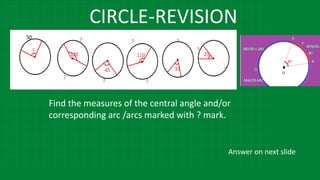
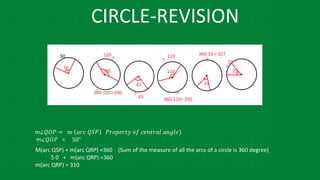
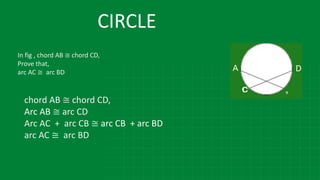
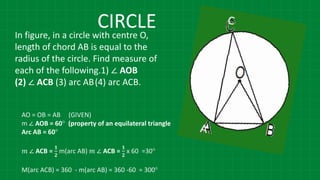
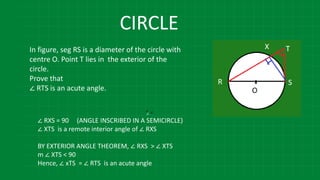
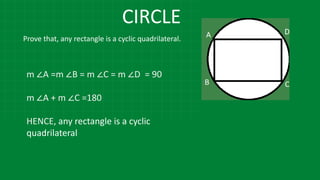
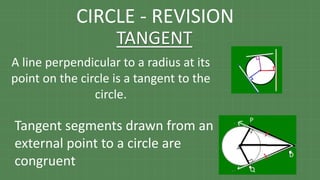
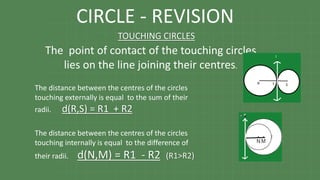
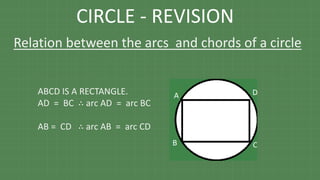
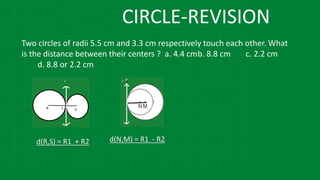
The document details various properties and theorems related to circles, such as chords, tangents, inscribed angles, and relationships between arcs and central angles. It includes formulas related to properties of chords, tangent segments, and the distances between circles, both touching externally and internally. Additionally, it presents problems and solutions involving these concepts, reinforcing the fundamental principles of circular geometry.
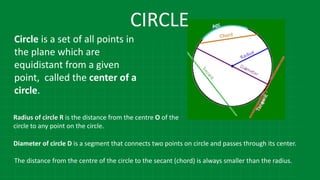

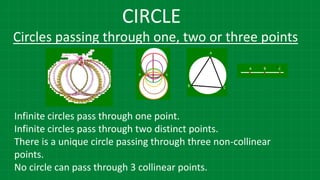
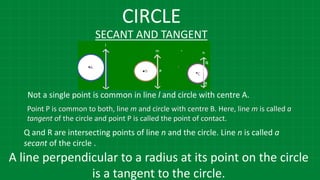
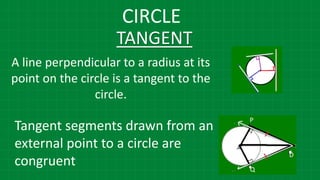





![CIRCLE
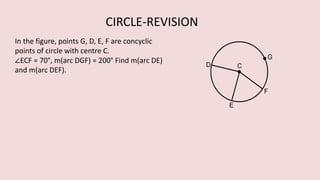
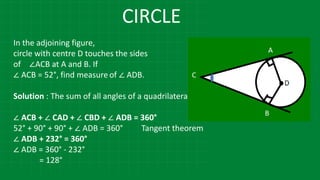
In figure, points G, D, E, F
are concyclic points of a circle with
centre C.
∠ ECF = 70°, m(arc DGF) = 200°
find m(arc DE) and m(arc DEF).
E F
∠ ECF = m (arc EF)
70° = m (arc EF)
m(arc DE) = 360 - [ m (arc DGF + m (arc EF)]
m(arc DE) = 360 – (200° + 70° ) = 90°
m(arc DEF) = m(arc DE) + m (arc EF)
= 90 + 70 = 160°](https://image.slidesharecdn.com/3circle-1-210124151800/85/3-circle-1-24-320.jpg)


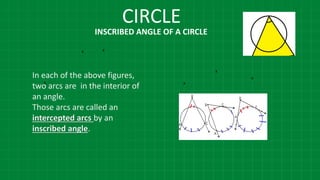

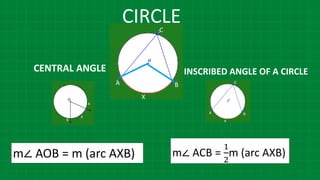
![CIRCLE
∠ AEC = [m(arc AC) + m(arc DB)]
∠ BED = [m(arc BD) - m(arc AC)]
1
2
1
2
1
2
∠ ACB = [m(arc AXB)
1
2
∠ CEB = [m(arc AD) + m(arc CB)]](https://image.slidesharecdn.com/3circle-1-210124151800/85/3-circle-1-38-320.jpg)
![CIRCLE
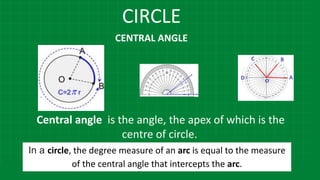
The measure of an inscribed angle is half the measure
of the arc intercepted by it.
Angles inscribed in the same arc are congruent.
Angle inscribed in a semicircle is a right angle.
Opposite angles of a cyclic quadrilateral are supplementary.
∠ BED = [m(arc BD) - m(arc AC)]
∠ AEC = [m(arc AC) + m(arc DB)] and ∠ CEB = [m(arc AD) + m(arc CB)]
1
2
1
2
1
2](https://image.slidesharecdn.com/3circle-1-210124151800/85/3-circle-1-39-320.jpg)
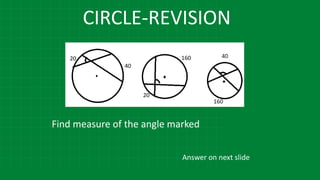
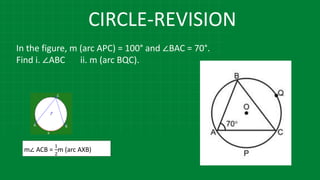
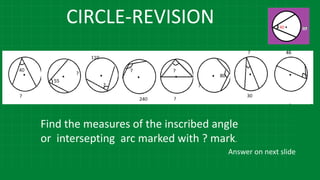
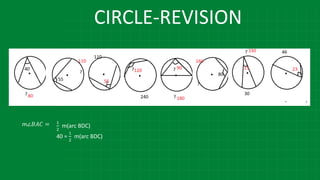
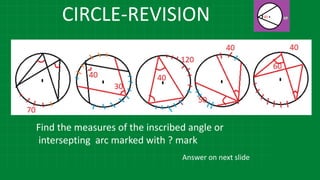
![CIRCLE-REVISION
m∠𝑄𝑂𝑅 = 1
2
[20+40]
m∠𝑄𝑂𝑅 = 1
2
[m(arc QR) + m(arc WE)](https://image.slidesharecdn.com/3circle-1-210124151800/85/3-circle-1-43-320.jpg)
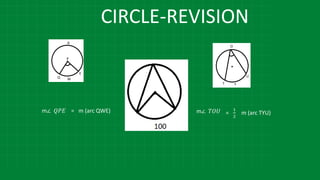
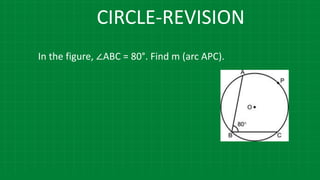
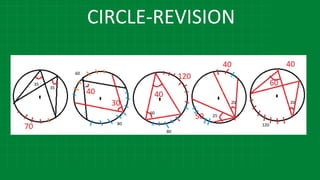
![CIRCLE-REVISION
m∠𝑄𝑃𝑊 =
1
2
[ m (arc QTW) + m (arc RTE)] m∠ 𝐷𝐹𝐺 =
1
2
[ m (arc SH) - m(arc DG)]
m∠ WPE =
1
2
[ m (arc WE) + m (arc QR)]](https://image.slidesharecdn.com/3circle-1-210124151800/85/3-circle-1-45-320.jpg)

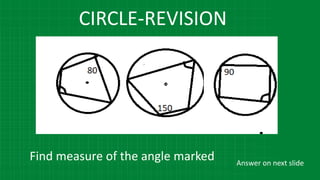
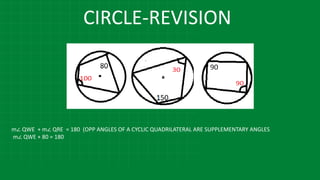




![CIRCLE
In figure, m(arc NS) = 125°,
m(arc EF) = 37°, find the measure NMS.
M
∠ NMS = [125°- 37°)]
1
2
∠ NMS = [m(arc NS) - m(arc EF)]
1
2
∠ NMS = [88°]
∠ NMS = 44°
1
2](https://image.slidesharecdn.com/3circle-1-210124151800/85/3-circle-1-58-320.jpg)
![CIRCLE
A E
In figure, chords AC and DE
intersect at B. If ABE = 108°,
m(arc AE) = 95°, find m(arc DC)
∠ ABE = [m(arc AE) + m(arc DC)]
108° X 2 = [95° + m(arc DC]
216-95 = m(arc DC)
131° = m(arc DC)
1
2](https://image.slidesharecdn.com/3circle-1-210124151800/85/3-circle-1-59-320.jpg)



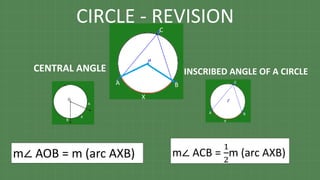
![CIRCLE
The measure of an inscribed angle is half the measure
of the arc intercepted by it.
Angles inscribed in the same arc are congruent.
Angle inscribed in a semicircle is a right angle.
Opposite angles of a cyclic quadrilateral are supplementary.
∠ BED = [m(arc BD) - m(arc AC)]
∠ AEC = [m(arc AC) + m(arc DB)] and ∠ CEB = [m(arc AD) + m(arc CB)]
1
2
1
2
1
2](https://image.slidesharecdn.com/3circle-1-210124151800/85/3-circle-1-67-320.jpg)

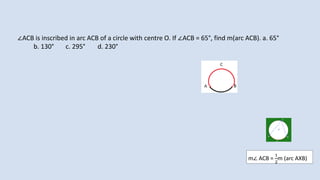
![1 From the information given in the figure, find the measure of ∠AEC. a. 42° b. 30°
c. 36° d. 72°
𝐻𝐼𝑁𝑇: ∠ AEC = [m(arc AC) + m(arc DB)] and ∠ CEB = [m(arc AD) + m(arc CB)]
1
2
1
2](https://image.slidesharecdn.com/3circle-1-210124151800/85/3-circle-1-70-320.jpg)
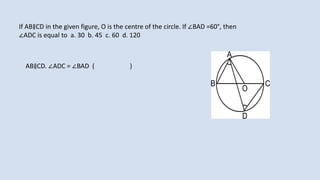

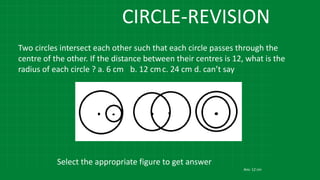

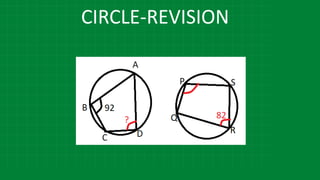
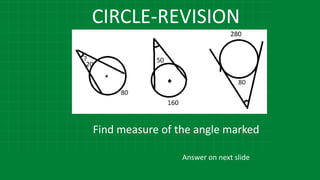
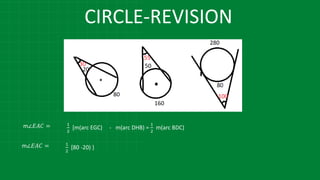
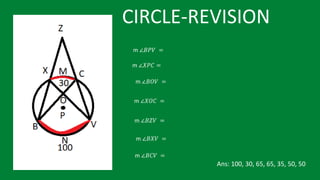
![CIRCLE-REVISION
∠
2
∠
1.In the figure m (arc LN) = 110°, m (arc PQ) = 50° find ∠LMN.
LMN = 1 [m (arc LN) - [ ]
2
∠ BED =
1
2
[m(arc BD) - m(arc AC)]](https://image.slidesharecdn.com/3circle-1-210124151800/85/3-circle-1-76-320.jpg)

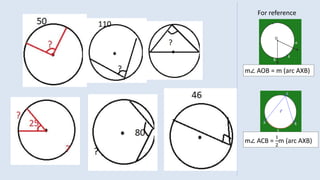
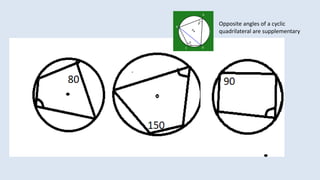
![𝐻𝐼𝑁𝑇: ∠ interior =
1
2
[m(arc 1) + m(arc 2)]
∠ exterior =
1
2
[m(arc 1) - m(arc 2)]](https://image.slidesharecdn.com/3circle-1-210124151800/85/3-circle-1-80-320.jpg)