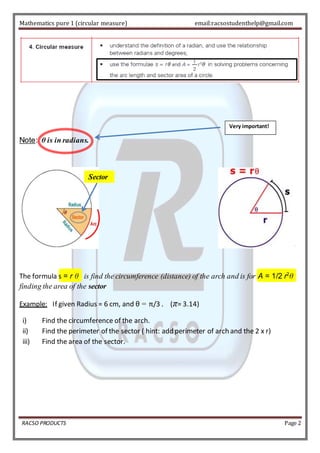
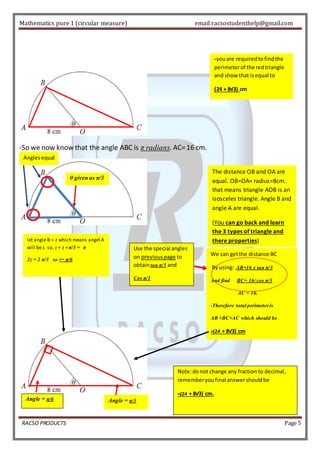
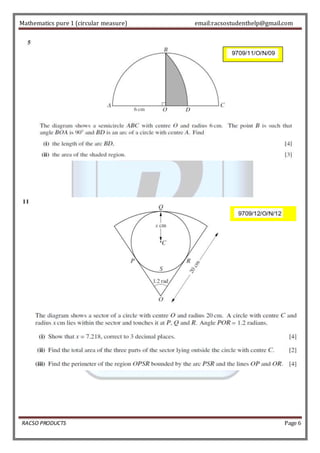
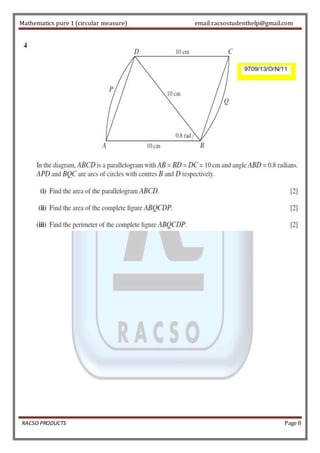
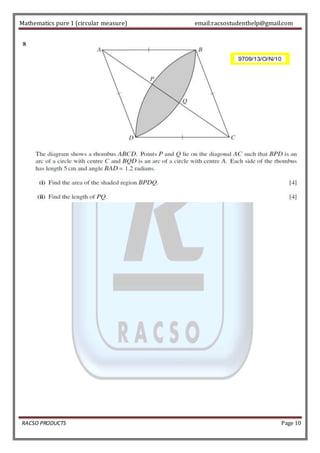
The document defines a radian as the angle subtended by an arc of a circle equal in length to the radius. It states that π radians equals 180 degrees, so 1 radian equals about 57.29 degrees. Formulas are provided for finding the circumference of an arc and area of a sector using radians. Examples are given to practice converting between radians and degrees and using the formulas. Special angle values are listed in a table. Past exam questions are worked through, applying concepts of radians, sectors, arcs, and right triangles in semi-circles.