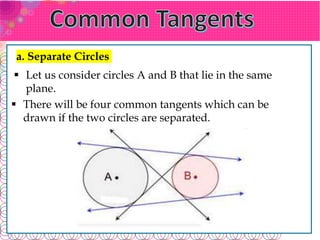
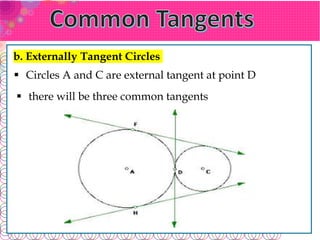
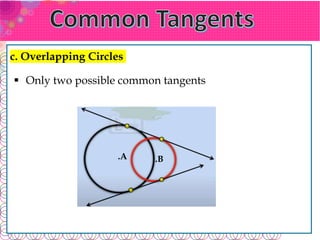
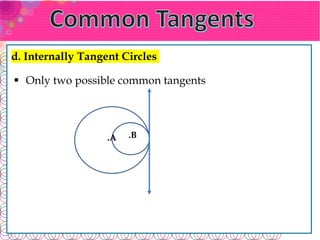
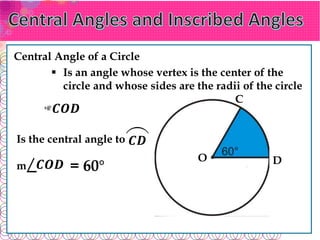
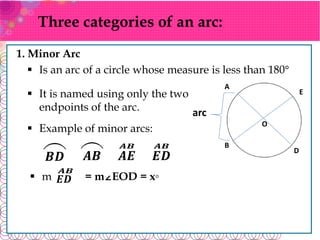
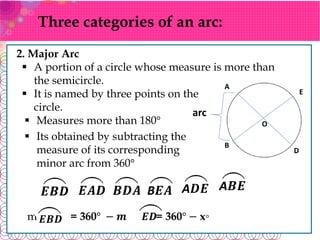
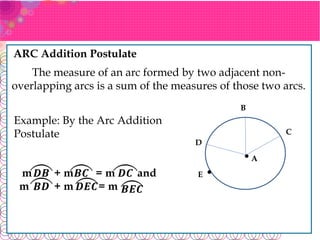
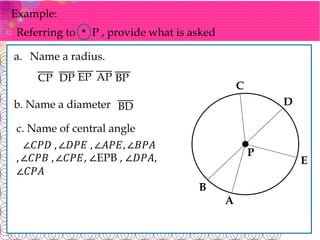
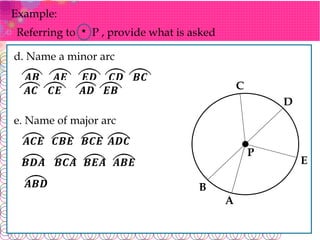
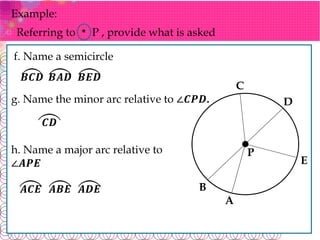
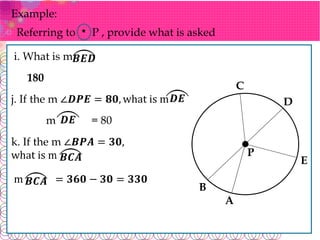
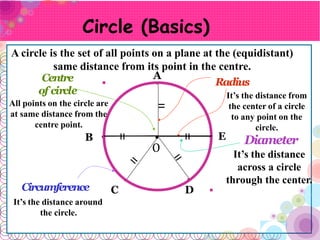
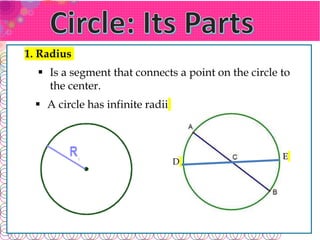
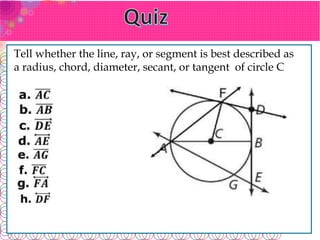
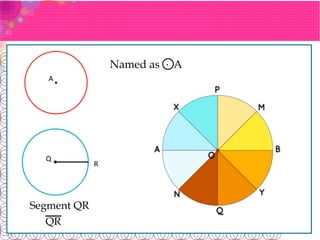
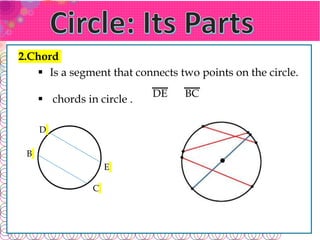
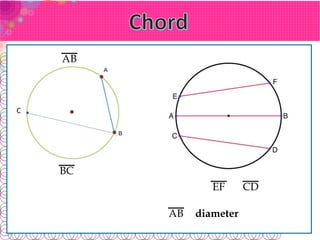
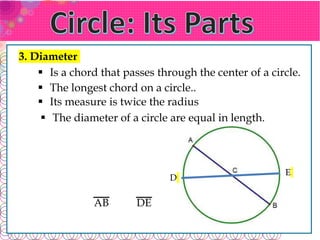
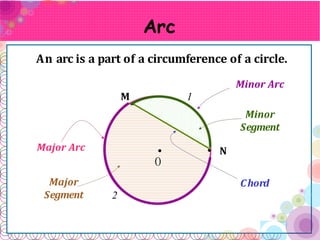
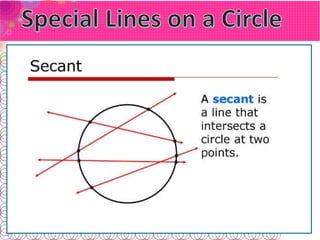
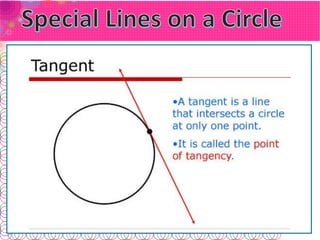
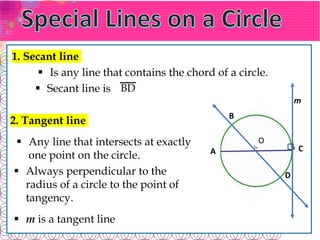
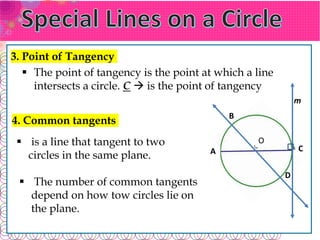
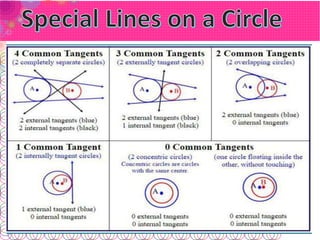
The document defines key terms related to circles: - A circle is a set of points equidistant from a fixed center point. A radius connects the center to any point on the circle. - A chord connects two points on the circle. The longest chord, called the diameter, passes through the center. - A secant line contains a chord. A tangent line intersects at just one point and is perpendicular to the radius at that point. 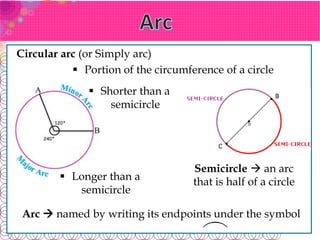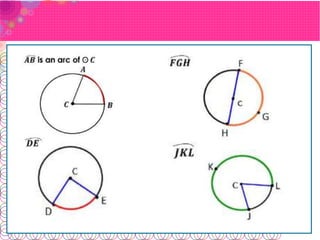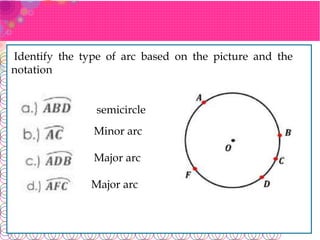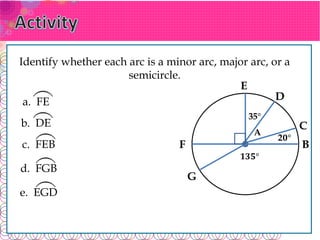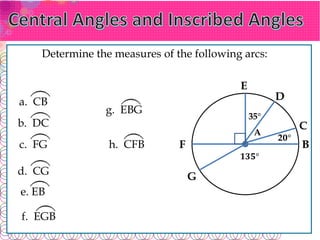- An arc is part of a circle's circumference. Arcs are classified as minor, major, or semicircles based on their angle measure. 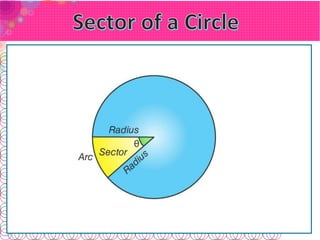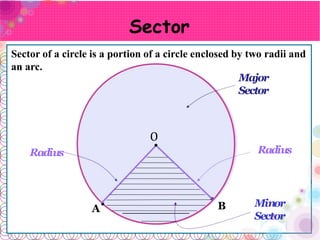- A sector is the region within an arc and its enclosing radii. The central angle at the center defines

2. CIRCLE

3. Circle
 Defined as a locus of points that are equidistant
from a given fixed point in the plane.
 The given fixed point in the plane is called the center
 A Circle is named using the center.

4. Circle (Basics)
O
=
=
=
A
C D
B
A circle is the set of all points on a plane at the (equidistant)
same distance from its point in the centre.
Radius
It’s the distance from
the center of a circle
to any point on the
circle.
E
Centre
of circle
All points on the circle are
at same distance from the
centre point.
Circumference
It’s the distance around
the circle.
Diameter
It’s the distance
across a circle
through the center.

5. 1. Radius
 Is a segment that connects a point on the circle to
the center.
 A circle has infinite radii
D
E

6. A
Named as A
.
Q
R
Segment QR
QR

7. 2.Chord
 Is a segment that connects two points on the circle.
D
E
DE
 chords in circle .
B
C
BC

8. Chord
O
A
E
B
Chord Chord
Diameter,
the biggest chord
Interior of
the circle
Exterior of the circle
A chord of a circle is a line segment whose endpoints are points
on the circle.

9. AB
C
BC
EF
AB
CD
diameter

10. 3. Diameter
 Is a chord that passes through the center of a circle.
 The longest chord on a circle..
D
E
AB DE
 Its measure is twice the radius
 The diameter of a circle are equal in length.

14. 1. Secant line
 Is any line that contains the chord of a circle.
A C
O
B
D
 Secant line is BD
2. Tangent line
 Any line that intersects at exactly
one point on the circle.
 Always perpendicular to the
radius of a circle to the point of
tangency.
m
 m is a tangent line

15. 3. Point of Tangency
 The point of tangency is the point at which a line
intersects a circle. C  is the point of tangency
A C
O
B
D
4. Common tangents
 is a line that tangent to two
circles in the same plane.
m
 The number of common tangents
depend on how tow circles lie on
the plane.

16. a. Separate Circles
 Let us consider circles A and B that lie in the same
plane.
 There will be four common tangents which can be
drawn if the two circles are separated.

17. b. Externally Tangent Circles
 Circles A and C are external tangent at point D
 there will be three common tangents

18. c. Overlapping Circles
 Only two possible common tangents
.A .B

19. d. Internally Tangent Circles
 Only two possible common tangents
.A .B

20. e. Concentric Circles
 Circles which have the same center.
.A
 No common tangent

22. Tell whether the line, ray, or segment is best described as
a radius, chord, diameter, secant, or tangent of circle C

23. Arc
O
N
Chord
Major Arc
Major
Segment
An arc is a part of a circumference of a circle.
Minor Arc
M 1
Minor
Segment
2

24. Circular arc (or Simply arc)
 Portion of the circumference of a circle
 Shorter than a
semicircle
 Longer than a
semicircle
Semicircle  an arc
that is half of a circle
Arc  named by writing its endpoints under the symbol

26. Identify the type of arc based on the picture and the
notation
semicircle
Minor arc
Major arc
Major arc

28. Sector
A B
Radius Radius
Minor
Sector
Sector of a circle is a portion of a circle enclosed by two radii and
an arc.
Major
Sector
O

29. Central Angle of a Circle
 Is an angle whose vertex is the center of the
circle and whose sides are the radii of the circle
C
D
O
Is the central angle to 𝑪𝑫
𝑪𝑶𝑫
m = 60°
𝑪𝑶𝑫

30. A
E
O
B
D
arc
Three categories of an arc:
1. Minor Arc
 Is an arc of a circle whose measure is less than 180°
 It is named using only the two
endpoints of the arc.
 Example of minor arcs:
𝑩𝑫 𝑨𝑩 𝑨𝑬 𝑬𝑫
 m = m∠EOD = x◦
𝑬𝑫

31. A
E
O
B
D
arc
Three categories of an arc:
2. Major Arc
 A portion of a circle whose measure is more than
the semicircle.
 It is named by three points on the
circle.
𝑬𝑩𝑫 𝑬𝑨𝑫 𝑩𝑫𝑨 B𝑬𝑨
m = 360° − 𝒎 = 360° − x◦
𝑬𝑩𝑫
 Measures more than 180°
 Its obtained by subtracting the
measure of its corresponding
minor arc from 360°
A𝑫𝑬 A𝑩𝑬
𝑬𝑫

32. A
E
O
B
D
arc
Three categories of an arc:
3. Semicircle
 An arc whose measure is exactly 180°
 Its endpoints are the endpoints of
the diameter.
𝑨𝑩𝑫 𝑩𝑫𝑬 𝑫𝑬𝑨 EAB
m = 1𝟖𝟎°
𝑨𝑩𝑫
 It is named using the two
endpoints and a points and a
point in between the
endpoints

33. 𝑬𝑮
𝑬𝑹𝑮
𝑬𝑮
The measure of the central angle is equal to the
measure of its intercepted arc
88°
E
G
Q
R
𝑬𝑹𝑮
𝑬𝑮
Given circle Q, find m
and m
Solution:
m∠EQG = 88° , m = 88°
m = 360° − m
= 360° − 𝟖𝟖° = 𝟐𝟕𝟐°

34. 𝑩𝑬𝑪
𝑫𝑬𝑪
𝑩𝑫
𝑫𝑪
𝑩𝑪
𝑫𝑩
ARC Addition Postulate
The measure of an arc formed by two adjacent non-
overlapping arcs is a sum of the measures of those two arcs.
A
B
C
D
E
m + m = m and
m + m = m
Example: By the Arc Addition
Postulate

35. Example:
Referring to P , provide what is asked
.
a. Name a radius.
C
D
E
A
B
P
CP DP EP AP BP
b. Name a diameter BD
c. Name of central angle
∠𝐶𝑃𝐷 , ∠𝐷𝑃𝐸 , ∠𝐴𝑃𝐸, ∠𝐵𝑃𝐴
, ∠𝐶𝑃𝐵 , ∠𝐶𝑃𝐸, ∠EPB , ∠𝐷𝑃𝐴,
∠𝐶𝑃𝐴

36. Example:
Referring to P , provide what is asked
.
d. Name a minor arc
C
D
E
A
B
P
e. Name of major arc
𝑨𝑩 𝑨𝑬 𝑬𝑫 𝑪𝑫 𝑩𝑪
𝑨𝑪 𝑪𝑬 𝑨𝑫 𝑬𝑩
𝑨𝑪𝑬 𝑪𝑩𝑬 𝑩𝑪𝑬 𝑨𝑫𝑪
𝑩𝑫𝑨 𝑩𝑪𝑨 𝑩𝑬𝑨 𝑨𝑩𝑬
𝑨𝑩𝑫

37. Example:
Referring to P , provide what is asked
.
f. Name a semicircle
C
D
E
A
B
P
g. Name the minor arc relative to ∠𝑪𝑷𝑫.
𝑩𝑪𝑫 𝑩𝑨𝑫 𝑩𝑬𝑫
𝑪𝑫
h. Name a major arc relative to
∠𝑨𝑷𝑬
𝑨𝑪𝑬 𝑨𝑩𝑬 𝑨𝑫𝑬

38. 𝑩𝑬𝑫
Example:
Referring to P , provide what is asked
.
i. What is m
C
D
E
A
B
P
𝑫𝑬
j. If the m ∠𝑫𝑷𝑬 = 𝟖𝟎, what is m
180
𝑫𝑬
m = 80
k. If the m ∠𝑩𝑷𝑨 = 𝟑𝟎,
what is m 𝑩𝑪𝑨
𝑩𝑪𝑨
m = 𝟑𝟔𝟎 − 𝟑𝟎 = 𝟑𝟑𝟎

39. Identify whether each arc is a minor arc, major arc, or a
semicircle.
D
A
F B
a. FE
C
E
G
35°
2𝟎°
1𝟑𝟓°
b. DE
c. FEB
d. FGB
e. EGD

40. Determine the measures of the following arcs:
D
A
F B
a. CB
C
E
G
35°
2𝟎°
1𝟑𝟓°
b. DC
e. EB
f. EGB
g. EBG
h. CFB
c. FG
d. CG