Embed presentation
Downloaded 61 times





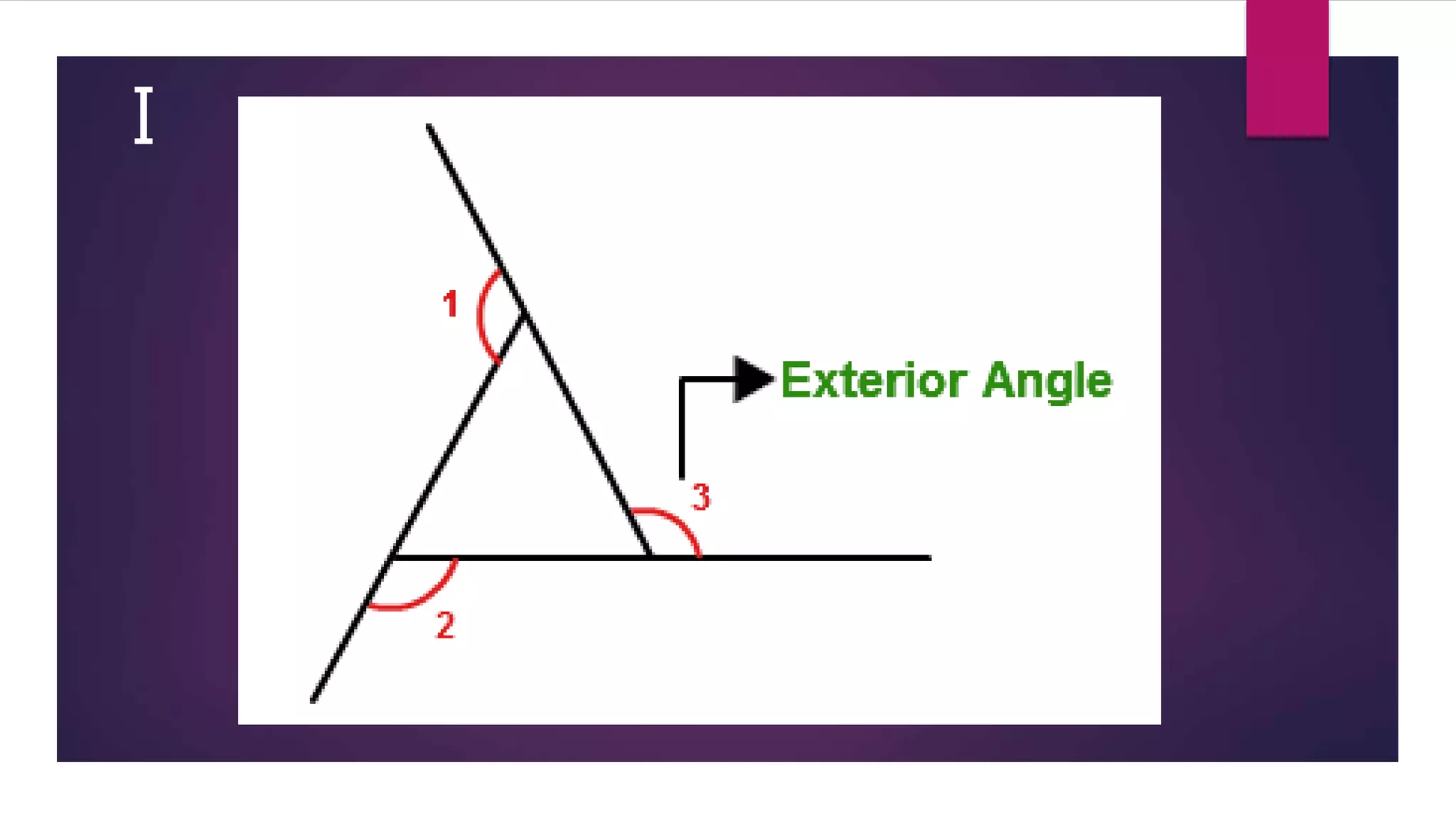
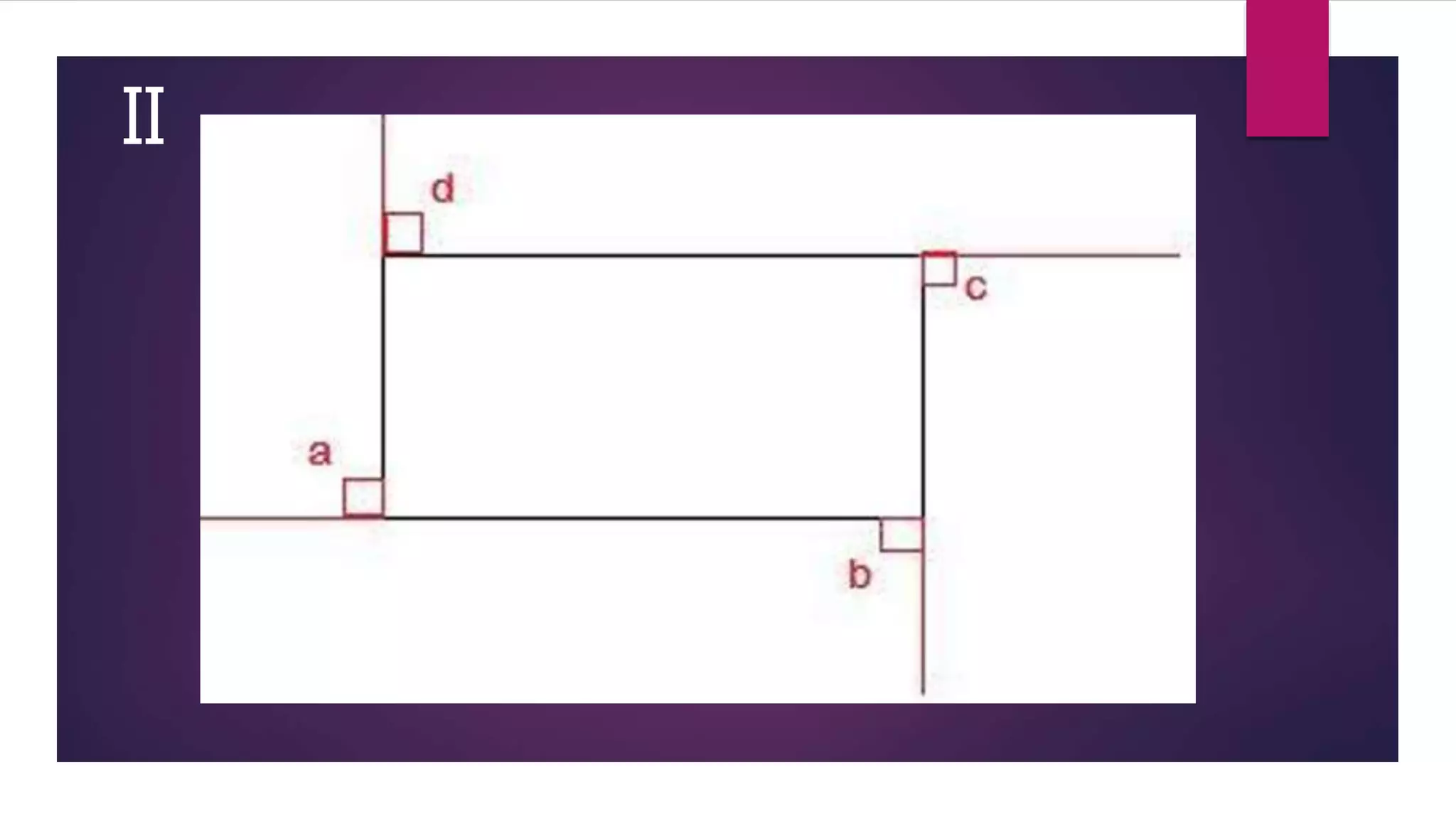
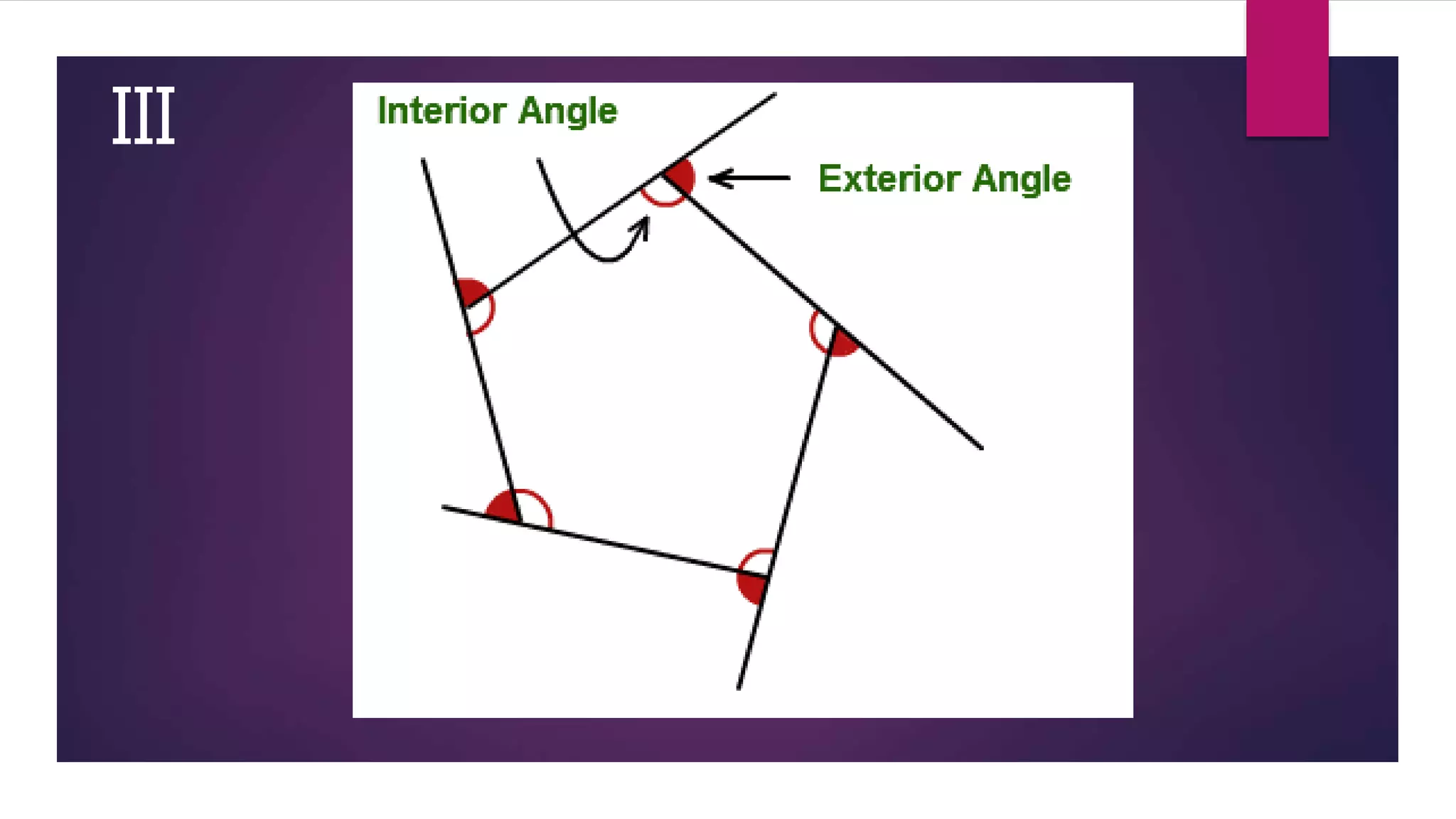
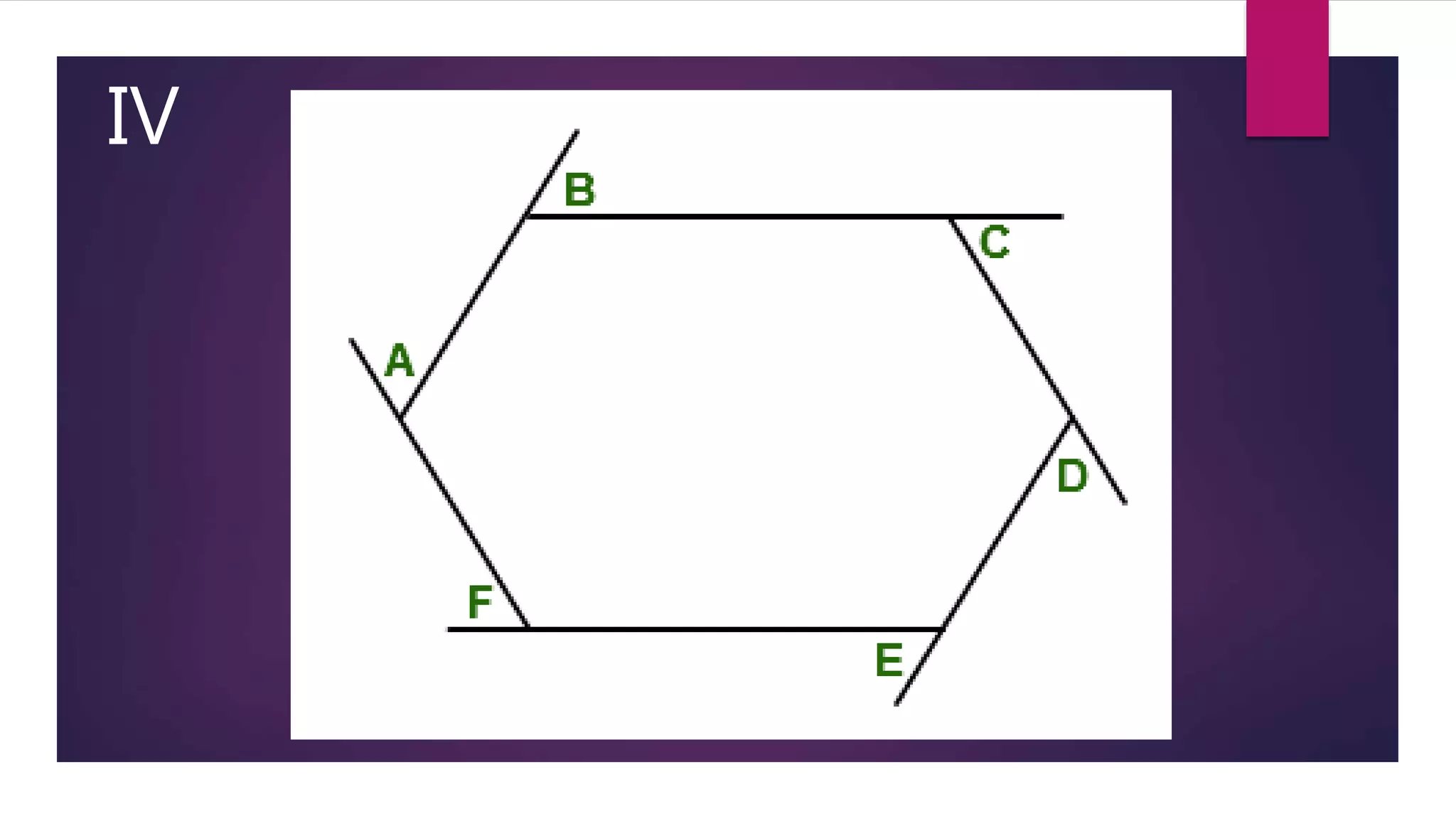












This document outlines an activity to verify that the sum of the measures of the exterior angles of any polygon is always 3600. The activity involves drawing examples of different polygons on glaze paper, extending the sides to form the exterior angles, cutting out the interior angles and rearranging them to form a full circle by joining them to the exterior angles. Through this process, it is observed that the exterior angles always sum to 3600 when rearranged, verifying the principle for polygons.




















