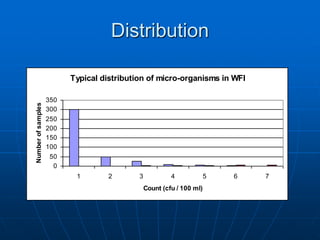
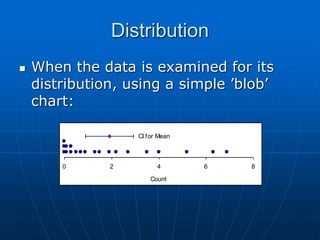
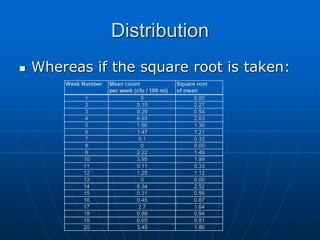
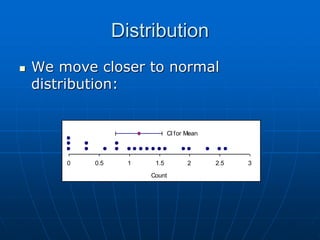
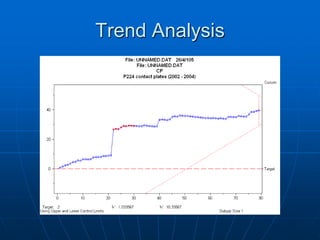
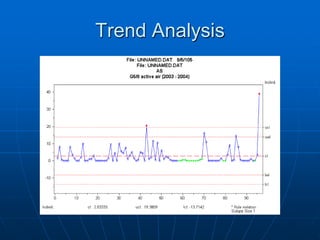
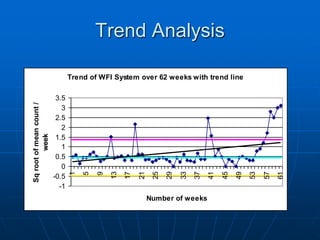
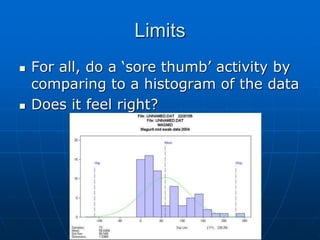
The document discusses the distribution and analysis of microbiological data, emphasizing that most such data does not follow a normal distribution and often requires transformation for proper interpretation. It outlines various statistical methods for trend analysis using control charts, such as cumulative sum and Shewhart charts, to monitor process variations and establish alert and action levels. The conclusion highlights the importance of understanding microbial distributions and emphasizes a professional approach to microbiology beyond mere numerical analysis.

1. Applications of
Microbiolgical Data
Tim Sandle
Microbiology information
resource:
http://www.pharmamicroresources.com/

2. Introduction
 Distribution of microbiological data
 Use of trend charts
 Calculation of warning and action
levels

3. Introduction
 Examples from environmental
monitoring and water testing
 Broad and illustrative overview
 Written paper with more detail

4. Distribution of microbiological data
 Why study distribution?
• Impact on sampling
• Impact on trending
• Impact upon calculation of warning and
action levels

5. Distribution
 Most statistical methods are based
on normal distribution, and yet….
 Most microbiological data does NOT
follow normal distribution

6. Distribution
 Micro-organisms, such as those in a
typical, free-flowing water system,
follow Poisson distribution
 For example…

7. Distribution
S1 S2 S3
S4 S5
Where S = sample
= micro-organism

8. Distribution
 And microbial counts tend to be
skewed (or positive or negative
exponential distribution)
 For example, a Water-for-Injection
system…

9. Distribution
Typical distribution of micro-organisms in WFI
0
50
100
150
200
250
300
350
1 2 3 4 5 6 7
Count (cfu / 100 ml)
Numberofsamples

10. Distribution
 So, what can we do about it?
Skewed question mark

11. Distribution
 Well:
a) Use complex calculations and
Poisson distribution tables, or
b) Attempt to transform then data
 We’ll go for the second option

12. Distribution
 A general rule is:
• For low count data e.g. Grade A
monitoring and WFI systems, take the
square root
• For higher count data, e.g. Grade C and
D environmental monitoring or a
purified water system, convert the data
into logarithms

13. Distribution
 For example, some counts from a
WFI system:

14. Distribution
 When the data is examined for its
distribution, using a simple ’blob’
chart:
CI for Mean
0 2 4 6 8
Count

15. Distribution
 Whereas if the square root is taken:

16. Distribution
 We move closer to normal
distribution:
CI for Mean
0 0.5 1 1.5 2 2.5 3
Count

17. Distribution
 Logarithms work in a similar way for
higher counts
 Remember to add ‘+1’ to zero counts
(and therefore, +1 to all counts)

18. Trend Analysis
 There is no right or wrong approach
 There are competing systems
 This presentation focuses on two
approaches, both described as
‘control charts’:
• The cumulative sum chart
• The Shewhart chart

19. Trend Analysis
 Control charts form part of the
quality system
 They can be used to show:
• Excessive variations in the data
• How variations change with time
• Variations that are ‘normally’ expected
• Variations that are unexpected, i.e.
something unusual has happened

20. Trend Analysis
 Control charts need:
• A target value, e.g. last year’s average
• Monitoring limits:
 Upper limit
 Lower limit
 Control line / mean
 So the data can be monitored over time and
in relation to these limits

21. Trend Analysis
 Of these,
• The warning limit is calculated to represent a
2.5% chance
• The action level is calculated to represent a
0.1% chance
• So, if set properly, most data should remain
below these limits
• These assumptions are based on NORMAL
DISTRIBUTION
• Various formula can be used to set these or
validated software

22. Trend Analysis
 Cumulative sum chart (cusum)
• Suitable for large quantities of low count
data. It is very sensitive to small shifts
• Shows shifts in the process mean
 Shewhart chart
• Suitable for higher count data. It shows
large changes more quickly.

23. Trend Analysis
 Cusums
• Harder to interpret
• Displays the cumulative sum of a rolling
average of three values and plots these
in comparison with the target value
• The direction and steepness of the slope
are important
• Significant changes are called ‘steps’
• V-masks can be used as a prediction to
the future direction

24. Trend Analysis
 For example, a Grade B cleanroom
 Contact (RODAC) plates are
examined
 A target of 0.2 cfu has been used,
based on data from the previous
year

25. Trend Analysis

26. Trend Analysis
 Shewhart charts
• Powerful for distinguishing between
special causes and common causes
• Common causes are inherent to the
process and are long-term
• Special causes are where something has
changed and maybe of a long or short
term

27. Trend Analysis
 Examples of special causes:
• a) A certain process
• b) A certain outlet
• c) A certain method of sanitisation, etc.
• d) Sampling technique
• e) Equipment malfunction e.g. pumps, UV
lamps
• f) Cross contamination in laboratory
• g) Engineering work
• h) Sanitisation frequencies

28. Trend Analysis
 For example, a Grade C cleanroom
• Active air-samples are examined
• A target of 1.5, based on historical data

29. Trend Analysis

30. Trend Analysis
 The previous charts were prepared
using a statistical software package
 However, MS Excel can also be used
 The next example is of a WFI system
 Notice the data has been converted
by taking the square root of each
value

31. Trend Analysis
Trend of WFI System over 62 weeks with trend line
-1
-0.5
0
0.5
1
1.5
2
2.5
3
3.5
1
5
9
13
17
21
25
29
33
37
41
45
49
53
57
61
Number of weeks
Sqrootofmeancount/
week

32. Trend Analysis
 Alternatives:
• Individual Value / Moving Range charts
• Exponentially Weighted Moving Average
charts (EWMA)
• These are useful where counts are NOT
expected, e.g. Grade A environments
• They look at the frequency of intervals
between counts

33. Trend Analysis
 Summary
Chart Type Advantage Disadvantage
Cumulative sum Cusum charts are more
sensitive to small process
shifts.
Large,
abrupt shifts are not
detected as fast as in a
Shewhart chart.
Shewhart chart Systematic shifts are
easily detected.
The probability of
detecting small shifts fast
is rather small

34. Limits
 Alert and action levels
 Based on PDA Tech. Report 13 (2001):
• Alert level: a level, when exceeded, indicates
that the process may have drifted from its
normal operating condition. This does not
necessarily warrant corrective action but
should be noted by the user.
• Action level: a level, when exceeded, indicates
that the process has drifted from its normal
operating range. This requires a documented
investigation and corrective action.

35. Limits
 Why use them?
• Assess any risk (which can be
defined as low, medium or high)
• To propose any corrective action
• To propose any preventative action

36. Limits
 “Level” is preferable to “Limit”
 Limits apply to specifications e.g.
sterility test
 Levels are used for environmental
monitoring

37. Limits
 Regulators set ‘guidance’ values e.g.
EU GMP; USP <1116>; FDA (2004)
 These apply to new facilities
 User is expected to set their own
based on historical data
• Not to exceed the published values
• Many references stating this
• Views of MHRA and FDA

38. Limits
 Things to consider:
• The length of time that the facility has been in
use for
• How often the user intends to use the limits for
(i.e. when the user intends to re-assess or re-
calculate the limits. Is this yearly? Two yearly?
And so on).
• Custom and practice in the user’s organisation
(e.g. is there a preferred statistical technique?)
• They be calculated from an historical analysis
of data.
• Uses a statistical technique.

39. Limits
 Historical data
• Aim for a minimum of 100 results
• Ideally one year, to account for
seasonal variations

40. Limits
 Statistical methods:
• Percentile cut-off
• Normal distribution
• Exponential distribution
• Non-parametric tolerance limits
• Weibull distribution
Recommended by PDA Technical
Report, No. 13

41. Limits
 Assumptions:
a) The previous period was ‘normal’
and that future excursions above the
limits are deviations from the norm
b) Outliers have been accounted for

42. Limits
 Percentile cut-off
• Good for low count data
• May need to use frequency tables
• May need to round up or down to
nearest whole zero or five
• Warning level = 90th or 95th
• Action level = 95th or 99th

43. Limits
 Percentile cut-off
• Data is collected, sorted and ranked
 90th percentile means that any future result
that exceeds this is 90% higher than all of
the results obtained over the previous year.
• Refer to PharMIG News Number 3
(2000) for excellent examples.

44. Limits
 Normal distribution
• Can only be used on data that is
normally distributed!
• Could transform data but inaccuracies
can creep in
• Most data will be one-tailed, therefore
need to adjust 2nd and 3rd standard
deviation
 Warning level = 1.645 + the mean
 Action level = 2.326 + the mean

45. Limits
 Negative exponential distribution
• Suitable for higher count data
• Warning level: 3.0 x mean
• Action level: 4.6 x mean

46. Limits
 For all, do a ‘sore thumb’ activity by
comparing to a histogram of the data
 Does it feel right?

47. Conclusion
 We have looked at:
• Distribution of microbiological data
• Trending
 Cusum charts
 Shewhart charts
• Setting warning and action levels
 Percentile cut-off
 Normal distribution approach
 Negative exponential approach

48. Conclusion
 Key points:
• Most micro-organisms and microbial
counts do not follow normal distribution
• Data can be transformed
• Inspectors expect some trending and
user defined monitoring levels
• Don’t forget to be professional
microbiologists – it isn’t all numbers!

49. Just a thought…
 This has been a broad over-view
 If there is merit in a more ‘hands on’
training course, please indicate on
your post-conference questionnaires.

50. Thank you