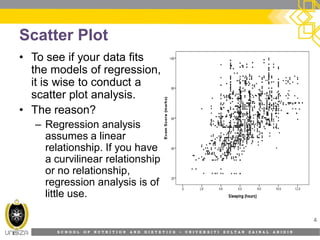
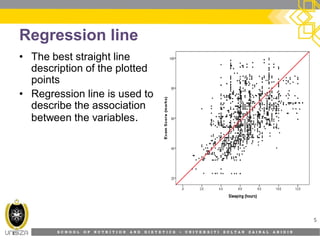
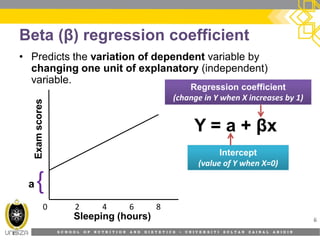
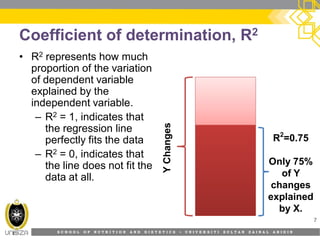
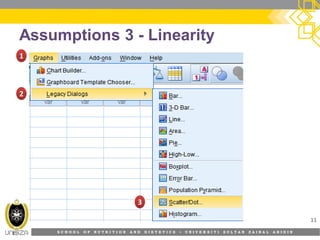
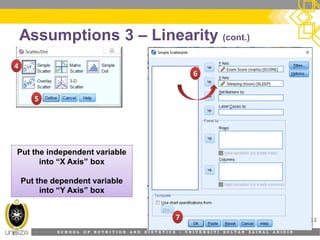
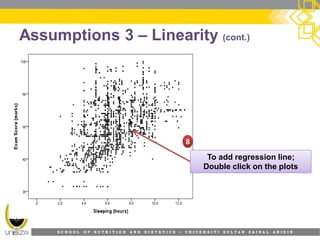
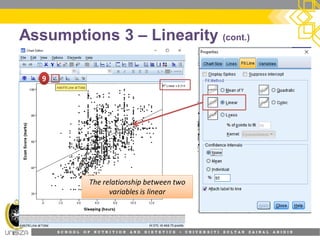
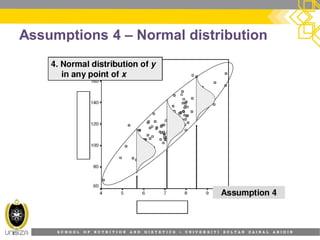
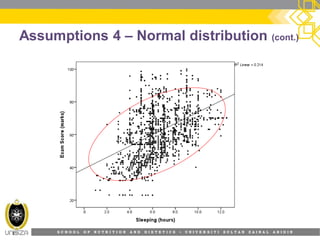
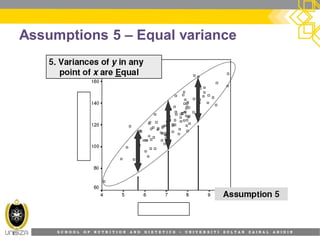
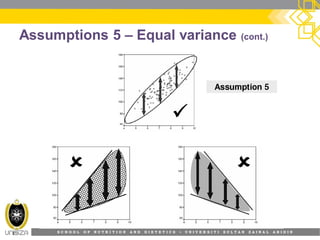
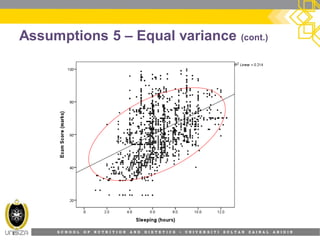
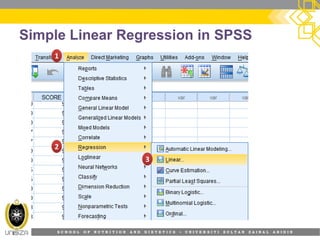
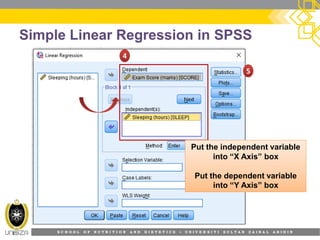
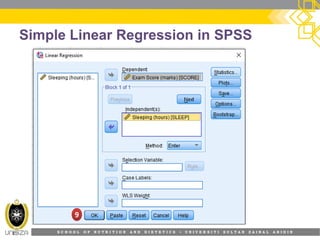
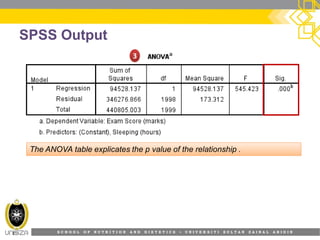
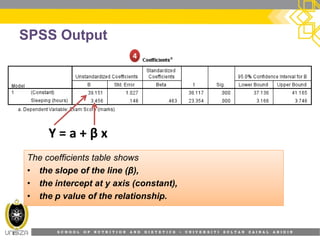
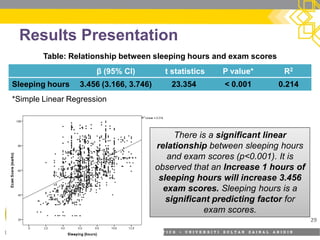
This document provides an overview of simple linear regression analysis. It discusses key topics like the regression line, coefficient of determination, assumptions of linear regression, and how to perform and interpret a simple linear regression in SPSS. The learning outcomes are to identify regression types, explain assumptions, perform regression in SPSS, and interpret the outputs. An example analyzing the relationship between sleeping hours and exam scores is used to demonstrate these concepts.

1. KNOWLEDGE FOR THE BENEFIT OF HUMANITYKNOWLEDGE FOR THE BENEFIT OF HUMANITY
BIOSTATISTICS (HFS3283)
REGRESSION
Dr.Dr. MohdMohd RazifRazif ShahrilShahril
School of Nutrition & DieteticsSchool of Nutrition & Dietetics
Faculty of Health SciencesFaculty of Health Sciences
UniversitiUniversiti SultanSultan ZainalZainal AbidinAbidin
1

2. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Topic Learning Outcomes
At the end of this lecture, students should be able to;
• identify types of regression analysis and their use.
• explain assumptions to be met when using Simple Linear
Regression.
• perform Simple Linear Regression analysis using SPSS.
• explain how to interpret the SPSS outputs from Simple
Linear Regression analysis.
2

3. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Regression
• Regression analysis is the estimation of linear
relationship between a dependent variable and one or
more independent variables or covariates
• Regression is used to predict the value of the dependent
variable when value of independent variable(s) known
• Does not imply causality
• Regression analysis requires interval and ratio-level
data.
3

4. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Scatter Plot
• To see if your data fits
the models of regression,
it is wise to conduct a
scatter plot analysis.
• The reason?
– Regression analysis
assumes a linear
relationship. If you have
a curvilinear relationship
or no relationship,
regression analysis is of
little use.
4

5. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Regression line
• The best straight line
description of the plotted
points
• Regression line is used to
describe the association
between the variables.
5

6. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Beta (β) regression coefficient
• Predicts the variation of dependent variable by
changing one unit of explanatory (independent)
variable.
6Sleeping (hours)
Examscores
0 2 4 6 8
Y = a + βx
Regression coefficientRegression coefficient
(change in Y when X increases by 1)
InterceptIntercept
(value of Y when X=0)
a{

7. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Coefficient of determination, R2
• R2 represents how much
proportion of the variation
of dependent variable
explained by the
independent variable.
– R2 = 1, indicates that
the regression line
perfectly fits the data
– R2 = 0, indicates that
the line does not fit the
data at all.
7
R2
=0.75
Only 75%
of Y
changes
explained
by X.
YChanges

8. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Types of regression analysis
• Simple Linear Regression
– 1 numerical variable (dependent) vs. 1 numerical variable
(independent)
• Multiple Linear Regression
– 1 numerical variable (dependent) vs. more than 1 numerical
variable (independent)
• Multivariable Linear Regression
– 1 numerical variable (dependent) vs. more than 1 numerical or
categorical variables (independent)
• Multivariate Linear Regression
– More than 1 numerical or categorical variables (dependent) vs.
more than 1 numerical or categorical variables (independent)
• Logistics Regression
– 1 categorical variable (dependent) vs. more than 1 numerical or
categorical variables (independent)
8

9. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Research Q’s and Hypothesis
Example;
• Research Question
– Is sleeping hours a predicting factor of exam scores?
• Null Hypothesis (Ho: β = 0)
– There is no linear relationship between the sleeping
hours and exam scores
• Alternate Hypothesis (Ha: β ≠ 0)
– There is a significant linear relationship between the
sleeping hours and exam scores
9

10. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Assumptions
• The data is drawn from a random sample of
population.
• The data is independent to each other.
• The relationship between two variables must be
linear.
• There is normal distribution of y at any point of
x.
• There is equal variance of y at any point of x.
10

11. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Assumptions 3 - Linearity
11
11
22
33

12. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Assumptions 3 – Linearity (cont.)
12
44
55
66
77
Put the independent variablePut the independent variable
into “X Axis” box
Put the dependent variable
into “Y Axis” box

13. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Assumptions 3 – Linearity (cont.)
To add regression line;To add regression line;
Double click on the plots
88

14. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Assumptions 3 – Linearity (cont.)
99
The relationship between twoThe relationship between two
variables is linear

15. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Assumptions 4 – Normal distribution

16. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Assumptions 4 – Normal distribution (cont.)

17. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Assumptions 5 – Equal variance

18. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Assumptions 5 – Equal variance (cont.)

19. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Assumptions 5 – Equal variance (cont.)

20. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Simple Linear Regression in SPSS
11
22
33

21. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Simple Linear Regression in SPSS
44
55
Put the independent variablePut the independent variable
into “X Axis” box
Put the dependent variable
into “Y Axis” box

22. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Simple Linear Regression in SPSS
66
88
77

23. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Simple Linear Regression in SPSS
99

24. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
SPSS Output
11
• The table demonstrates the method used in this data analysis.
•
• The table demonstrates the method used in this data analysis.
• No variable selection was carried out.

25. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
SPSS Output
22
The ‘Model Summary’ table shows the
•
•
•
•
•
The ‘Model Summary’ table shows the
• Correlation coefficient (R)
• Coefficient of determination (R2)
• The correlation coefficient (r) is 0.463 and thus there is fair
positive linear relationship between the two variable.
• The coefficient of determination (r2) is 0.214.
• Thus 21.4% of variation of exam scores is explained by sleeping
hours.

26. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
SPSS Output
33
The ANOVA table explicates the p value of the relationship .The ANOVA table explicates the p value of the relationship .

27. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
SPSS Output
44
The coefficients table shows
•
•
•
The coefficients table shows
• the slope of the line (β),
• the intercept at y axis (constant),
• the p value of the relationship.
Y = a + β x

28. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
SPSS Output Interpretation
• The slope of the regression line (β) is 3.456 with y axis
intercept at 39.151.
• Increase 1 hours of sleeping hours will increase
3.456 exam scores.
• The regression equation:
Exam scores = 39.151 + 3.456 (sleeping hours)
• The p value is < 0.05, therefore reject null hypothesis.
• There is a significant linear relationship between
sleeping hours and exam scores (p<0.001).
• Sleeping hours is a significant predicting factor for
exam scores.
28

29. S C H O O L O F N U T R I T I O N A N D D I E T E T I C S • U N I V E R S I T I S U L T A N Z A I N A L A B I D I N
Results Presentation
29
β (95% CI) t statistics P value* R2
Sleeping hours 3.456 (3.166, 3.746) 23.354 < 0.001 0.214
Table: Relationship between sleeping hours and exam scores
*Simple Linear Regression
There is a significant linear
between sleeping hours
observed that an of
There is a significant linear
relationship between sleeping hours
and exam scores (p<0.001). It is
observed that an Increase 1 hours of
sleeping hours will increase 3.456
exam scores. Sleeping hours is a
significant predicting factor for
exam scores.

30. Thank YouThank You
30